Хранение деревьев в таблицах

codedokode / Как хранить в БД древовидные структуры (паста).md

Древовидные структуры — это такие структуры, где есть родители и дети, например, каталог товаров:

Бытовая техника (id=1) Телевизоры (id=2) Плазменные (id=3) LCD (id=4) Холодильники (id=5) Маленькие (id=6) Средние (id=7) Большие (id=8) Профессиональная техника (id=9) . 

Типичные задачи, которые встречаются при работе с такими структурами:

• выбрать всех детей элемента
• выбрать всех потомков (детей и их детей) элемента
• выбрать цепочку предков элемента (родитель, его родитель, и так далее)
• переместить элемент (и его потомков) из одной группы в другую
• удалить элемент из таблицы (со всеми потомками)

У каждой записи есть идентификатор — уникальное число, он на схеме написан в скобках (думаю, это ты и так знаешь). Рассмотрим способы хранения таких данных.

1) Добавить колонку parent_id (метод Adjacency List)

Мы добавляем к каждой записи колонку parent_id (и индекс на нее), которая хранит id родительской записи (если родителя нет — NULL). Это самый простой, но самый неэффективный способ. Вот как будет выглядеть вышеприведенное дерево:

Бытовая техника (id=1, parent_id=NULL) Телевизоры (id=2, parent_id=1) Плазменные (id=3,parent_id=2) LCD (id=4,parent_id=2) Холодильники (id=5,parent_id=1) 

Выбрать всех детей просто: SELECT WHERE parent_id = ? , но другие операции требуют выполнения нескольких запросов и на больших деревьях особо неэффективны. Например, выбор всех потомков элемента с идентификатором :id

• выбрать список детей :id ( SELECT WHERE parent_id = :id )
• выбрать список их детей ( SELECT WHERE parent_id IN (:children1) )
• выбрать список детей детей ( SELECT WHERE parent_id IN (:children2) )

И так, пока мы не дойдем до самого младшего ребенка. После этого надо еще отсортировать и объединить результаты в дерево.

Плюсом, впрочем, является быстрая вставка и перемещение веток, которые не требуют никаких дополнительных запросов, и простота реализации. Если можно эффективно кешировать выборки, это в общем-то нормальный и работающий вариант (например, для меню сайта). Это может быть годный вариант для часто меняющихся данных.

Иногда еще добавляют поле depth , указывющее глубину вложенности, но его надо не забыть обновлять при перемещении ветки.

2) Closure table — усовершенствование предыдущего способа

В этом способы мы так же добавляет поле parent_id , но для оптимизации рекурсивных выборок создаем дополнительную таблицу, в которой храним всех потомков (детей и их детей) и их глубину относительно родителя каждой записи. Поясню. Дополнительная таблица выглядит так:

parent_id child_id depth 1 1 0 // Перечислены все дети записи с 2 1 1 3 2 1 4 2 1 5 1 . 2 2 0 2 3 1 2 4 1 

Чтобы узнать всех потомков записи, мы (в отличие от предыдущего способа), делаем запрос к дополнительной таблице: SELECT child_id FROM closure_table WHERE parent_id = :id , получаем id потомков и выбираем их их основной таблицы: SELECT WHERE id IN (:children) . Если таблицы хранятся в одной БД, запросы можно объединить в один с использованием JOIN.

Данные потом надо будет вручную отсортировать в дерево.

Узнать список предков можно тоже одним запросом к таблице связей: SELECT parent_id FROM closure_table WHERE child_id = :id ORDER BY depth

Минусы метода: нужно поддерживать таблицу связей, она может быть огромной (размер посчитайте сами), при вставке новых записей и при перемещении веток нужны сложные манипуляции. Если таблица часто меняется, это не лучший способ.

Плюсы: относительная простота, быстрота выборок.

Идея в том, что мы добавляем к каждой записи поля parent_id , depth , left , right и выстраиваем записи хитрым образом. После этого выборка всех потомков (причем уже отсортированных в нужном порядке) делаетсяпростым запросом вида SELECT WHERE left >= :a AND right

Минусы: необходимость пересчитывать left / right при вставке записей в середину или удалении, сложное перемещение веток, сложность в понимании.

В общем-то, годный вариант для больших таблиц, которые часто выбираются, но меняются нечасто (например, только через админку, где не критична производительность).

Идея в том, что записи в пределах одной ветки нумеруются по порядку и в каждую запись добавляется поле path, содержащее полный список родителей. Напоминает способ нумерации глав в книгах. Пример:

Бытовая техника (id=1, number=1, path=1) Телевизоры (id=2, number=1, path=1.1) Плазменные (id=3, number=1, path=1.1.1) LCD (id=4, number=2, path=1.1.2) Холодильники (id=5, number=2, path=1.2) 

При этом способе path хранится в поле вроде TEXT или BINARY, по нему делается индекс. Выбрать всех потомков можно запросом SELECT WHERE path LIKE ‘1.1.%’ ORDER BY path , который использует индекс.

Плюс: записи выбираются уже отсортированными в нужном порядке. Простота решения и скорость выборок высокая (1 запрос). Быстрая вставка.

Минусы: при вставке записи в середину надо пересчитывать номера и пути следующих за ней. При удалении ветки, возможно тоже. При перемещении ветки надо делать сложные расчеты. Глубина дерева и число детей у родителя ограничены выделенным дял них местом и длиной path

Этот способ отлично подходит для древовидных комментариев.

5) Использовать БД с поддержкой иерархии

Я в этом не разбираюсь, может кто-то расскажет, какие есть возможности в БД для нативной поддержки деревьев. Вроде что-то такое есть в MSSQL и Oracle. Только хотелось бы услышать, как именно это оптимизируется и какой метод хранения используется, а не общие слова.

Источник

Хранение деревьев в базе данных. Часть первая, теоретическая

Полгода назад написал бандл ClosureTable для фреймворка Laravel 3. Поводом для написания стала вот эта замечательная презентация Билла Карвина о способах хранения и обработки иерархических данных в MySQL с использованием PHP.

• Adjacency List («список смежности»)
• Materialized Path («материализованный путь»)
• Nested Sets («вложенные множества»)
• Closure Table («таблица связей»)

Что такое Closure Table

Суть данного шаблона проектирования заключается в том, что связи между сущностями хранятся в отдельной таблице, тогда как основная таблица содержит только данные самих сущностей.

Таблица связей должна содержать как минимум два поля:

• ссылку на предка (ancestor)
• ссылку на потомка (descendant)

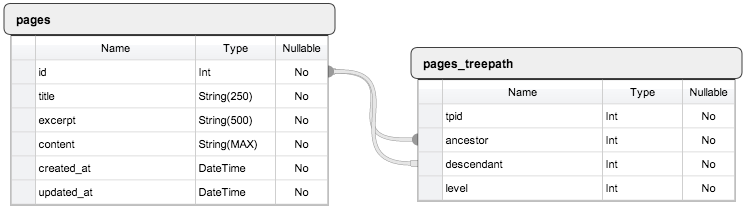
Пусть мы работаем над созданием очередной SuperPuper CMS и приступили к разработке модуля редактирования текстовых страниц. Нам понадобятся две таблицы:

• pages будет содержать данные о странице
• pages_treepath будет содержать данные об иерархии страниц

Схема таблиц БД

В качестве примера используем следующую иерархию страниц:

Выборка потомков

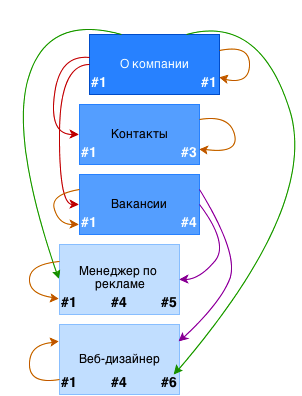
Вот такой SQL-запрос у нас получится, если мы захотим выбрать все страницы раздела «О компании».

SELECT * FROM pages p JOIN pages_treepath t ON (p.id = t.descendant) WHERE t.ancestor = 1 

Ветка полученного результата. Стрелки указывают на связи между страницами

«Descendant» означает «потомок», а «ancestor» — предок. Соответственно, чтобы получить все дочерние страницы, мы присоединяем таблицу связей pages_treepath при условии, что идентификатор страницы id имеет то же значение, что и ссылка на потомка descendant . При этом ссылка ancestor на родительскую страницу равняется 1 , идентификатору страницы «О компании».

Выборка предков

А теперь снизу вверх: посмотрим всех «родителей» у страницы «Корпоративный».

SELECT * FROM pages p JOIN pages_treepath t ON (p.id = t.ancestor) WHERE t.descendant = 11 

В этом случае наоборот. Мы ищем страницы выше по иерархии, поэтому присоединяем таблицу связей с условием, что идентификатор страницы id должен равняться ссылке на предка ancestor , а выборку осуществляем по ссылке на потомка descendant , в нашем случае равной 11 .

Вставка нового элемента

Можно добавить новую вакансию. Данные ценности в нашем случае не представляют, так что посмотрим на сам запрос.

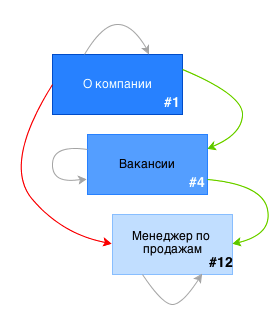
INSERT INTO pages VALUES (12, 'Менеджер по продажам', '', 'Требуется офигенный менеджер по продажам', '0000-00-00 00:00:00', '0000-00-00 00:00:00') INSERT INTO pages_treepath (ancestor, descendant) SELECT ancestor, 12 FROM pages_treepath WHERE descendant = 4 UNION ALL SELECT 12, 12 

С первым запросом все ясно — это простая вставка новых данных. А вот второй запрос стоит разобрать по порядку, так что давайте посмотрим, что тут происходит.

Связи между элементами после вставки новой вакансии

SELECT ancestor, 12 FROM pages_treepath WHERE descendant = 4 

------------------------- | ancestor | descendant | ------------------------- | 4 | 12 | | 1 | 12 | -------------------------

Добавим к предыдущему запросу еще один путем объединения:

SELECT ancestor, 12 FROM pages_treepath WHERE descendant = 4 UNION ALL SELECT 12, 12 

------------------------- | ancestor | descendant | ------------------------- | 4 | 12 | | 1 | 12 | | 12 | 12 | -------------------------

Как видите, данный SELECT-запрос позволяет установить связи между новой страницей и всеми её предками. ancestor — всегда ссылка на предка, descendant — ссылка на потомка. INSERT-запрос, написанный вначале, вставляет полученный результат в таблицу pages_treepath .

Удаление элемента

А теперь закроем вакансию веб-дизайнера.

DELETE FROM pages_treepath WHERE descendant = 6 DELETE FROM pages WHERE > Здесь всё просто. Сначала мы удаляем все связи, где ссылка на потомка равняется 6 (страница «Веб-дизайнер»), а затем удаляем и саму страницу.

Удаление вложенного дерева

Вдруг так случилось, что с некоторых пор компания ABC перестала разрабатывать сайты. Нам понадобится выполнить вот такой запрос, чтобы удалить соответствующий подраздел:

DELETE FROM pages WHERE id IN ( SELECT descendant FROM ( SELECT descendant FROM pages p JOIN pages_treepath t ON p.id = t.descendant WHERE t.ancestor = 7 ) AS tmptable ) DELETE FROM pages_treepath WHERE descendant IN ( SELECT descendant FROM ( SELECT descendant FROM pages_treepath WHERE ancestor = 7 ) AS tmptable ) 

В отличие от предыдущего запроса, этот несколько сложнее и сначала удаляются сами страницы и уже после этого связи между ними (поскольку последние активно используются при удалении первых).

Сложность запросов отчасти объясняется тем, что MySQL не позволяет выполнять запрос на удаление записей с условием WHERE , в котором содержится выборка SELECT из той же таблицы. В случае с MySQL мы вынуждены поместить SELECT-запросы во временную таблицу. А в общем случае наши запросы выглядели бы так:

DELETE FROM pages WHERE id IN ( SELECT descendant FROM pages p JOIN pages_treepath t ON p.id = t.descendant WHERE t.ancestor = 7 ) DELETE FROM pages_treepath WHERE descendant IN ( SELECT descendant FROM pages_treepath WHERE ancestor = 7 ) 

Если вы внимательно посмотрите на вложенный SELECT-запрос в DELETE-запросе из таблицы pages , то обнаружите, что мы уже рассматривали подобный запрос. Этот от предыдущего отличается только идентификатором страницы. В результате выборки мы получаем все дочерние страницы раздела «Сайты» (включая сам раздел), а затем удаляем все страницы с полученными идентификаторами.

После того, как страницы удалены, остаётся удалить связи между ними. Для этого находим все ссылки на потомков descendant , где ссылка на предка равняется идентификатору страницы «Сайты».

Уровень вложенности

Еще в таблицу связей можно добавить поле, контролирующее уровень вложенности элементов. Это поле позволит составлять более простые запросы на выборку непосредственных предков или непосредственных потомков. Например:

SELECT * FROM pages p JOIN pages_treepath t ON (p.id = t.descendant) WHERE t.ancestor = 4 AND t.level = 2 

Схема таблиц БД

Источник