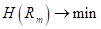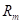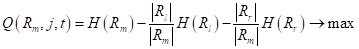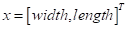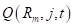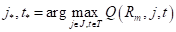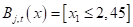Машинное обучение 101-ID3 Деревья принятия решений и вычисление энтропии (1)
Энтропия, известная как контроллер дерева решений, решающая, где разделить данные. Алгоритм ID3 использует энтропию для вычисления однородности образца. Если образец полностью однороден, энтропия равна нулю, а если образец разделен поровну, он имеет энтропию, равную единице [1].
Энтропия n-класса — ›E (S) = ∑ — (pᵢ * log₂pᵢ)
2-х классная энтропия: (S) = — (p₁ * log₂p₁ + p₂ * log₂p₂)
Ex-1:
p₁ = 9 / (9 + 5) = 9/14 (вероятность попадания выборки в один обучающий класс с классом 1)
p₂ = 5/14 (вероятность попадания образца в один учебный класс с классом 2)
E = — (9/14 * log₂ (9/14) + (5/14) * log₂ (5/14))
Получение информации
Границы корня, узлов и листьев определяются приростом информации (IG).
Усиление (S, A) = E (до) — G (после_разбиения)
Примечание. Вы можете найти ID3 как C4.5 в WEKA Tool.
Сначала выберите функцию, которая наиболее точно разделит всю таблицу. Для этого необходимо определить функцию, которая дает наибольший выигрыш.
Значения для 10 примеров тренировок делятся следующим образом:
* 6 Кино
* 2 Теннис
* 1 Хаус * 1 Покупки
Значение энтропии должно быть рассчитано на основе этих значений для начала определения корневого объекта.
E (S) = — ((6/10) * log2 (6/10) + (2/10) * log2 (2/10) + (1/10) * log2 (1/10) + (1/10 ) * log2 (1/10))
Вычисляя значения усиления для всех отдельных объектов, объекты с наибольшим значением усиления выбираются в качестве корневого узла:
Прирост (S, Погода) =?
Солнечный = 3 (1 кино + 2 теннис)
Windy = 4 (3 кинотеатра + 1 покупка)
Rainy = 3 (2 кинотеатра + 1 дом)
Энтропия (S солнечный) = — (1/3) * log2 (1/3) — (2/3) * log2 (2/3) = 0,918
Энтропия (S ветрено) = — (3/4) * log2 (3/4) — (1/4) * log2 (1/4) = 0,811
Энтропия (S дождливый) = — (2/3) * log2 (2/3) — (1/3) * log2 (1/3) = 0,918
Прирост (S, Погода) = 1,571 — (((1 + 2) / 10) * 0,918 + ((3 + 1) / 10) * 0,811 + ((2 + 1) / 10) * 0,918)
Прирост (S, Погода) = 0,70
Gain (S, Parental_Availability) =?
Нет = 5 (2 тенниса + 1 кинотеатр + 1 магазин + 1 дом)
Энтропия (S да) = — (5/5) * log2 (5/5) = 0
Энтропия (S нет) = — (2/5) * log2 (2/5) -3 * (1/5) * log2 (1/5) = 1,922
Прирост (S, родительская_доступность) = энтропия (S) — (P (да) * энтропия (S да) + P (нет) * энтропия (S нет))
Прирост (S, родительская_доступность) = 1,571 — ((5/10) * энтропия (S да) + (5/10) * энтропия (S нет))
Прирост (S, родительская_доступность) = 0,61
Богатые = 7 (3 кинотеатра + 2 тенниса + 1 магазин + 1 дом)
Прирост (S, богатство) = энтропия (S) — (P (богатый) * энтропия (S богатый) + P (бедный) * энтропия (S бедный))
Прирост (S, богатство) = 0,2816
Наконец, все значения усиления перечисляются одно за другим, и в качестве корневого узла выбирается объект с наибольшим значением усиления. В этом случае погода имеет наибольшее значение усиления, поэтому она будет корнем.
Прирост (S, Погода) = 0,70
Прирост (S, Родительская_доступность) = 0,61
Прирост (S, богатство) = 0,2816
Как показано в приведенном выше примере, после выбора корня каждое из отдельных значений функций определяется как листья, и на этот раз набор данных настраивается с этими отдельными значениями. Другими словами, приведенная выше таблица была преобразована в отдельный набор данных, показывающий значения, которые могут принимать другие функции, если погода солнечная. Таким образом, при солнечной погоде, согласно этой таблице, возможные классы интер узла будут следующими:
Энтропия (S солнечный) = — (1/3) * log2 (1/3) — (2/3) * log2 (2/3) = 0,918
Усиление (S солнечно, Parental_Availability) =?
Прирост (S солнечно, Parental_Availability) = энтропия (S солнечно) — (P (да | S солнечно) * энтропия (S да) + P (нет | S солнечно) * энтропия (S нет))
Энтропия (S да) = — (1/3) * log2 (0) — 0 = 0
Энтропия (S нет) = — (2/3) * log2 (0) — 0 = 0
Прирост (S солнечно, Родительская_доступность) = 0,928 — ((1/3) * 0 + (2/3) * 0) = 0,928
Прирост (S солнечно, богатство) = 0,918 — ((3/3) * 0,918 + (0/3) * 0) = 0
Поскольку усиление функции Parental_Availability больше, лист состояния Sunny будет Parental_Availability. В соответствии с набором данных для солнечных условий, если да, будет выбрано Кино, а если нет, то будет выбрано Теннис:
Когда те же расчеты будут выполнены для ветреной и дождливой ситуаций, окончательное дерево решений будет завершено.
Переоснащение
- Это превращение обучения в запоминание.
- График производительности таков, что через определенный момент прирост производительности прекращается и начинает уменьшаться.
- Когда у вас высокий уровень успешности тренировок, но наоборот — результативность тестов, это пример переобучения.
- Более того, если в наших данных есть зашумленная выборка, это может привести к переобучению.
- Когда дерево становится слишком большим, результат получается почти для каждой возможной ветви, что приводит к переоснащению.
Чтобы избежать переобучения, необходимо обрезать дерево либо когда оно растет, либо после того, как дерево сформируется.
Источник
Построение решающих деревьев жадным алгоритмом ID3
На предыдущем занятии мы с вами познакомились с критериями выбора предикатов для разбиения множества данных в вершинах решающего дерева. В первую очередь – это impurity (информативность, мера неопределенности), обозначим ее через
где — выборка, попавшая в текущую вершину. И показатель качества разбиения, который часто вычисляется как информационный выигрыш:
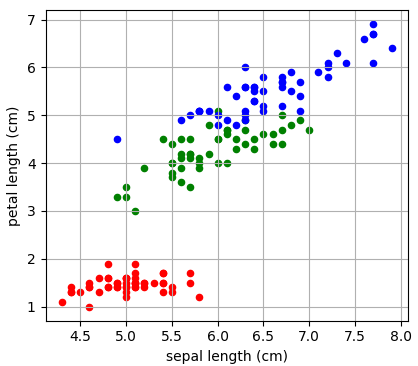
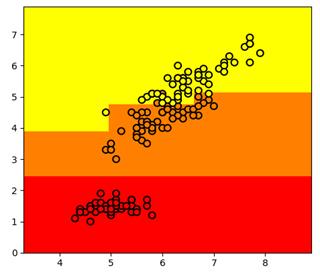
Давайте теперь воспользуемся этими показателями для построения бинарного решающего дерева. В качестве обучающей выборки возьмем 150 объектов трех классов ирисов (50 в каждом классе), распределенных в двумерном признаковом пространстве: длина и ширина лепестков:
То есть, входные векторы будут иметь два числовых признака:
Существует несколько распространенных алгоритмов построения решающих деревьев. Вначале я рассмотрю самый простой, который называется ID3 (Iterative Dichotomiser 3), разработанный Россом Куинланом в 1986 году для задачи классификации. Этот алгоритм использует энтропию в качестве информативности и реализует жадную стратегию, то есть, в каждом узле дерева, начиная с корневого, находит такой признак j и такой порог t, которые дают наибольшее значение показателя :
Затем, построение рекурсивно повторяется для каждой новой вершины.
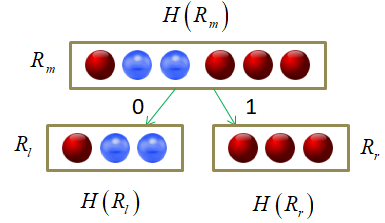
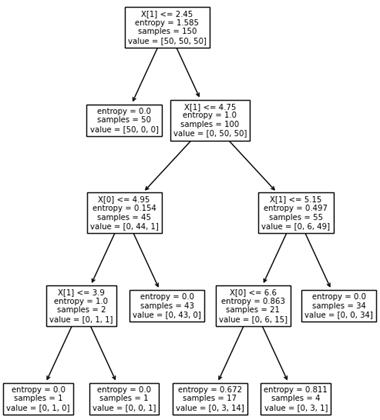
Вот пример разбиения обучающего множества деревом глубиной 4. Само дерево имеет вид:
Отсюда хорошо видно, как происходило разбиение. Вначале были отделены все красные объекты выборки по второму признаку (длина лепестка) с порогом t = 2,45 и предикатом:
Если предикат выполняется, то попадаем в листовую вершину с нулевой энтропией и 50-ю представителями класса «красных» объектов. Во вторую вершину попадает 100 объектов двух других классов с энтропией, равной 1. Далее, мы делим объекты второй вершины дерева также по второму признаку и уровню 4,75. Формируются следующие две вершины. И так далее, пока либо не будет достигнута нулевая энтропия и сформирован лист дерева, либо глубина дерева достигнет уровня 4. (Этот максимальный уровень был задан при генерации данного решающего дерева.) В каждой листовой вершине мы сохраняем метку класса с наибольшим числом представителей.
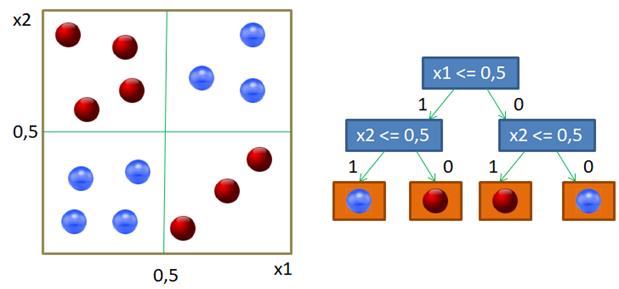
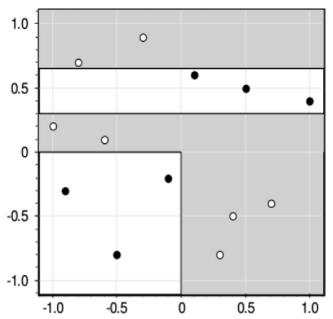
Вот наглядный пример работы жадного алгоритма ID3. Казалось бы, все прекрасно и ничто не мешает нам использовать его в самых разных задачах. Однако, практика показала, что жадная стратегия построения деревьев часто не самая лучшая. Простой контрпример – задача XOR, когда объекты двух классов сосредоточены в разных углах квадрата:
Жадная стратегия дает, следующее решающее дерево:
Но, тем не менее, алгоритм ID3 относительно прост в реализации, а потому является основой для более сложных подходов к построению решающих деревьев, о которых мы поговорим на следующих занятиях.
Критерии останова (методы регуляризации)
- impurity равна нулю или меньше некоторого заданного значения;
- число объектов в вершине меньше заданной величины;
- вероятность правильной классификации объекта больше заданной величины;
- достигнуто максимальное количество листьев в дереве;
- достигнута максимальная заданная глубина дерева.
Преимущества и недостатки жадной стратегии
Итак, я думаю, в целом идея построения решающих деревьев по алгоритму ID3 вам понятна. В заключение отмечу преимущества и недостатки такого подхода.
Достоинства:
- Интерпретируемость и простота классификации (легко объяснить результат классификации эксперту).
- Допустимы разнотипные данные и пропуски в данных.
- Не бывает отказов от классификации.
Недостатки:
- Жадная стратегия в большинстве задач излишне усложняет структуру дерева, то есть, приводит к его переобучению.
- Чем дальше от корня дерева, тем меньше объектов в листовых вершинах, а значит, ниже статистическая надежность различных показателей, например, вероятности появления того или иного класса.
- Высокая чувствительность к шуму в объектах выборки и критерию информативности (impurity).
Источник