Gini Index: Decision Tree, Formula, and Coefficient
Decision trees are often used while implementing machine learning algorithms. The hierarchical structure of a decision tree leads us to the final outcome by traversing through the nodes of the tree. Each node consists of an attribute or feature which is further split into more nodes as we move down the tree. But how do we decide:
- Which attribute/feature should be placed at the root node?
- Which features will act as internal nodes or leaf nodes?
To decide this, and how to split the tree, we use splitting measures like Gini Index, Information Gain, etc. In this blog, we will learn all about the Gini Index, including the use of Gini Index to split a decision tree.
Find it all out with this blog which covers:
Offered by Dr. Ernest Chan, learn to predict markets and find trading opportunities using AI techniques
What is Gini Index?
Gini Index or Gini impurity measures the degree or probability of a particular variable being wrongly classified when it is randomly chosen.
But what is actually meant by ‘impurity’?
If all the elements belong to a single class, then it can be called pure. The degree of Gini Index varies between 0 and 1,
where,
‘0’ denotes that all elements belong to a certain class or there exists only one class (pure), and
‘1’ denotes that the elements are randomly distributed across various classes (impure).
A Gini Index of ‘0.5 ‘denotes equally distributed elements into some classes.
Terms similar to Gini Index for execution of decision tree technique
We are discussing the components similar to Gini Index so that the role of Gini Index is even clearer in execution of decision tree technique.
The very essence of decision trees resides in dividing the entire dataset into a tree-like vertical information structure so as to divide the different sections of the information with root nodes at the top.
In the decision tree model, each node is an attribute or the feature that contains necessary information (going sequentially downward) for the decision tree model. These are the necessary points to keep in mind while deciding each node of the decision tree model:
- Which features are to be located at the root node from where the decision tree will begin. This information at the root node should be the base of the entire information going forward. For instance, if we are going to create the decision tree model for a stock, we could mention the data (OHLCV) of the stock at the root node.
- Deciding which are the most accurate features to serve as the internal nodes (going vertically down the tree), also known as the leaf nodes.
Coming to the other terms that also lead to the execution of the decision tree technique, similar to the Gini Index, these are as follows:
Create a machine learning trading strategy using Decision Trees and ensemble methods
Splitting measures
With more than one attribute taking part in the decision-making process, it is necessary to decide the relevance and importance of each of the attributes. Thus, placing the most relevant feature at the root node and further traversing down by splitting the nodes.
As we move further down the tree, the level of impurity or uncertainty decreases, thus leading to a better classification or best split at every node. Splitting measures such as Information gain, Gini Index, etc. are used to decide the same.
Information gain
Information gain is used to determine which feature/attribute gives us the maximum information about a class.
- Information gain is based on the concept of entropy, which is the degree of uncertainty, impurity or disorder.
- Information gain aims to reduce the level of entropy starting from the root node to the leaf nodes.
Relevance of Entropy
Entropy is a measure of the disorder or the measure of the impurity in a dataset. The Gini Index is a tool that aims to decrease the level of entropy from the dataset.
In other words, entropy is the measurement of the impurity or, we can say, randomness in the values of the dataset.
A low disorder (no disorder) implies a low level of impurity. Entropy is calculated between 0 and 1. The number “1” signifies a higher level of disorder or more impurity.
Although there can be other numbers of groups or classes present in the dataset that can be greater than 1. In the case of machine learning (and decision trees), 1 signifies the same meaning, that is, the higher level of disorder and also makes the interpretation simple. Hence, the decision tree model will classify the greater level of disorder as 1.
Entropy is usually the lowest disorder (no disorder) means a low level of impurity and higher disorder (maximum disorder) means there is a high level of impurity. The entropy is measured to reduce the uncertainty that comes with more impurity.
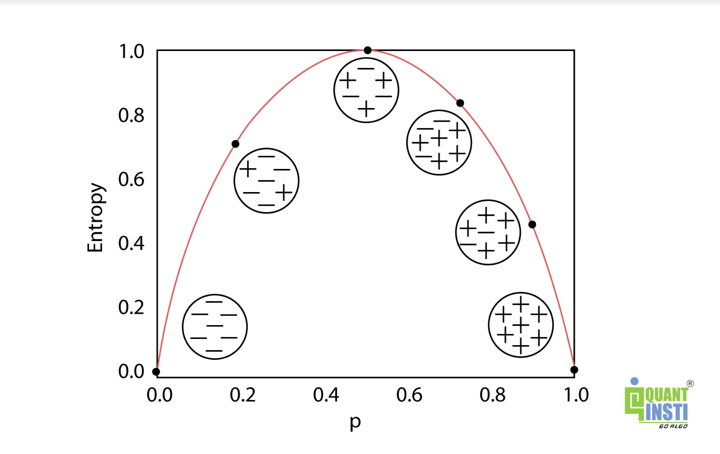
In the image below, you can see an inverted “U” shape representing the variation of entropy in the graph. In the image, the x-axis represents the data values and the y-axis represents the value of entropy.
Offered by Dr. Ernest Chan, learn to predict markets and find trading opportunities using AI techniques
The graph above shows that the entropy is the lowest (no disorder) at two extremes (both left and right sides) and maximum (high disorder) in the middle of the graph or at the curve of the inverted “U” shape.
Therefore, at both extremes (left and right), there is no entropy (impurity) as each class has all the elements that belong to that class. On the other hand, in the middle, the entropy line stretches to the highest point to create a “U” shape where all the elements from two classes are randomly distributed which means there is entropy (impurity).
It is clear from our observation that both the extremes (left and right) are pure with no entropy.
Formula for Entropy
The formula for entropy, in order to find out the uncertainty or the high disorder, goes as follows:
where,
‘p’, denotes the probability of entropy and E(S) denotes the entropy.
Formula of Gini Index
The formula of the Gini Index is as follows:
where,
‘pi’ is the probability of an object being classified to a particular class.
While building the decision tree, we would prefer to choose the attribute/feature with the least Gini Index as the root node.
Example of Gini Index
Let us now see the example of the Gini Index for trading. We will make the decision tree model be given a particular set of data that is readable for the machine.
Now, let us calculate Gini Index for past trend, open interest, trading volume and return in the following manner with the example data:
Источник
ML | Gini Impurity and Entropy in Decision Tree
Machine Learning is a Computer Science domain that provides the ability for computers to learn without being explicitly programmed. Machine Learning is one of the most highly demanded technologies that everybody wants to learn and most companies require highly skilled Machine Learning engineers. In this domain, there are various machine learning algorithms developed to solve complex problems with ease. These algorithms are highly automated and self-modifying, as they continue to improve over time with the addition of an increased amount of data and with minimum human intervention required. To learn about top Machine Learning algorithms that every ML engineer should know click here.
In this article, we will be focusing more on Gini Impurity and Entropy methods in the Decision Tree algorithm and which is better among them.
Decision Tree is one of the most popular and powerful classification algorithms that we use in machine learning. The decision tree from the name itself signifies that it is used for making decisions from the given dataset. The concept behind the decision tree is that it helps to select appropriate features for splitting the tree into subparts and the algorithm used behind the splitting is ID3. If the decision tree build is appropriate then the depth of the tree will be less or else the depth will be more. To build the decision tree in an efficient way we use the concept of Entropy. To learn more about the Decision Tree click here. In this article, we will be more focused on the difference between Gini Impurity and Entropy.
- The word “entropy,” is hails from physics, and refers to an indicator of the disorder. The expected volume of “information,” “surprise,” or “uncertainty” associated with a randomly chosen variable’s potential outcomes is characterized as the entropy of the variable in information theory.
- Entropy is a quantifiable and measurable physical attribute and a scientific notion that is frequently associated with a circumstance of disorder, unpredictability, or uncertainty.
- From classical thermodynamics, where it was originally identified, through the macroscopic portrayal of existence in statistical physics, to the principles of information theory, the terminology, and notion are widely used in a variety of fields of study
As discussed above entropy helps us to build an appropriate decision tree for selecting the best splitter. Entropy can be defined as a measure of the purity of the sub-split. Entropy always lies between 0 to 1. The entropy of any split can be calculated by this formula.
The internal working of both methods is very similar and both are used for computing the feature/split after every new splitting. But if we compare both methods then Gini Impurity is more efficient than entropy in terms of computing power. As you can see in the graph for entropy, it first increases up to 1 and then starts decreasing, but in the case of Gini impurity it only goes up to 0.5 and then it starts decreasing, hence it requires less computational power. The range of Entropy lies in between 0 to 1 and the range of Gini Impurity lies between 0 to 0.5. Hence we can conclude that Gini Impurity is better as compared to entropy for selecting the best features.
Difference between Gini Index and Entropy
Formula for the Gini index is Gini(P) = 1 – ∑(Px)^2 , where Pi is
the proportion of the instances of class x in a set.
Conclusion: It ought to be emphasized that there is no one appropriate approach for evaluating unpredictability or impurities, and that the decision between the Gini index and entropy varies significantly on the particular circumstance and methodology being employed.

Like Article
Источник