Информационное дерево представляет собой
На этом шаге мы рассмотрим сложность операций с бинарными деревьями .
Бинарные деревья часто используются для хранения информации. Они выгодно отличаются от массивов фиксированного размера своим динамическим характером, возможностью почти неограниченно увеличивать объемы хранимой информации. От линейных списков их отличают лучшие временные характеристики — например, при поиске элемента (наиболее часто используемой операции) требуется в среднем просмотреть меньшую часть дерева, чем это требовалось бы для списка с таким же количеством элементов. Проведем детальный анализ функций сложности этих операций.
Прежде всего определим, какой параметр можно рассматривать в качестве параметра V сложности данных. Наиболее очевидным кандидатом на эту роль является текущее количество n вершин в дереве. Но ясно, что величина n не определяет однозначно сложность. Есть хорошие и плохие деревья. Оценим с этой точки зрения параметр n — насколько при одном и том же значении n для разных деревьев могут отличаться функции сложности одной из самых простых операций — вставки нового элемента.
Условия анализа будут следующими: включаемый элемент является новым, т. е. элемента с таким значением информационного поля еще нет в дереве; рассматриваются два вида деревьев — идеальное, имеющее n = 2 k -1 вершин, и вырожденное (линейный список).
- новый элемент предшествует уже имеющимся, т. е. значение его информационного поля меньше значений информационных полей имеющихся в дереве вершин, в том числе корня; тогда новый элемент становится левым потомком корня, операция заканчивается за один шаг, дерево перестает быть вырожденным;
- все имеющиеся в дереве элементы предшествуют новому; новый элемент должен стать правым потомком последней (самой правой) вершины, для этого требуется выполнить n элементарных шагов; дерево остается вырожденным;
- новый элемент предшествует части вершин дерева, но другая часть вершин предшествует ему; в этом случае в списке имеется i -я вершина, левым потомком которой становится новый элемент; требуется выполнить i, 1
В случае (в) максимальная оценка сложности равна n , а средняя зависит от того, каким является множество, из которого выбираются значения информационных полей элементов, какое распределение имеет выборка из n значений, уже помещенных в дерево, и каково вероятностное распределение, из которого было выбрано значение информационного поля нового элемента. За неимением подробных сведений об этом обычно берут среднюю оценку в виде (n+1)/2 .
Таким образом, получаем оценки от log 2 (n+1) для лучших деревьев до n для худших деревьев при одинаковом количестве вершин n . Ясно, что максимальная оценка сложности включения элемента в произвольное дерево определяется худшим случаем. Со средней оценкой дело обстоит иначе. Усреднение должно быть произведено не только по характеристикам вновь включаемого элемента (как в случае «в»), но и по всевозможным деревьям. Поэтому следующим этапом является анализ того, как часто встречаются хорошие и плохие деревья.
- информационное поле искомого элемента имеет значение, заведомо отсутствующее в дереве, так называемый неудачный поиск ;
- искомый элемент присутствует в дереве, так называемый удачный поиск .
В первом случае количество сравнений такое же, как и при включении нового элемента, т. е. k , а количество переходов на единицу меньше.
Второй случай требует более подробного анализа. Предположим, что искомая вершина с равной вероятностью находится в любой из позиций идеального дерева. Время ее поиска однозначно определяется номером уровня, на котором эта вершина находится. Если это 1-й уровень (корень), то достаточно одного сравнения, если k -й уровень (одна из висячих вершин), то требуется максимальное количество сравнений — k . Таким образом, количество сравнений с n является случайной величиной, принимающей значения из интервала [1, k] . Осталось выяснить, какова вероятность p i , того, что с n примет значение i .
Очевидно, что, приняв условие равновероятности вершин при поиске, необходимо сделать вывод: вероятность попадания на некоторый уровень пропорциональна количеству вершин на этом уровне. Поскольку на каком-то из уровней искомая вершина обязательно находится, т. е. сумма вероятностей равна единице, то вероятность нахождения искомой вершины на i -м уровне равна отношению количества вершин i -го уровня к общему количеству вершин дерева:
Среднее количество сравнений (математическое ожидание) равно:
Первое слагаемое равно k , а для вычисления второго слагаемого можно использовать известную формулу:
Таким образом, после преобразований получаем выражение:
Так как нас интересуют достаточно грубые оценки, то при больших k мы можем считать значение дроби приблизительно равным единице. Тогда n = k-1 . Следовательно, максимальная и средняя сложность поиска информации в идеальном дереве почти совпадают.
- Сколько существует различных бинарных деревьев с n вершинами?
- Сколько среди них вырожденных и как часто они возникают?
- Сколько среди деревьев идеальных или близких к идеальным, какие последовательности значений их порождают?
Ответы на эти вопросы важны потому, что если большинство деревьев — вырожденные, то деревья почти не имеют преимуществ перед списками, а недостаток очевиден — для деревьев требуется больше памяти. Если же большинство деревьев близки к идеальным, то дерево как структура данных для хранения информации имеет большое значение и стоит приложить усилия к совершенствованию процедур работы с деревьями (например, чтобы совсем исключить появление вырожденных деревьев).
На следующем шаге мы рассмотрим число бинарных деревьев .
Источник
Дерево как структура данных
Какую выгоду можно извлечь из такой структуры данных, как дерево? В этой статье мы расскажем о данных в виде дерева, рассмотрим основные определения, которые следует знать, а также узнаем, как и зачем используется дерево в программировании. Спойлер: бинарные деревья часто применяют для поиска информации в базах данных, для сортировки данных, для проведения вычислений, для кодирования и в других случаях. Но давайте обо всем по порядку.
Основные термины
Дерево — это, по сути, один из частных случаев графа. Древовидная модель может быть весьма эффективна в случае представления динамических данных, особенно тогда, когда у разработчика стоит цель быстрого поиска информации, в тех же базах данных, к примеру. Еще древом называют структуру данных, которая представляет собой совокупность элементов, а также отношений между этими элементами, что вместе образует иерархическую древовидную структуру.
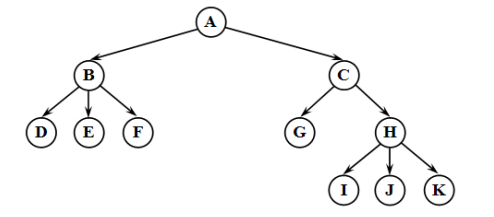
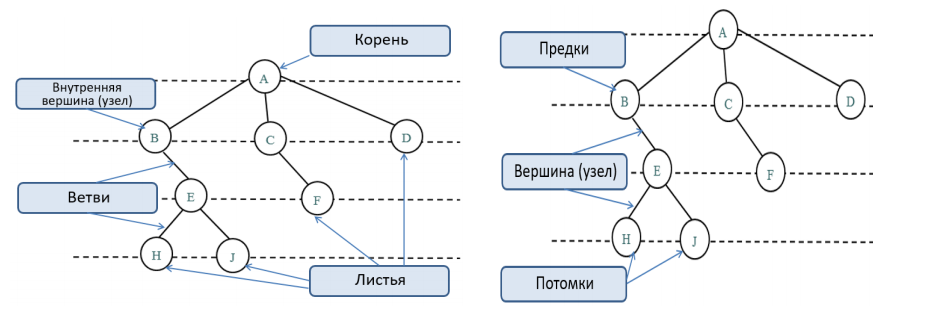
Каждый элемент — это вершина или узел дерева. Узлы, соединенные направленными дугами, называются ветвями. Начальный узел — это корень дерева (корневой узел). Листья — это узлы, в которые входит 1 ветвь, причем не выходит ни одной.
Общую терминологию можно посмотреть на левой и правой части картинки ниже:
Какие свойства есть у каждого древа:
— существует узел, в который не входит ни одна ветвь;
— в каждый узел, кроме корневого узла, входит 1 ветвь.
На практике деревья нередко применяют, изображая различные иерархии. Очень популярны, к примеру, генеалогические древа — они хорошо известны. Все узлы с ветвями, исходящими из единой общей вершины, являются потомками, а сама вершина называется предком (родительским узлом). Корневой узел не имеет предков, а листья не имеют потомков.
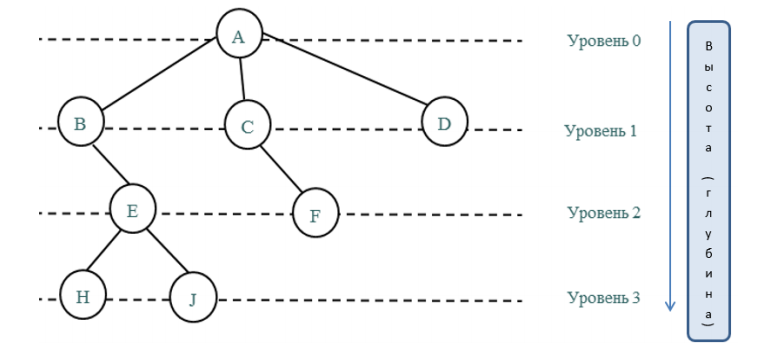
Также у дерева есть высота (глубина). Она определяется числом уровней, на которых располагаются узлы дерева. Глубина пустого древа равняется нулю, а если речь идет о дереве из одного корня, тогда единице. В данном случае на нулевом уровне может быть лишь одна вершина – корень, на 1-м – потомки корня, на 2-м – потомки потомков корня и т. д.
Ниже изображен графический вывод древа с 4-мя уровнями (дерево имеет глубину, равную четырем):
Следующий термин, который стоит рассмотреть, — это поддерево. Поддеревом называют часть древообразной структуры, которую можно представить в виде отдельного дерева.
Идем дальше. Древо может быть упорядоченным — в данном случае ветви, которые исходят из каждого узла, упорядочены по некоторому критерию.
Степень вершины в древе — это число ветвей (дуг), выходящих из этой вершины. Степень равняется максимальной степени вершины, которая входит в дерево. В этом случае листьями будут узлы, имеющие нулевую степень. По величине степени деревья бывают:
— двоичные (степень не больше двух);
— сильноветвящиеся (степень больше двух).
Деревья — это рекурсивные структуры, ведь каждое поддерево тоже является деревом. Каждый элемент такой рекурсивной структуры является или пустой структурой, или компонентом, с которым связано конечное количество поддеревьев.
Когда мы говорим о рекурсивных структурах, то действия с ними удобнее описывать посредством рекурсивных алгоритмов.
Обход древа
Чтобы выполнить конкретную операцию над всеми вершинами, надо все эти узлы просмотреть. Данную задачу называют обходом дерева. То есть обход представляет собой упорядоченную последовательность узлов, в которой каждый узел встречается лишь один раз.
В процессе обхода все узлы должны посещаться в некотором, заранее определенном порядке. Есть ряд способов обхода, вот три основные:
— прямой (префиксный, preorder);
— симметричный (инфиксный, inorder);
— обратный (постфиксный, postorder).
Существует много древовидных структур данных: двоичные (бинарные), красно-черные, В-деревья, матричные, смешанные и пр. Поговорим о бинарных.
Бинарные (двоичные) деревья
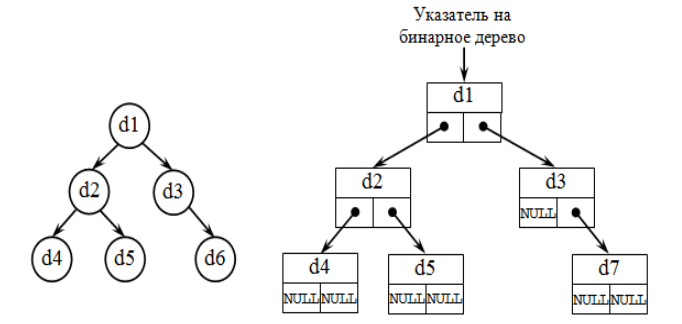
Бинарные имеют степень не более двух. То есть двоичным древом можно назвать динамическую структуру данных, где каждый узел имеет не большое 2-х потомков. В результате двоичное дерево состоит из элементов, где каждый из элементов содержит информационное поле, а также не больше 2-х ссылок на различные поддеревья. На каждый элемент древа есть только одна ссылка.
У бинарного древа каждый текущий узел — это структура, которая состоит из 4-х видов полей. Какие это поля:
— информационное (ключ вершины);
— служебное (включена вспомогательная информация, однако таких полей может быть несколько, а может и не быть вовсе);
— указатель на правое поддерево;
— указатель на левое поддерево.
Самый удобный вид бинарного древа — бинарное дерево поиска.
Что значит древо в контексте программирования?
Мы можем долго рассуждать о математическом определении древа, но это вряд ли поможет понять, какие именно выгоды можно извлечь из древовидной структуры данных. Тут важно отметить, что древо является способом организации данных в форме иерархической структуры.
В каких случаях древовидные структуры могут быть полезны при программировании:
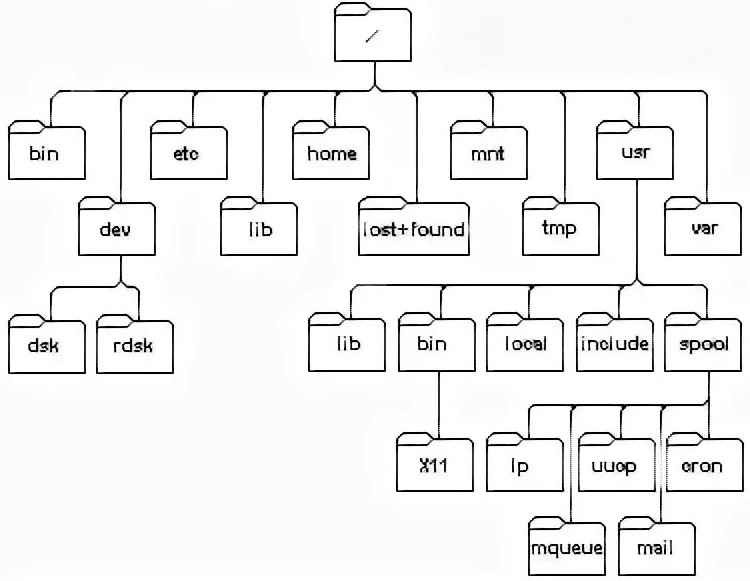
- Когда данная иерархия существует в предметной области разрабатываемой программы. К примеру, программа должна обрабатывать генеалогическое древо либо работать со структурой каталогов. В таких ситуациях иногда есть смысл сохранять между объектами программы существующие иерархические отношения. В качестве примера можно вывести древо каталогов операционной системы UNIX:
- Когда между объектами, которые обрабатывает программа, отношения иерархии не заданы явно, но их можно задать, что сделает обработку данных удобнее. Как тут не вспомнить разработку парсеров либо трансляторов, где весьма полезным может быть древо синтаксического разбора?
- А сейчас очевидная вещь: поиск объектов более эффективен, когда объекты упорядочены, будь то те же базы данных. К примеру, поиск значения в неструктурированном наборе из тысячи элементов потребует до тысячи операций, тогда как в упорядоченном наборе может хватить всего дюжины. Вывод прост: раз иерархия — эффективный способ упорядочивания объектов, почему же не использовать древовидную иерархию для ускорения поиска узлов со значениями? Так и происходит: если вспомнить бинарные деревья, то на практике их можно применять в следующих целях:
— поиск данных в базах данных (специально построенных деревьях);
— сортировка и вывод данных;
— вычисления арифметических выражений;
— кодирование по методу Хаффмана и пр.
Источник