Сортировка выворачиванием
Программист из Индии наглядно показывает Zig-Zag, Zig-Zig и Zig, используемые в алгоритме SplaySort:
В этом сезоне мы изучаем разнообразные кучи и как их можно использовать для сортировки. Однако на сей раз мы сделаем шаг в сторону от магистральной темы. Сегодняшняя структура — splay tree — кучей не является. Но оно нам нужно, чтобы морально подготовиться к изучению очередной кучи — на следующей неделе будет лекция про сортировку декартовым деревом.
Статья подготовлена при поддержке компании EDISON.
Одно из направлений нашей деятельности — автоматизация измерений и экспертные системы, благодаря чему выполняем высокотехнологичные проекты, используя строгий научный подход.
Мы очень любим computer science! 😉
Сортировка бинарным деревом поиска :: Binary search tree sort
Splay tree — это улучшенное бинарное дерево поиска. Сначала давайте вспомним как сортировать с помощью обычного «неулучшенного» двоичного дерева.
Как вы прекрасно знаете, в бинарном дереве любой левый потомок меньше чем родитель, любой правый потомок не меньше (т.е. больше или равен) чем родитель.
Сортировка в целом несложная:
- Этап 1. На основании массива строим бинарное дерево поиска. Первый элемент массива кладём в корень, остальные элементы сравниваем сначала с корнем, затем, в зависимости от сравнения, движемся вниз по левым или правым веткам (и по пути сравниваем элемент массива с имеющимися узлами дерева). В конце концов очередной элемент доходит до конца какой-либо ветки и сам становится узлом.
- Этап 2. Обходим построенное бинарное дерево поиска от минимума к максимуму. Дело в том, что строгая организация этого дерева (левый потомок меньше чем родитель, а правый больше или равен чем родитель) позволяет простым рекурсивным способом обойти данное дерево от меньших элементов к большим. Что в свою очередь выдаёт узлы дерева в возрастающем порядке.
А вот на втором этапе не всё так радужно. Рекурсивный обход дерева может запросто стать долгим путешествием по крайне извилистому лабиринту и временна́я сложность часто деградирует до .
Splay tree
Для решения этой проблемы всего каких-то 35-37 лет назад два учёных-саентиста Роберт Тарьян и Дэниел Слитор разработали эту древовидную структуру. Они предложили при любых операциях (вставка, поиск, удаление) с любым узлом дерева сразу же производить перебалансировку дерева, делая узел корнем всей структуры.
На левом фото Роберт Тарьян (первый ряд, второй справа) в компании с Архитектором Матрицы и изобретателем Паскаля. На правом фото Дэниел Слитор.
При клике по изображению откроется полноформатный вариант.
На русском языке прижилось неудачное название «расширяющееся дерево», реже — «косое дерево». Хотя если бы просто дословно перевели, то «развёрнутое дерево» (а ещё лучше — «вывернутое») и звучит неплохо и точнее отражает сущность этой алгоритмической структуры. Но то такое.
Для того чтобы вытолкнуть узел в корень, используются специальные несложные операции, так называемые повороты:
Поворот Zig
Если элемент который нужно сделать корнем находится на втором уровне вложенности, то всё чрезвычайно просто.
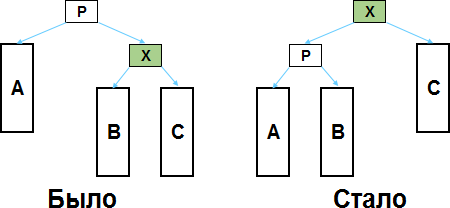
Обозначим этот элемент как X, а его родителя (являющегося также корнем дерева) — как P.
A, B, C — это поддеревья. Сколько там в этих поддеревьях узлов неважно, интересуют только корни этих поддеревьев, которые имеют отношения «родитель-потомок» с X и P. Если какие-либо из поддеревьев отсутствуют (то есть если у X и P нет каких-то потомков), то это никак не влияет на порядок действий.
Чтобы сделать X корнем дерева, нужно изменить отношение на обратное «родитель-потомок» между X и P, а также перевесить поддерево B — оно было правым потомком X, стало левым потомком P (с A и C вообще ничего делать не нужно). И это всё! В результате этих простейших манипуляций структура как была бинарным деревом поиска, так им и осталась — нигде не окажется нарушенным принцип «левый потомок меньше чем родитель, правый потомок больше или равен, чем родитель».
На предыдущей картинке X являлся левым потомком для P. Если бы X был правым потомком, то ситуацию нужно просто отзеркалить:
Если X имеет не второй уровень сложности, а третий, то всё сложнее, но ненамного.
Если X имеет родителя P, у которого в свою очередь есть родитель G, то имеем всего две разных ситуации:
1) если X является с той же стороны потомком для P, что и P для G;
2) если X и P являются разносторонними потомками для своих родителей.
Сначала рассмотрим первый случай.
Поворот ZigZig
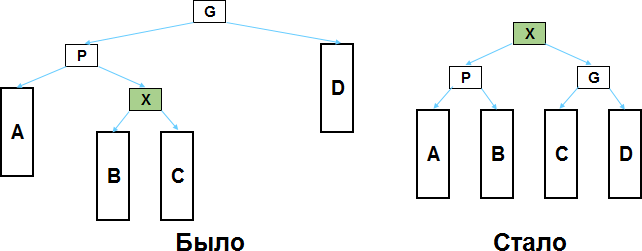
Пусть X — это левый потомок для P, а P — левый потомок для G (вариант, когда X и P являются одновременно правыми потомками решается аналогично).
Как видите, нужно изменить взаимоотношения между X, P и G, а также правильно перевесить поддеревья B и C. И наше бинарное дерево поиска от этого никак не пострадает.
Поворот ZigZag
Если X правый потомок, а P левый (или X левый, а P правый, не суть), то я надеюсь вам уже всё понятно из этой картинки:
Если X в дереве находится ещё на более низком уровне вложенности, то для его поднятия нужно применить ZigZig или ZigZag (если нужно — то сделать это несколько раз) к тому родителю вверх по ветке, который находится на третьем уровне вложенности.
Сортировка выворачиванием :: Splay sort
Собственно, здесь мы выполняем те же пункты что и в сортировке деревом — сначала выстраиваем binary sort tree, затем обходим его. Но каждый раз когда вставляем в дерево новый узел — применяя зиги и заги, делаем его корнем.
На первом этапе выигрыша это не даёт, вставка одного узла (с учётом того, что приходится зигзаговать чтобы сделать его корнем) в среднем обходится в — и таким образом сложность этого этапа .
Однако в итоге с деревом происходят удивительные трансформации — оно распрямляется и всё время поддерживается в таком распрямлённом состоянии. И это решающим образом ускоряет второй этап (обход дерева), так как получающаяся итоговая лесенка обрабатывается со сложностью O(n).
Таким образом, общая сложность алгоритма (худшая, средняя, лучшая) по времени получается .
На практике эта сортировка работает медленнее, чем MergeSort, QuickSort и прочие HeapSort, но зато наглядно демонстрирует, как можно ускорить операции с binary search tree.
Мораль сей басни такова: если приходится иметь дело с бинарным деревом поиска — если это возможно, делайте его самобалансирующим. Как возможный вариант — работайте с ним как со splay tree, т.е. при любом действии с любым узлом дерева делайте этот узел корнем. Конечно, есть и другие альтернативные самобалансирующиеся деревья поиска (красно-чёрное дерево, АВЛ-дерево и т.п.), которые, возможно, могут оказаться более предпочтительными.
Код на C
/* *------------------------------------------------------------ * * File. $RCSfile: splaysort.c,v $ * Revision. $Revision: 1.2 $ * Author. Gary Eddy (gary@cs.mu.OZ.AU) * Alistair Moffat (alistair@cs.mu.OZ.AU) * Date. $Date: 1995/09/07 06:19:17 $ * * Description: * Sorts by repeated insertion into a splay tree. * Insertions are done top down * *------------------------------------------------------------ */ #include #include #include #include char *sort_name = "Splaysort"; char *sort_version = "$Revision: 1.2 $"; /* ** Define DATAPTR for the 12 byte per record version of the program. ** Otherwise only 8 extra bytes per record are used and data ** references are done by indexing the data array. ** Different compiler/architecture combinations can cause wild ** variation in the ratio of speeds between these variations. */ #define DATAPTR #ifdef DATAPTR #define DATA(p) ((p)->data) #else #define DATA(p) (A+size*(p-T)) #endif /* ** With the fast copy option enabled a more intelligent copy is used ** depending on the size of the items being copied. ** This approach adopted from the nqsort program of Bentley and McIlroy, ** see Software Practice and Experience, v23, n11, November 1993, 1249-65. */ #define FASTCOPY #ifdef FASTCOPY #define COPYCODE(TYPE, parmi, parmj, n) < \ long i = (n) / sizeof (TYPE); \ register TYPE *pi = (TYPE *) (parmi); \ register TYPE *pj = (TYPE *) (parmj); \ do < \ *pi++ = *pj++; \ >while (--i > 0); \ > void copyfunc(char *d, char *s, int size, int copytype) < if(copytype #define COPY(d,s,size) \ if (copytype == 0) < \ *(long *)(d) = *(long *)(s); \ >else \ copyfunc(d, s, size, copytype) #else #define COPY(d,s,size) memcpy(d,s,size) #endif typedef struct node_rec node; struct node_rec < node *left, *rght; #ifdef DATAPTR char *data; #endif >; /* * sort(): * The entire sort code * * Accesses outside variables: none * * Return value. none */ void sort(void *A, size_t n, size_t size, int (*cmp)(const void *, const void *)) < register node *next, *curr, *prnt; char *item; node *l, *r, *ch; node root, *T, *new, *end, *move; #ifndef DATAPTR char *p; #endif /* ** Determine which copying method will be used. */ #ifdef FASTCOPY int copytype=((char *)A - (char *)0) % sizeof(long) || size % sizeof(long) ? 2 : size == sizeof(long) ? 0 : 1; #endif if(n < 2) return; if((T = new = (node *) malloc(sizeof(*T)*n)) == NULL) < fprintf(stderr, "Couldn't allocate space for structure\n"); >/* ** Do the first insertion manually to avoid the empty tree ** case in the main loop. */ curr = new++; item = A; curr->left = curr->rght = NULL; #ifdef DATAPTR curr->data = item; #endif item += size; end = T+n; /* ** For each item move down the tree dividing it into ** two subtrees, one containing items less than the new ** element and the other those which are greater. ** The pointers l and r refer to the greatest element in the ** smaller subtree and the smallest element in the large ** subtree respectively. During the splitting of the tree ** l and r retain children that may be incorrect in the final ** tree but these false links are cut at the end of the ** insertion. */ for( ; newleft) == NULL) < r = r->left = curr; break; > /* Left zig-zig */ else if(cmp(item, DATA(ch)) < 0) < curr->left = ch->rght; ch->rght = curr; r = r->left = ch; curr = ch->left; > /* Left zig-zag */ else < r = r->left = curr; l = l->rght = ch; curr = ch->rght; > > else < /* Right root case */ if((ch = curr->rght) == NULL) < l = l->rght = curr; break; > /* Right zig-zag */ else if (cmp(item, DATA(ch)) < 0) < l = l->rght = curr; r = r->left = ch; curr = ch->left; > /* Right zig-zig */ else < curr->rght = ch->left; ch->left = curr; l = l->rght = ch; curr = ch->rght; > > > /* Cut false links */ r->left = l->rght = NULL; new->rght = root.left; new->left = root.rght; #ifdef DATAPTR new->data = item; #endif curr = new++; item += size; > /* Now copy all of the data back into the input array. ** Uses an iterative destructive inorder traversal. ** Last item inserted is the current root. */ prnt = NULL; move = T; while (1) < if ((next = curr->left) != NULL) < /* left subtree exists */ curr->left = prnt; prnt = curr; curr = next; > else < next = curr->rght; curr->rght = move++; if (next != NULL) < /* and arrange for a visit */ if((curr = next->left) != NULL) < next->left = prnt; prnt = next; continue; > else < curr = next; continue; >> /* no right subtree either, turn around*/ if (prnt != NULL) < curr = prnt; prnt = prnt->left; curr->left = NULL; continue; > /* nothing left to be done */ break; > > #ifndef DATAPTR /* ** Change the goes-to array in rght to a comes_from in left. ** Note the kludge on pointers, where left points into the ** character array containing the elements. */ for(next = T, p = A; next < end; p += size, next++) next->rght->left = (node *)p; /* and use the `comes from' array to unscramble the permutation */ item = (char *)malloc(size); for (next=T; nextleft == NULL) continue; curr = next; final = datacurr = DATA(curr); COPY(item, datacurr, size); while ((char *)(curr->left) != final) < dataleftcurr = (char *)(curr->left); COPY(datacurr, dataleftcurr, size); prnt = curr; curr = T + (((char *)(curr->left)-A)/size); prnt->left = NULL; datacurr = dataleftcurr; > COPY(datacurr, item, size); curr->left = NULL; > #else /* Change the goes-to array in rght to a comes_from in left */ for(next = T; next < end; next++) next->rght->left = next; /* and use the `comes from' array to unscramble the permutation */ /* ** This 12 byte version uses the presence of the data pointer ** by making it the flag for already placed items. This means ** that left pointers can point to nodes, eliminating the ** calculation to find the next node. */ item = (char *)malloc(size); for (next=T; nextleft == next) continue; final = datacurr = DATA(next); curr = next->left; COPY(item, datacurr, size); while ((dataleftcurr = DATA(curr)) != final) < COPY(datacurr, dataleftcurr, size); prnt = curr; curr = curr->left; DATA(prnt) = (char *) NULL; datacurr = dataleftcurr; > COPY(datacurr, item, size); DATA(curr) = (char *) NULL; > #endif free(item); free(T); > /* sort() */Трейлер следующей серии
А мы возвращаемся к кучам. Следующая вещица будет поинтереснее той, что мы рассмотрели сегодня. Это гибрид — древовидная структура данных, являющаяся одновременно и кучей и бинарным деревом поиска.
Кликните по анимации, чтобы перейти в статью с этой сортировкой.
Ссылки
Binary search tree, Splay tree
Splay-деревья
Источник