Использование деревьев при хранении данных кратко

Хранение данных в дереве. Это как вообще?

Знакомство с Trie: это дерево, которое помогает работать со словарями.

Эта статья из области «Как бывает». Она довольно сложная, но может существенно расширить ваши горизонты в вопросах компьютеров, данных и программирования. Статья навеяна нашим разговором с Романом Халкечевым — руководителем направления аналитики в «Еде» и «Лавке». Прочитайте, там интересное о дата-сайенсе, машин-лёрнинге и карьер-билдинге.

Формальное определение

Trie (префиксное дерево, бор, или нагруженное дерево) — это структура данных, n-арное дерево, в узлах которого хранятся не ключи, а символы. А ключ — это путь от корня дерева до этого узла. Пока сложно. Теперь по порядку.

Почти всё, чем мы пользуемся в интернете, — это данные: личная информация пользователей, список товаров и покупок, картинки и текст для вёрстки, история поисковых запросов. Эти данные надо как-то хранить, чтобы в определённый момент быстро подойти и достать нужные.

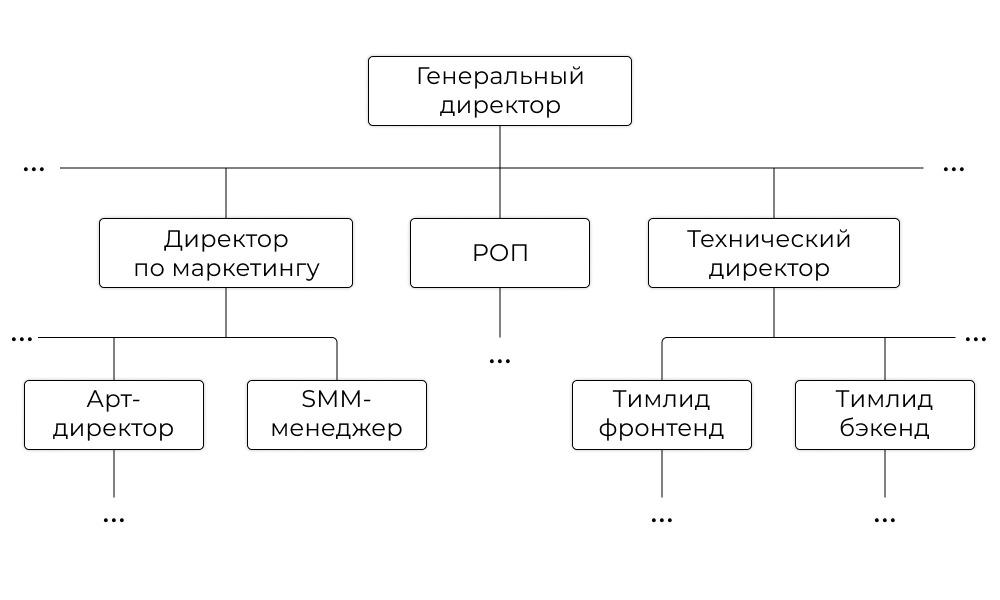
Например, часто данные хранятся в таблицах. Это не единственный способ, но довольно распространённый и интуитивно понятный. Например, у нас есть информация о структуре компании. В таблице она будет выглядеть так:

В целом понятно, но сложно представить, что кто-то будет пользоваться таким способом записи: это неудобно. Такие данные проще представить в виде дерева:

Вот мы столкнулись с понятием структуры данных.

👉 Структура данных — это то, как хранятся данные. Дерево — одна из возможных структур данных. Ещё есть связанные списки, стеки, очереди, множества, хеш-таблицы, карты и даже кучи (heap). Сейчас разберём именно деревья.

Дерево

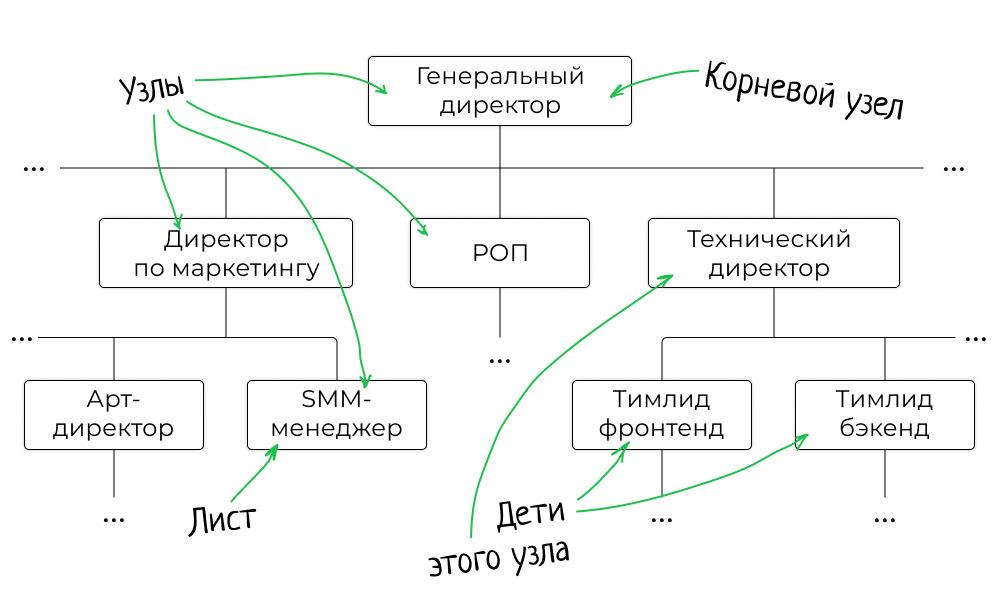
Дерево состоит из узлов и связей между ними. Самый верхний узел, из которого начинается дерево, называют корневым. Если из узла выходят другие, то их называют потомками, или детьми. Узлы второго уровня — потомки корневого узла. Если у узла нет детей, то его называют листом.

Двоичное дерево

Двоичное дерево — это тоже дерево, но у каждого узла может быть только два потомка. Чтобы распределять данные в таком дереве, используют правило: если новое значение меньше, чем значение узла, то оно становится левым ребёнком, а если больше, то правым.

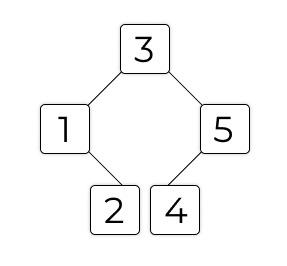
Давайте на примере: расставим числа 3, 1, 5, 2 и 4 в виде двоичного дерева. Добавлять узлы будем именно в таком порядке.

3 — корневой узел, самый верхний. Теперь нужно добавить 1. 1 < 3, значит, становится его левым потомком. Теперь 5. 5 >3, значит, становится правым потомком. Теперь 2. 2 < 3, значит, идём налево. 2 >1, значит, становится его правым потомком. Теперь 4. 4 > 3, так что идём направо. 4 < 5, так что становится его левым ребёнком. Вот так вот:

Если в дереве не цифры, а строки, то можно сравнивать их по алфавиту. Первая буква потомка по алфавиту раньше, чем у узла — ставим потомка слева. И наоборот.

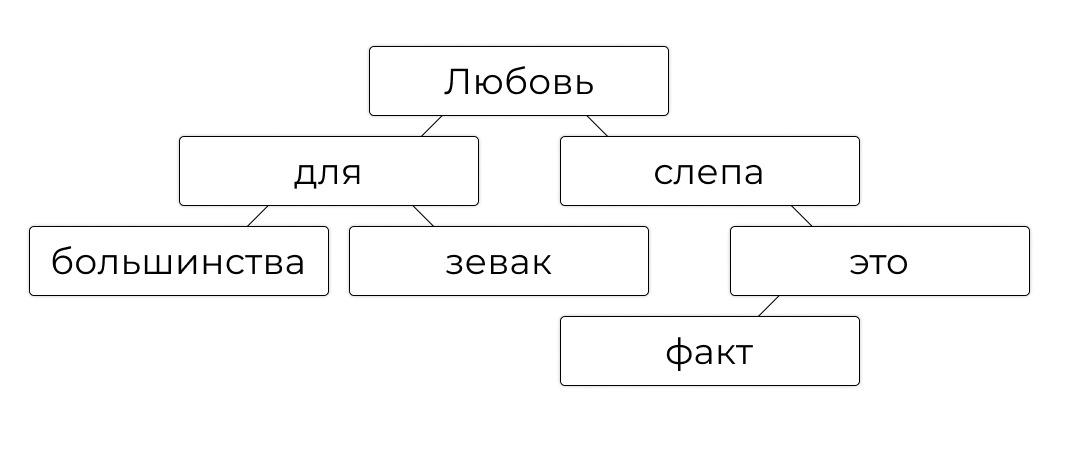
Из-за такой структуры по бинарным деревьям удобно искать: нужно сравнить запрос с текущим узлом, а потом пойти направо или налево. Например, вот бинарное дерево с цитатой из трека «Касты»:

Допустим, мы хотим найти в этом дереве слово «зевак». Получается такой путь:

Шаг 1. Смотрим на корень дерева — «Любовь». Это то, что мы ищем? Нет. Искомое значение больше или меньше? Меньше, потому что «з» в алфавите раньше, чем «л». Идём налево.

Шаг 2. Смотрим на левого потомка — «для». Это то, что мы ищем? Нет. Искомое значение больше или меньше? Больше, потому что «з» в алфавите позже, чем «д». Идём направо.

Шаг 3. Смотрим на правого потомка — «зевак». Это то, что мы ищем? Да. Отлично, мы на месте.

Вы наверняка пользовались словарями — орфографическими или толковым. Там поиск работает похожим образом: мы ищем какое-то слово и для этого сравниваем его с теми, на которые натыкаемся, пока перелистываем страницы. И потом листаем словарь вперёд или назад, если недолистали или перелистали, двигаемся вниз по двоичному дереву.

N-арное дерево

На дереве со структурой компании мы видели, что у узла может быть не только два, но и больше потомков. Такие деревья называют n-арными — у узлов в нём может быть n детей: и 1, и 5, и 200.

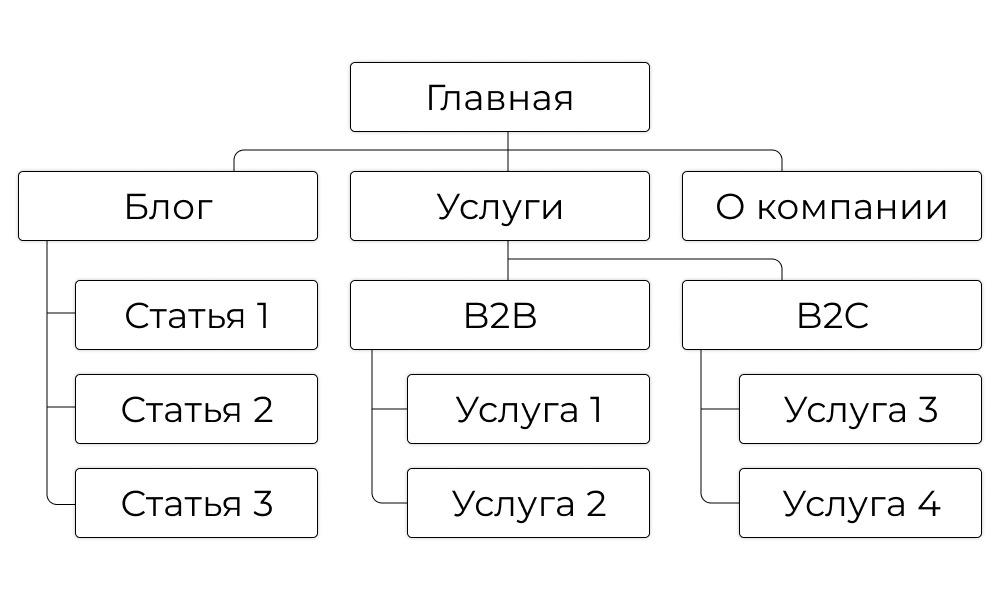
N-арное дерево может, например, изображать структуру сайта. Вот так:

Trie

Trie — это пример n-арного дерева. Но в его узлах хранятся не ключи, а символы. Что это значит?

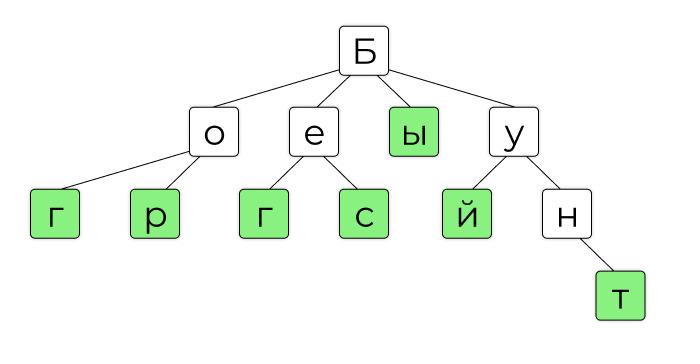
Когда мы смотрим на карту сайта, мы видим понятные значения: ссылки на «Статью 1», «О компании» или «B2B-услуги». Это и есть ключи — конкретные указатели на то, что мы ищем. В Trie в узлах таких ключей нет. Обычно там лежат строки, например буквы. Вот как может выглядеть Trie:

Ключ в Trie — это не узел, а путь от корня до определённого узла. У каждого узла есть дополнительная характеристика, которая указывает, является ли этот узел конечной точкой или промежуточным значением. На дереве выше это зелёные и белые узлы: так компьютер знает, что «Бунт» — это ключ, а «Бун» — нет.

Символов в узле может быть и несколько, например не буквы слов, а слоги. Но принцип тот же: ключ — не сам узел, а путь от корня до него.

Зачем это нужно

Trie часто используют в работе со словарями. С помощью дерева работает, например, Т9. Пользователь вводит набор цифр, а программа смотрит, какие ключи можно для такого набора получить. А потом выбирает самый популярный и подставляет его. Так из комбинации 5-6-4-2-3-6 получается «привет».

Ещё Trie помогает в подсказках в поиске. Вот что про это говорит Роман Халкечев, руководитель отдела аналитики в «Яндекс.Лавке» и «Яндекс.Еде», который несколько лет разрабатывал подсказки:

«Префиксное дерево лежит в основе быстрого поиска строк, начинающихся на префикс — символ или несколько символов, которые вводит пользователь.

В подсказках мы пользуемся модификацией этой структуры данных, которая оптимизирована по памяти и по скорости поиска. Мы заранее складываем большое количество запросов в такую структуру данных, а когда пользователь вводит префикс, мы его получаем и первым этапом ищем запросы, начинающиеся с того, что набрал пользователь. Затем уже ранжируем кандидатов и выбираем, что показать пользователю.

То есть, пользователь начинает вводить запрос, мы идём вниз по дереву и смотрим, какие запросы так начинаются. А затем сортируем их по актуальности, контексту и ещё куче параметров. И в итоге предлагаем пользователю то, что ему может быть нужно».

Источник

Обзор паттернов хранения деревьев в реляционных БД

Всем привет! Меня зовут Пантелеев Александр и я бэкенд-разработчик в компании Bimeister.

Постараюсь описать исчерпывающе, кратко и понятно суть основных паттернов хранения деревьев в реляционных базах данных. Надеюсь, что статья будет полезна тем, кто до сего момента не сталкивался с такими паттернами, и станет отправной точкой в их понимании.

В этой статье не будет терминов реляционной алгебры или базы данных: таких как атрибут, домен и т. д. Также не будет привязки к какой-либо СУБД, какому-либо SQL или пользовательскому коду.

Всего существует 4 общепринятых паттерна хранения деревьев:

Кратко рассмотрим каждый из них.

Adjacency List

Описание

Это самый простой и интуитивный вариант хранения. Каждому элементу сопоставляется его свойство — его родительский элемент. Если родительский элемент не задан, то он считается корневым элементом.
Когда связь сопоставления элемента и родительского элемента хранится отдельно от элемента, Adjacency List можно рассматривать как частный случай Closure Table со связями 1 уровня.

Преимущества

Лёгкость реализации, а также простота вставки, удаления и перемещения элементов в дереве.

Недостатки

Можно получить только непосредственные дочерние элементы. Чтобы получить все дочерние элементы, необходимо выполнить рекурсивный запрос либо производить множественные запросы.

Примеры

Родительский элемент

Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:

Nested Sets

Описание

Каждому элементу сопоставляются свойства: левый и правый индекс, на основе которых будет производиться выборка дочерних элементов. Также, но необязательно, элемент может дополняться свойством уровень для указания желаемого уровня вложенности выбираемого элемента относительно корня или родительского элемента.

Запрос получения дочерних элементов строится на том факте, что для любого дочернего элемента выполняются условия:

• левый индекс больше левого индекса родительского элемента;
• правый индекс меньше правого индекса родительского элемента.

При создании и обновлении дерева левые и правые индексы элементов дерева, при его обходе в глубину, заполняются по определённым правилам.

Преимущества

Возможность получения дочерних элементов любых уровней вложенности с помощью простого одиночного запроса.

Недостатки

При использовании целочисленных типов для левого и правого индекса и уровня необходимо пересчитывать индексы всех связанных элементов в следующих случаях:

• при вставке элементов;
• при удалении элементов;
• при изменении родительского элемента.

Пример

Левый индекс

Правый индекс

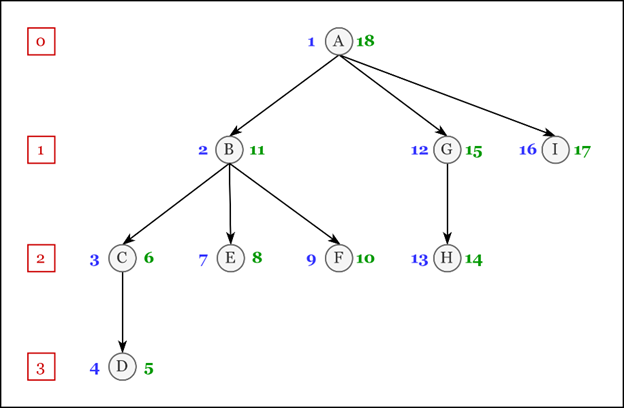
Рассмотрим элемент «B». Его значения свойств:

Чтобы получить все его дочерние элементы, нам необходимо выбрать элементы, удовлетворяющие условию:

левый индекс больше 2 И правый индекс меньше 11

Чтобы получить его непосредственные дочерние элементы, нам необходимо добавить к условию ограничение на уровень:

левый индекс больше 2 И правый индекс меньше 11 И уровень = 1

Чтобы получить дочерние элементы вместе с родительским элементом, нам необходимо ослабить условия индексов:

левый индекс больше или равен 2 И правый индекс меньше или равен 11

Closure Table

Описание

Суть этого паттерна заключается в том, что мы сопоставляем каждому элементу множество связей со всеми его дочерними элементами или сопоставляем каждому элементу множество связей со всеми его родительскими элементами. Также, но необязательно, связь может содержать свойство Уровень. Уровень задаёт расстояние между элементами в дереве.

Если в запросе получения дочерних или родительских элементов по элементу необходимо получать в результате сам элемент, то нужно добавлять связь элемента самого на себя — то есть со значением уровня связи 0.

Преимущества

Возможность получения дочерних элементов любых уровней вложенности с помощью простого одиночного запроса.

Возможность получения родительских элементов любых уровней с их иерархией относительно дочернего элемента с помощью простого одиночного запроса.

Недостатки

При вставке и удалении элементов из дерева, а также при перемещении элементов в дереве необходимо пересчитывать все связи, в которых этот элемент участвует.

Источник