Как найти корень бинарного дерева

Обход двоичного дерева на Python

Да, двоичные деревья — не самая любимая тема программистов. Это одна из тех старых концепций, о целесообразности изучения которых постоянно ведутся споры. В работе вам довольно редко придется реализовывать двоичные деревья и обходить их, так зачем же уделять им так много внимания на технических собеседованиях?

Сегодня мы не будем переворачивать двоичное дерево (ффухх!), но рассмотрим пару методов его обхода. К концу статьи вы поймете, что двоичные деревья не так страшны, как кажется.

Что такое двоичное дерево?

Недавно мы разбирали реализацию связных списков на Python. Каждый такой список состоит из некоторого количества узлов, указывающих на другие узлы. А если бы узел мог указывать не на один другой узел, а на большее их число? Вот это и есть деревья. В них каждый родительский узел может иметь несколько узлов-потомков. Если у каждого узла максимум два узла-потомка (левый и правый), такое дерево называется двоичным (бинарным).

В приведенном выше примере «корень» дерева, т. е. самый верхний узел, имеет значение 1. Его потомки — 2 и 3. Узлы 3, 4 и 5 называют «листьями»: у них нет узлов-потомков.

Строим двоичное дерево на Python

Как построить дерево на Python? Реализация будет похожей на наш класс Node в реализации связного списка. В этом случае мы назовем класс TreeNode .

Определим метод __init__() . Как всегда, он принимает self . Также мы передаем в него значение, которое будет храниться в узле.

class TreeNode: def __init__(self, value):

Установим значение узла, а затем определим левый и правый указатель (для начала поставим им значение None ).

class TreeNode: def __init__(self, value): self.value = value self.left = None self.right = None

И… все! Что, думали, что деревья куда сложнее? Если речь идет о двоичном дереве, единственное, что его отличает от связного списка, это то, что вместо next у нас тут есть left и right .

Давайте построим дерево, которое изображено на схеме в начале статьи. Верхний узел имеет значение 1. Далее мы устанавливаем левые и правые узлы, пока не получим желаемое дерево.

tree = TreeNode(1) tree.left = TreeNode(2) tree.right = TreeNode(3) tree.left.left = TreeNode(4) tree.left.right = TreeNode(5)

Обход двоичного дерева

Итак, вы построили дерево и теперь вам, вероятно, любопытно, как же его увидеть. Нет никакой команды, которая позволила бы вывести на экран дерево целиком, тем не менее мы можем обойти его, посетив каждый узел. Но в каком порядке выводить узлы?

Самые простые в реализации обходы дерева — прямой (Pre-Order), обратный (Post-Order) и центрированный (In-Order). Вы также можете услышать такие термины, как поиск в ширину и поиск в глубину, но их реализация сложнее, ее мы рассмотрим как-нибудь потом.

Итак, что из себя представляют три варианта обхода, указанные выше? Давайте еще раз посмотрим на наше дерево.

При прямом обходе мы посещаем родительские узлы до посещения узлов-потомков. В случае с нашим деревом мы будем обходить узлы в таком порядке: 1, 2, 4, 5, 3.

Обратный обход двоичного дерева — это когда вы сначала посещаете узлы-потомки, а затем — их родительские узлы. В нашем случае порядок посещения узлов при обратном обходе будет таким: 4, 5, 2, 3, 1.

При центрированном обходе мы посещаем все узлы слева направо. Центрированный обход нашего дерева — это посещение узлов 4, 2, 5, 1, 3.

Давайте напишем методы обхода для нашего двоичного дерева.

Pre-Order

Начнем с определения метода pre_order() . Наш метод принимает один аргумент — корневой узел (расположенный выше всех).

Дальше нам нужно проверить, существует ли этот узел. Вы можете возразить, что лучше бы проверить существование потомков этого узла перед их посещением. Но для этого нам пришлось бы написать два if-предложения, а так мы обойдемся одним.

def pre_order(node): if node: pass

Написать обход просто. Прямой обход — это посещение родительского узла, а затем каждого из его потомков. Мы «посетим» родительский узел, выведя его на экран, а затем «обойдем» детей, вызывая этот метод рекурсивно для каждого узла-потомка.

# Выводит родителя до всех его потомков def pre_order(node): if node: print(node.value) pre_order(node.left) pre_order(node.right)

Просто, правда? Можем протестировать этот код, совершив обход построенного ранее дерева.

Post-Order

Переходим к обратному обходу. Возможно, вы думаете, что для этого нужно написать еще один метод, но на самом деле нам нужно изменить всего одну строчку в предыдущем.

Вместо «посещения» родительского узла и последующего «обхода» детей, мы сначала «обойдем» детей, а затем «посетим» родительский узел. То есть, мы просто передвинем print на последнюю строку! Не забудьте поменять имя метода на post_order() во всех вызовах.

# Выводит потомков, а затем родителя def post_order(node): if node: post_order(node.left) post_order(node.right) print(node.value)

Каждый узел-потомок посещен до посещения его родителя.

In-Order

Наконец, напишем метод центрированного обхода. Как нам обойти левый узел, затем родительский, а затем правый? Опять же, нужно переместить предложение print!

# выводит левого потомка, затем родителя, затем правого потомка def in_order(node): if node: in_order(node.left) print(node.value) in_order(node.right)

Вот и все, мы рассмотрели три простейших способа совершить обход двоичного дерева.

Источник

Реализация бинарного дерева поиска в СИ

Бинарное дерево поиска — это набор узлов, который удовлетворяет следующим условиям:

1. Он может быть пустым.
2. Либо обладает следующими элементами: корнем, правым и левым поддеревом.
3. Ключи правого поддерева больше ключей левого поддерева.

В предыдущей статье мы рассматривали односвязные списки, которые имеют ряд достоинств, например, скорость работы. Однако бинарные деревья поиска не уступают спискам в данном показателе, напротив, найти элемент в дереве намного проще и быстрее, чем в списке. В бинарном дереве присутствует классификация элементов: одни элементы размещены в левом поддереве, а другие в правом.

Существует несколько разновидностей деревьев поиска, например, АВЛ-деревья, красно-черные и другие. В данной статье мы рассмотрим обычные бинарные деревья поиска, однако, забегая вперед стоит сказать, что разновидности обычного бинарного дерева имеют одно или несколько дополнительных параметров, которые облегчают и ускоряют работу с деревом (другие типы деревьев мы рассмотрим чуть позже в следующих статьях).

Начало начал

Бинарное дерево поиска состоит из узлов. Каждый узел содержит в себе указатели на левое и правое поддерево, указатель на родителя и ключ. Узлы представляются в качестве структуры:

• Используем typedef для создания нового типа, чтобы в дальнейшем не писать слово struct.
• int key — ключ, может быть любого типа.
• struct tree *left — указатель на левое поддерево.
• struct tree *right — указатель на правое поддерево.
• struct tree *parent — указатель на родителя.
• node — название структуры.

Инициализируем дерево

node *create(node *root, int key) < // Выделение памяти под корень дерева node *tmp = malloc(sizeof(node)); // Присваивание значения ключу tmp ->key = key; // Присваивание указателю на родителя значения NULL tmp -> parent = NULL; // Присваивание указателю на левое и правое поддерево значения NULL tmp -> left = tmp -> right = NULL; root = tmp; return root; >

Мы инициализируем дерево отдельной функцией для того, чтобы облегчить процесс добавления узлов в дерево. Другими словами, мы создаем корень бинарного дерева поиска.

Добавим узел в дерево

node *add(node *root, int key) < node *root2 = root, *root3 = NULL; // Выделение памяти под узел дерева node *tmp = malloc(sizeof(node)); // Присваивание значения ключу tmp ->key = key; /* Поиск нужной позиции для вставки (руководствуемся правилом вставки элементов, см. начало статьи, пункт 3) */ while (root2 != NULL) < root3 = root2; if (key < root2 ->key) root2 = root2 -> left; else root2 = root2 -> right; > /* Присваивание указателю на родителя значения указателя root3 (указатель root3 был найден выше) */ tmp -> parent = root3; // Присваивание указателю на левое и правое поддерево значения NULL tmp -> left = NULL; tmp -> right = NULL; /* Вставляем узел в дерево (руководствуемся правилом вставки элементов, см. начало статьи, пункт 3) */ if (key < root3 ->key) root3 -> left = tmp; else root3 -> right = tmp; return root; >

• tmp -> left и tmp -> right имеют значение NULL, так как указатель tmp расположен в конце дерева.
• Указатель root2 использовался для того, чтобы сохранить адрес на родителя вставляемого узла.
• Мы не проверяем дерево на пустоту, так как ранее дерево был инициализировано (имеется корень).

Найдем нужный узел в дереве

Поиск в дереве реализовать очень просто. Как и раньше, мы будем руководствоваться следующим правилом: слева расположены элементы с меньшим значением ключа, справа — с большим.

node *search(node * root, int key) < // Если дерево пусто или ключ корня равен искомому ключу, то возвращается указатель на корень if ((root == NULL) || (root ->key == key)) return root; // Поиск нужного узла if (key < root ->key) return search(root -> left, key); else return search(root -> right, key); >

Данная функция рекурсивная, поэтому комментарий «Если дерево пусто или ключ корня равен искомому ключу, то возвращается указатель на корень» является не совсем верным, потому что root указывает на корень только во время первой итерации, далее root ссылается на другие узлы дерева, но из-за рекурсивности функции условие if ((root == NULL) || (root -> key == key)) будет проверяться всегда.

Найдем узел с минимальным и максимальным ключом

// Минимальный элемент дерева node *min(node *root) < node *l = root; while (l ->left != NULL) l = l -> left; return l; > // Максимальный элемент дерева node *max(node *root) < node *r = root; while (r ->right != NULL) r = r -> right; return r; >

Данные функции являются очень полезными, особенно часто используются во время удаления узла из дерева.

Удалим узел из дерева

Итак, пришло время освоить, наверное, самое сложное действие с деревом, а именно, удалить узел. Удаление элемента из дерева реализуется намного сложнее, чем в списках. Это связано с особенностью построения деревьев (см. начало статьи, пункт 3).

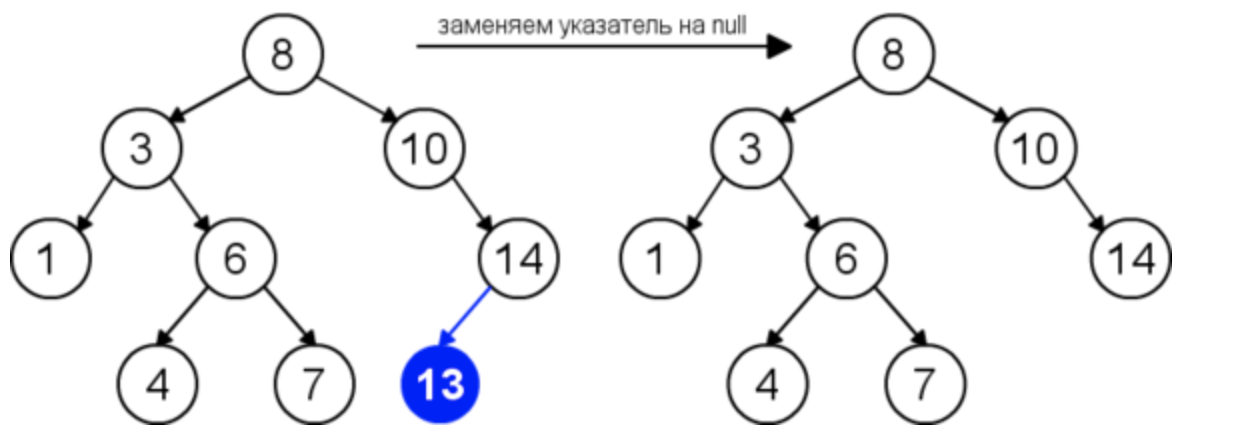
Рассмотрим самый простой случай: у удаляемого узла нет левого и правого поддерева. В данной ситуации мы просто удаляем данный лист (узел).

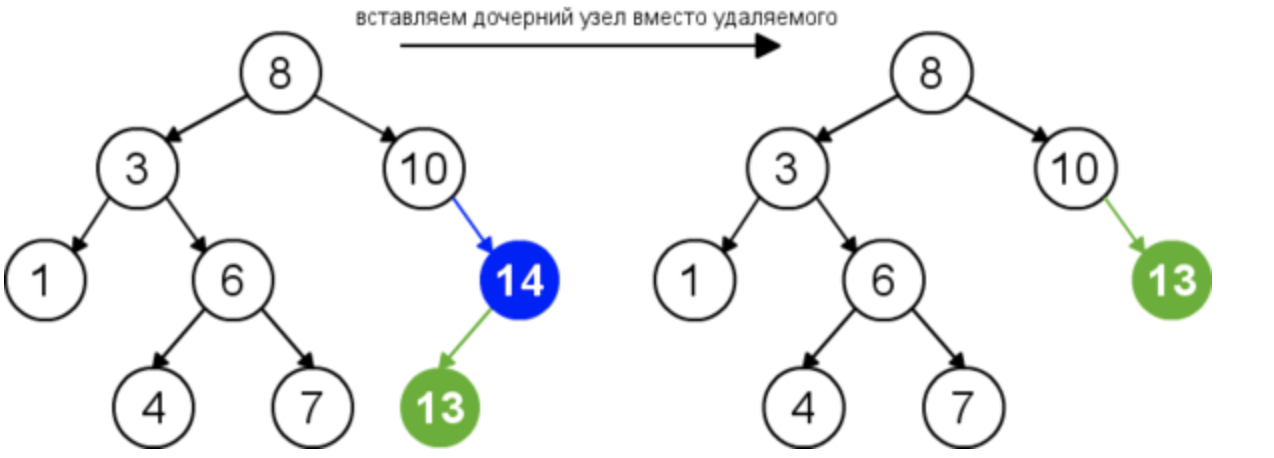
У удаляемого узла одно поддерево. В данной ситуации мы просто удаляем данный узел, а на его место ставим поддерево.

Самый сложный случай: уудаляемого узла существуют оба поддерева. В данной ситуации необходимо сначала найти следующий за удаляемым элемент, а потом его поставить на место удаляемого элемента.

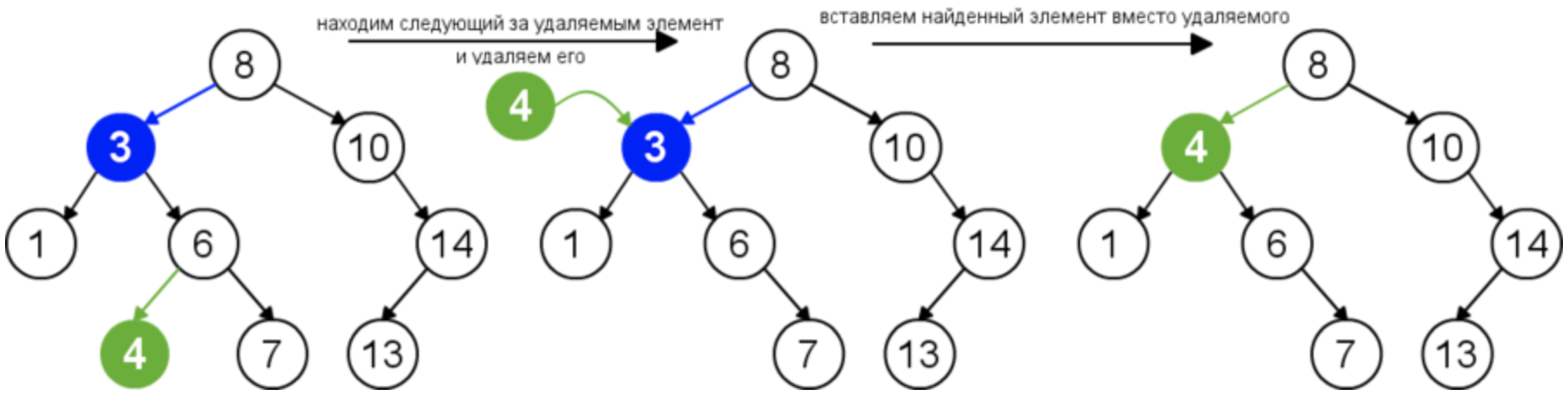
Общая функция поиска следующего за удаляемым элемента:

node *succ(node *root) < node *p = root, *l = NULL; // Если есть правое поддерево, то ищем минимальный элемент в этом поддереве if (p ->right != NULL) return min(p -> right); /* Правое дерево пусто, идем по родителям до тех пор, пока не найдем родителя, для которого наше поддерево левое */ l = p -> parent; while ((l != NULL) && (p == l -> right)) < p = l; l = l ->parent; > return l; >

В нашем случае из данного кода нужна только первая часть, так как поиск следующего за удаляемым элемента нужен тогда, когда у удаляемого узла существуют оба поддерева.

Функция удаления узла из дерева:

node *delete(node *root, int key) < // Поиск удаляемого узла по ключу node *p = root, *l = NULL, *m = NULL; l = search(root, key); // 1 случай if ((l ->left == NULL) && (l -> right == NULL)) < m = l ->parent; if (l == m -> right) m -> right = NULL; else m -> left = NULL; free(l); > // 2 случай, 1 вариант - поддерево справа if ((l -> left == NULL) && (l -> right != NULL)) < m = l ->parent; if (l == m -> right) m -> right = l -> right; else m -> left = l -> right; free(l); > // 2 случай, 2 вариант - поддерево слева if ((l -> left != NULL) && (l -> right == NULL)) < m = l ->parent; if (l == m -> right) m -> right = l -> left; else m -> left = l -> left; free(l); > // 3 случай if ((l -> left != NULL) && (l -> right != NULL)) < m = succ(l); l ->key = m -> key; if (m -> right == NULL) m -> parent -> left = NULL; else m -> parent -> left = m -> right; free(m); > return root; >

Вывод элементов дерева

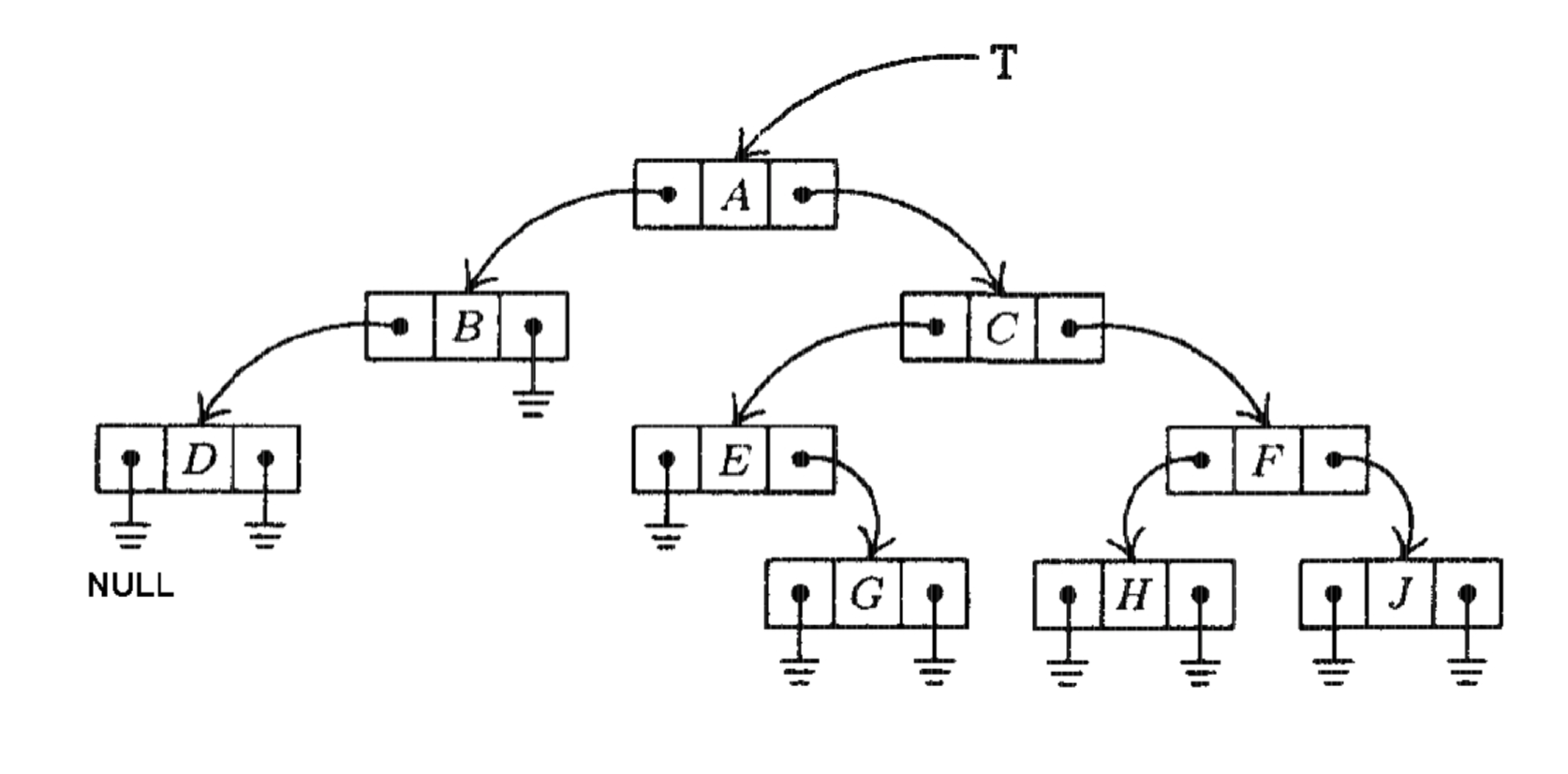
Принято выделять три типа обхода дерева:

Обход дерева в прямом порядке, будет напечатано A B D C E G F H J.

void preorder(node *root) < if (root == NULL) return; if (root ->key) printf("%d ", root -> key); preorder(root -> left); preorder(root -> right); >

void postorder(node *root) < if (root == NULL) return; postorder(root ->left); postorder(root -> right); if (root -> key) printf("%d ", root -> key); >

void inorder(node *root) < if (root == NULL) return; inorder(root ->left); if (root -> key) printf("%d ", root -> key); inorder(root -> right); >

В данной статье мы рассмотрели основные функции, которые предназначены для работы с бинарными деревьями поиска. Если у Вас остались вопросы, то просьба писать их в комментариях.

Подписывайтесь на T4S.TECH в Telegram, чтобы оставаться в курсе самых интересных новостей из мира технологий и не только.

Samsung ускоряет разработку первой в мире RAM-памяти LPDDR5 для Android-смартфонов

Samsung – это один из ведущих производителей аппаратных компонентов в отрасли, которая является для компании также основным источником дохода. Корейский производитель подтвердил свои намерения увеличить инвестиции

В App Store и Google Play в 2017 году было совершено более 175 млрд. скачиваний приложений

В прошлом году потребители потратили рекордное количество средств на приобретение мобильных приложений. Статистические данные предоставлены наблюдателями из App Annie, которая инвестировала более $86 млрд. в

Источник