АВЛ-дерево
АВЛ-дерево, или AVL tree, — древовидная структура данных с быстрым доступом к информации. Она представляет собой бинарное дерево — иерархическую схему из вершин и путей между ними, где у одной вершины может быть не более двух потомков. АВЛ-дерево – модифицированное, у него оптимизирована структура.
АВЛ-деревья придумали еще в 60-х годах советские ученые Адельсон-Вельский и Ландис. По первым буквам их фамилий и названа структура данных — АВЛ. Это модификация классического бинарного дерева поиска, благодаря которой структура лучше сбалансирована и практически не может выродиться. Вырождением называют ситуацию, когда у каждого узла оказывается только по одному потомку и структура фактически становится линейной — это неоптимально.
Освойте профессию «Аналитик данных»
Благодаря сбалансированности и борьбе с вырождением дерева информация в нем хранится более эффективно. Поэтому доступ к данным оказывается быстрее и найти их становится легче.
Кто пользуется АВЛ-деревьями
- Разработчики, которые работают с алгоритмами сортировки, хранения и поиска информации, реализуют те или иные сложные структуры. Сфера применения деревьев довольно широка, и про умение ими пользоваться могут спрашивать на собеседованиях в соответствующих отраслях.
- Аналитики данных, для которых работа с информацией — профессиональная сфера деятельности. АВЛ-деревья же — это один из методов эффективно хранить информацию и быстро получать из структуры конкретные данные. Также они могут пригодиться при реализации алгоритмов работы с данными.
- Математики, которые решают фундаментальные и практические задачи. АВЛ-деревья — подвид бинарных деревьев поиска, которые, в свою очередь, являются своеобразными графами. Все это относится к области дискретной математики: она частично пересекается с Computer Science и схожими направлениями.
Для чего нужны АВЛ-деревья
Для хранения данных. Эта структура позволяет хранить информацию в «узлах» дерева и перемещаться по ней с помощью путей, которые соединяют между собой узлы. Благодаря особому алгоритму данные хранятся относительно эффективно и с ними довольно удобно работать. Мы подробнее поговорим об этом ниже.
Находите закономерности и делайте выводы, которые помогут бизнесу
Для поисковых алгоритмов. АВЛ-деревья и бинарные деревья поиска в принципе — важная составная часть разнообразных алгоритмов поиска информации. Их применяют при построении поисковых систем и интеллектуальных сервисов.
Для сортировки. Хранение информации в АВЛ-дереве позволяет быстрее отсортировать данные, а задача сортировки часто встречается в IT. С помощью деревьев можно хранить и сортировать информацию в базах данных, в особых участках памяти, в хэшах и других структурах.
Для программных проверок. АВЛ-дерево может использоваться для решения некоторых стандартных задач, например для быстрой проверки существования элемента в структуре.
Для построения сложных структур. Дерево может быть составной частью более сложной структуры данных или какого-либо алгоритма, например используемого для поиска, хранения или принятия решений.
Для других задач. Деревья могут понадобиться везде, где нужны связные структуры данных, оптимизированные под определенные операции. Например, они могут быть более функциональной альтернативой связанному списку — линейной структуре данных, где в каждом элементе есть ссылка на предыдущий и/или следующий.
Станьте аналитиком данных и получите востребованную специальность
Как устроено двоичное дерево поиска
АВЛ-дерево — модификация двоичного, или бинарного дерева поиска. Чтобы понять, в чем его особенность, нужно сначала разобраться с бинарными деревьями в целом.
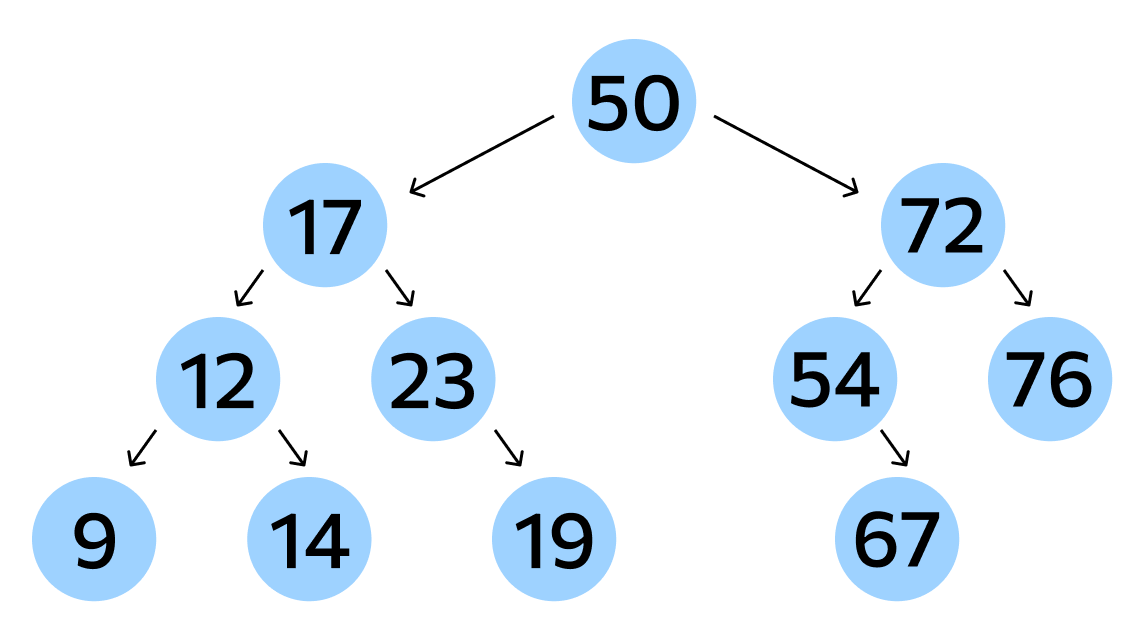
Структура. Дерево представляет собой структуру, состоящую из узлов и путей между ними, — по сути, подвид графа. Особенность в том, что дерево иерархично: у всех узлов, кроме начального, есть «родитель» и сколько-либо «потомков». Получается древовидная структура — отсюда и название.
Распределение узлов. В двоичном дереве каждый узел имеет не больше двух потомков. А двоичное дерево поиска имеет еще несколько важных характеристик. Это дерево, в котором по-особому структурированы узлы:
- все левые потомки любого узла должны иметь значения, меньшие, чем значение самого этого узла;
- все правые потомки должны быть равны или больше по значению, чем родительский узел.
Это правило должно выполняться для любого поддерева в структуре.
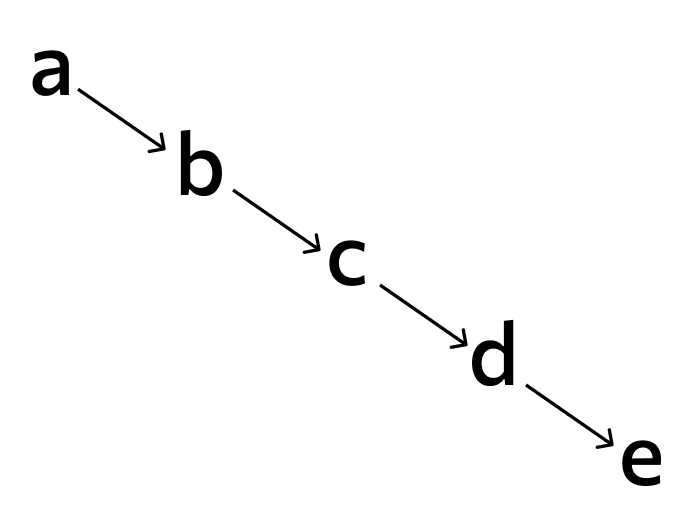
Разновидности. Дерево может быть сбалансированным, то есть с оптимально распределенной древовидной структурой, идеально сбалансированным или вырожденным: в таком случае оно фактически становится линейным, так как у каждого узла есть только один потомок. Такие деревья иногда называют лозами. Скорость выполнения операций в них становится линейной, а в сбалансированных она ближе к логарифмической, что быстрее.
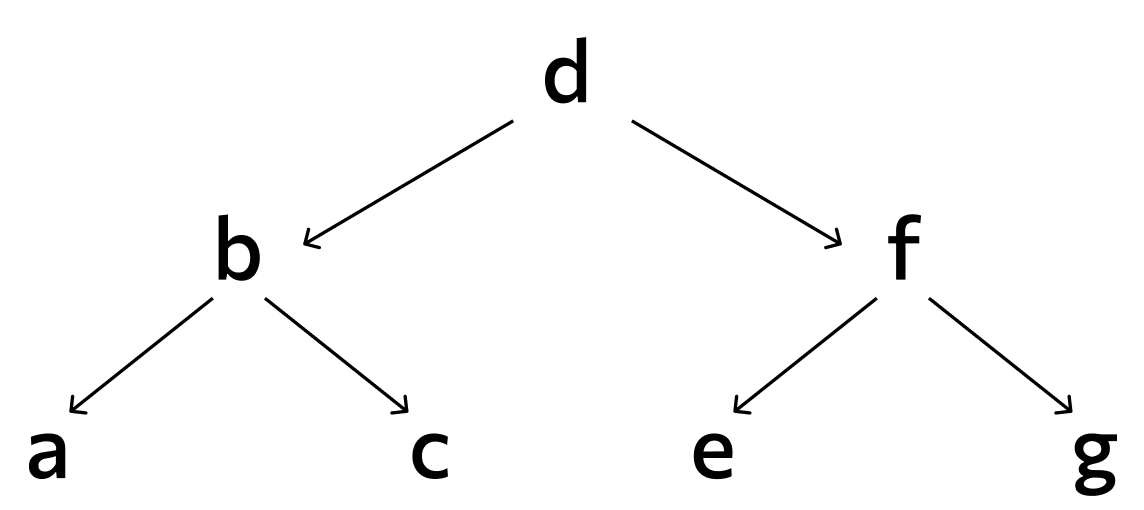
Есть и промежуточные варианты между сбалансированными и вырожденными деревьями. Чем лучше сбалансировано дерево, тем оно эффективнее. Сбалансированное дерево — такое, в котором все узлы, кроме конечных, имеют по два потомка, а все поддеревья одного уровня имеют одинаковую длину. Идеально сбалансированное дерево — как можно более широкое и низкое. Так его использование будет максимально продуктивным.
Особенности АВЛ-деревьев
АВЛ-дерево отличается от обычного бинарного дерева поиска несколькими особенностями:
- оно сбалансировано по высоте. Поддеревья, которые образованы левым и правым потомками каждого из узлов, должны различаться длиной не более чем на один уровень;
- из первой особенности вытекает еще одна — общая длина дерева и, соответственно, скорость операций с ним зависят от числа узлов логарифмически и гарантированно;
- вероятность получить сильно несбалансированное АВЛ-дерево крайне мала, а риск, что оно выродится, практически отсутствует.
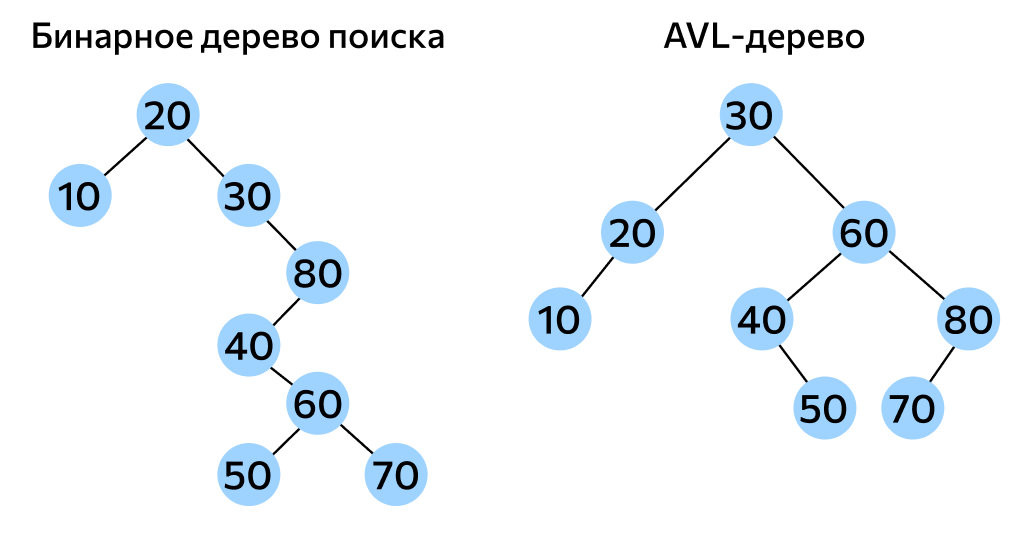
Сбалансированность такого дерева гарантирована, в отличие от так называемых рандомизированных деревьев, которые сбалансированы вероятностно — то есть с небольшой вероятностью структура все еще может выродиться.
Что такое балансировка
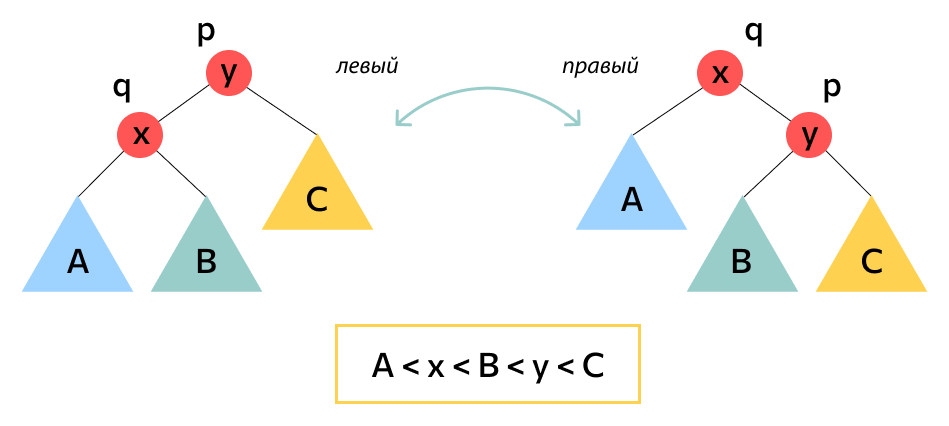
Балансировкой называют операцию, которая делает дерево более сбалансированным. В случае с АВЛ-деревьями ее применяют, если нарушается главное правило структуры: поддеревья-потомки одного узла начинают различаться больше чем на один уровень. Если разница в количестве уровней становится равна 2 или –2, запускается балансировка: связи между предками и потомками изменяются и перестраиваются так, чтобы сохранить правильную структуру.
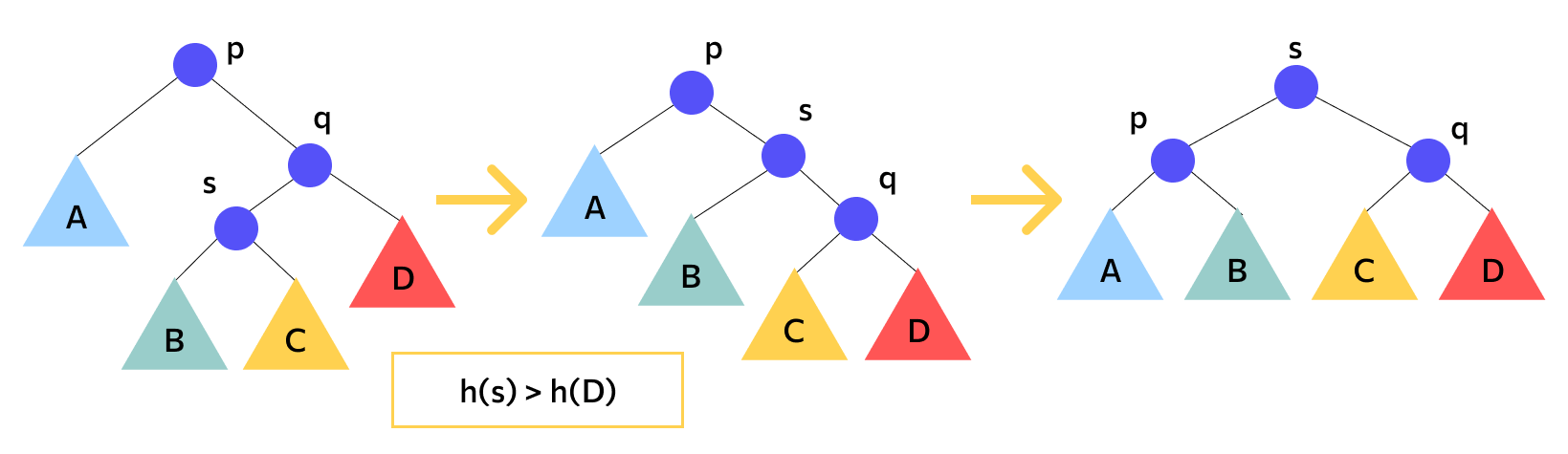
Обычно для этого какой-либо из узлов «поворачивается» влево или вправо, то есть меняет свое расположение. Поворот может быть простым, когда расположение изменяет только один узел, или большим: при нем два узла разворачиваются в разные стороны. Большой поворот эффективен там, где не сработает обычный.
Станьте аналитиком данных и получите востребованную специальность
Вставка узлов в дерево
Если в структуру данных нужно добавить новую информацию, это нужно сделать по определенному алгоритму. Он такой во всех бинарных деревьях поиска, но в случае с АВЛ-деревом алгоритм несколько дополняется: за вставкой следует обязательная балансировка.
Вставка. Чтобы вставить узел в дерево, нужно пройти от его начала вниз, на каждом шаге сравнивая значение нового узла с текущими. Алгоритм доходит до конца какого-либо поддерева и делает новый узел правым или левым его потомком в зависимости от значения. Так сохраняется главное правило двоичного дерева поиска — требование к расположению элементов по значению.
Балансировка. Особенность АВЛ-деревьев тут в том, что после вставки надо проверить соотношение длин поддеревьев и, если нужно, провести балансировку. Причем балансировку может понадобиться проводить для нескольких уровней дерева — это нормально. Алгоритм для балансирования может спускаться вниз из начального узла или подниматься вверх от свежедобавленного, по ходу движения пересчитывать разницу высот и совершать повороты, если где-то обнаружилась разница в два уровня. Балансировка продолжается, пока все значения высот не пересчитаются, а дисбаланс не будет устранен.
Удаление узлов из дерева
Удалить узел также можно по стандартным правилам, принятым для бинарного дерева поиска, но опять же с несколькими нюансами.
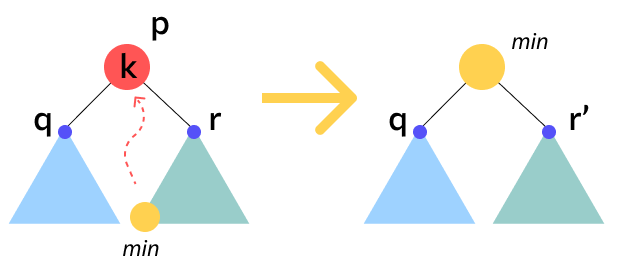
Сначала в дереве ищется узел, который нужно удалить. Если такого узла нет, ничего не делается, а вот если он находится, все куда интереснее. Надо пройти по правому поддереву удаляемого узла и найти в нем узел с самым маленьким значением — назовем его min. После этого удаляемый узел нужно заменить на узел min, и структура дерева перестроится.
Если правого поддерева у удаляемого узла нет, вместо min на место узла подставляется его левый потомок. Если левого потомка тоже нет, значит, удаляемый узел — лист, то есть потомки у него отсутствуют в принципе. Тогда его можно просто удалить и ничего не подставлять на его место.
После удаления опять же нужно пересчитать новые значения высот и провести балансировку, чтобы избежать слишком большой разницы между ветвями.
Как реализовать АВЛ-дерево
Реализация деревьев обычно сложнее, чем умозрительная структура. Но возможности для создания AVL trees есть практически в любых современных языках программирования: Java, C/C++, Python и других.
Сначала разработчик описывает структуру одного узла. Это может быть сущность, способная содержать в себе несколько переменных: в C++ для этого есть тип данных struct (структура), в Python для узла обычно создают свой класс, и так далее.
Программно описанный узел содержит в себе:
- какие-то данные, от значения которых, как говорилось выше, зависит расположение элемента — слева или справа от родителя;
- ссылки на левого и правого потомка;
- высота поддерева, которое начинается в этом узле, или разница высот между левым и правым поддеревьями.
Затем прописываются отдельные функции для определения высоты, разницы между поддеревьями и т.д.
Как сбалансировать АВЛ-дерево
Балансировка, добавление и удаление элементов — функции, которые прописываются отдельно. Обычно сначала разработчик реализует код, который совершает обычный поворот, а потом эта функция используется в другой, более крупной, отвечающей за балансировку.
Код функции балансировки сводится к проверке условий и выполнению поворотов, если проверка обнаружила дисбаланс. Сначала выполняется один простой поворот, потом, если это не помогло, — второй для другого потомка и в противоположную сторону. Так реализуется большой поворот.
Программная реализация поворота сводится к перестановке ссылок, соединяющих между собой элементы дерева. После этого пересчитываются числовые значения, которые показывают разницу между высотами.
Реализация вставки и удаления
Вставка. Функция, вставляющая элемент, обычно рекурсивная, то есть вызывает сама себя. Ее можно реализовать довольно изящно:
- вызываем функцию в начальном узле;
- если значение, которое надо вставить, меньше значения узла, где мы находимся, идем налево — вызываем ту же функцию для левого потомка;
- если значение равно или больше тому, где мы сейчас, идем направо — вызываем функцию для правого потомка;
- если мы попали в точку, где еще нет узла, создаем там узел и помещаем туда новое значение;
- вызываем функцию балансировки. Так как вставка рекурсивная, балансировка выполнится начиная с последнего открытого экземпляра функции вставки и заканчивая первым.
Удаление. Функция удаления также рекурсивная, но она сложнее. Сначала надо найти удаляемый элемент, затем перейти в его правого потомка, если он есть, и найти там минимальный узел. А потом начинаются нюансы:
- по логике структуры бинарного дерева поиска у минимального узла может быть максимум один потомок — справа. Поэтому функция, «удаляющая» минимальный узел, возвращает его правого потомка — он пригодится при замене;
- минимальный узел не удаляется безвозвратно, а подставляется на место удаляемого — опять же происходит замена ссылок;
- слева к минимальному узлу присоединяется левый потомок удаляемого узла, справа — то, что осталось от правого потомка после вычленения минимального;
- происходит балансировка.
Операции могут выглядеть сложными, особенно в части реализации. Но если вы разберетесь с тем, как работает логика деревьев, все станет понятнее. Чтобы узнать больше, можете воспользоваться нашим глоссарием или туториалами. А можете записаться на курсы и получить актуальные знания от профессионалов.
Аналитики влияют на рост бизнеса. Они выясняют, какой товар и в какое время больше покупают. Считают юнит-экономику. Оценивают окупаемость рекламной кампании. Поэтому компании ищут и переманивают таких специалистов.
Источник