Какая глубина бинарного дерева

Бинарное дерево. Основные определения и понятия. Бинарный поиск по дереву. Формирование бинарного дерева этим методом

Бинарное (двоичное) дерево (binary tree) – древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей). Бинарное дерево [др. источник] – это упорядоченное дерево, каждая вершина которого имеет не более двух поддеревьев, причем для каждого узла выполняется правило: в левом поддереве содержатся только ключи, имеющие значения, меньшие, чем значение данного узла, а в правом поддереве содержатся только ключи, имеющие значения, большие, чем значение данного узла. Бинарное дерево является рекурсивной структурой, поскольку каждое его поддерево само является бинарным деревом и, следовательно, каждый его узел в свою очередь является корнем дерева. Узел дерева, не имеющий потомков, называется листом. То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). Очевидным, но важным для понимания фактом является то, что каждое поддерево в свою очередь тоже является деревом. К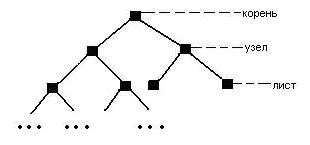аждый узел в дереве задаёт поддерево, корнем которого он является. У вершины n=(data, left, right) есть два ребёнка (левый и правый) left и right и, соответственно, два поддерева (левое и правое) с корнями left и right. Свойство. Строго бинарное дерево с n листами всегда содержит 2n-1 узлов. Уровень узла в бинарном дереве: уровень корня всегда равен нулю, а далее номера уровней при движении по дереву от корня увеличиваются на 1 по отношению к своему непосредственному предку. Глубина бинарного дерева — это максимальный уровень листа дерева, что равно длине самого длинного пути от корня к листу дерева. Полное бинарное дерево уровня n — это дерево, в котором каждый узел уровня n является листом, и каждый узел уровня меньше n имеет непустые левое и правое поддеревья Почти полное бинарное дерево — это бинарное дерево, для которого существует неотрицательное целое k такое, что: 1) Каждый лист в дереве имеет уровень k или k+1. 2) Если узел дерева имеет правого потомка уровня k+1, тогда все его левые потомки, являющиеся листами, также имеют уровень k+1. Упорядоченные бинарные деревья — это деревья, в которых для каждого узла Х выполняется правило: в левом поддереве — ключи, меньшие Х, в правом поддереве — большие или равные Х. Построение бинарного дерева. Двоичное дерево поиска. Правило построения двоичного дерева поиска: элементы, у которых значение некоторого признака меньше, чем у корня, всегда включаются слева от некоторого поддерева, а элементы со значениями, большими, чем у корня — справа. Этот принцип используется и при формировании двоичного дерева, и при поиске в нем элементов. Обратить внимание: поиск места подключения очередного элемента всегда начинается с корня. Пример: 20, 10, 35, 15, 17, 27, 24, 8, 30. Поиск элемента в бинарном дереве. При поиске элемента с некоторым значением признака происходит спуск по дереву, начиная от корня, причем выбор ветви следующего шага — направо или налево согласно значению искомого признака — происходит в каждом очередном узле на этом пути. При поиске элемента результатом будет либо найденный узел с заданным значением признака, либо поиск закончится листом с «нулевой» ссылкой, а требуемый элемент отсутствует на проделанном по дереву пути. Если поиск был проделан для включения очередного узла в дерево, то в результате будет найден узел с пустой ссылкой (пустыми ссылками), к которому справа или слева в соответствии со значением признака и будет присоединен новый узел. Двоичное дерево поиска можно определить так:

• Двоичное дерево состоит из узлов (вершин) — записей вида (data, left, right), где data — некоторые данные привязанные к узлу, left и right — ссылки на потомков.
• Данные (data) обладают ключом (key) на котором определена операция сравнения «меньше«. В конкретных реализациях это может быть пара (key, value).
• Для любого узла X выполняются свойства дерева поиска:

key[left[X]] < key[X] ≤ key[right[X]], т. е. ключи данных родительского узла больше ключей данных левого сына и нестрого меньше ключей данных правого. Основные операции в двоичном дереве поиска: FIND(K) — поиск узла, в котором хранится пара (key, value) с key = K. INSERT(K,V) — добавление в дерево пары (key, value) = (K, V). REMOVE(K) — удаление узла, в котором хранится пара (key, value) с key = K.

Для продолжения скачивания необходимо пройти капчу:

Источник

Высота и глубина бинарного дерева

Эта статья направлена ​​на то, чтобы провести различие между двумя свойствами бинарных деревьев, называемыми высотой и глубиной. В соответствии с терминологией бинарного дерева ниже приведены определения высоты и глубины бинарного дерева.

Высота. Высота бинарного дерева — это количество ребер на самом длинном пути от корневого узла до самого дальнего конечного узла.

Глубина. Глубина бинарного дерева — это количество узлов на самом длинном пути от корневого узла до самого дальнего конечного узла.

Несколько терминов бинарного дерева

Пустое дерево имеет высоту -1

Дерево только с одним узлом (корневым узлом) имеет высоту 0.

Давайте рассмотрим несколько примеров бинарного дерева, чтобы прояснить разницу.

Давайте посчитаем высоту Дерева 1, Дерева 2, Дерева 3 и Дерева 4

Дерево 1: мы отслеживаем узлы 50–70–60–55, что дает 3 ребра между узлами, следовательно, высота равна 3

Дерево 2: мы отслеживаем узлы 15–20–25, что дает 2 ребра между узлами, следовательно, высота равна 2

Дерево 3: мы отслеживаем узлы 14–15–18–21–25–45, что дает 5 ребер между узлами, следовательно, высота равна 5

Дерево 4: мы отслеживаем узлы 12–14–18–16, что дает 3 ребра между узлами, следовательно, высота равна 3

Давайте посчитаем глубину дерева 1, дерева 2, дерева 3 и дерева 4

Дерево 1: мы считаем узлы 50–70–60–55, что дает 4 узла, следовательно, глубина равна 4.

Дерево 2: мы отслеживаем узлы 15–20–25, что дает 3 узла, следовательно, глубина равна 3

Дерево 3: мы отслеживаем узлы 14–15–18–21–25–45, что дает 6 узлов, следовательно, глубина равна 6

Дерево 4: мы отслеживаем узлы 12–14–18–16, что дает 4 узла, следовательно, глубина равна 4

Давайте посмотрим на приведенный ниже фрагмент кода для определения высоты и глубины двоичного дерева.

Предположим, мы построили деревья от 1 до 4.

public class HeightDepthBST < Node root; int height (Node node) < if (node == null) return 0; else if (node.left == null && node.right == null) return 0; return 1 + Math.max (height(node.left), height(node.right)); > int depth (Node node) < if (node == null) return 0; int left = depth (node.left); int right = depth (node.right); return (left > right) ? left+1 : right+1; > public static void main(String[] args) < HeightDepthBST a = new HeightDepthBST(); a.root = a.createBST(); System.out.println("Height "+height(a.root)); System.out.println("Depth "+depth(a.root)); > Node createBST() < // Tree 4 in above root = null; root = add (root, 12); root = add (root, 6); root = add (root, 5); root = add (root, 8); root = add (root, 7); root = add (root, 9); root = add (root, 14); root = add (root, 18); root = add (root, 16); return root; > Node add (Node node, int data) < if (null == node) return new Node (data); else if (data < node.data) node.left = add (node.left, data); else if (data > node.data) node.right = add (node.right, data); return node; > > class Node < int data; Node left, right; Node (int data) < this.data=data; > >

Временная сложность кода height() и depth() составляет O(N).

Вывод

В этой статье мы проследили 2 важных свойства бинарного дерева, а именно высоту и глубину. Мы посетили код, чтобы вычислить их. Мы также увидели, в чем разница между ними с точки зрения дерева.

Источник

Деревья поиска

Дерево — одна из наиболее распространенных структур данных в программировании.

Деревья состоят из набора вершин (узлов, нод) и ориентированных рёбер (ссылок) между ними. Вершины связаны таким образом, что от какой-то одной вершины, называемой корневой (вершина 8 на рисунке), можно дойти до всех остальных единственным способом.

• Родитель вершины $v$ — вершина, из которой есть прямая ссылка в $v$.
• Дети (дочерние элементы, сын, дочь) вершины $v$ — вершины, в которые из $v$ есть прямая ссылка.
• Предки — родители родителей, их родители, и так далее.
• Потомки — дети детей, их дети, и так далее.
• Лист (терминальная вершина) — вершина, не имеющая детей.
• Поддерево — вершина дерева вместе со всеми её потомками.
• Степень вершины — количество её детей.
• Глубина вершины — расстояние от корня до неё.
• Высота дерева — максимальная из глубин всех вершин.

Деревья чаще всего представляются в памяти как динамически создаваемые структуры с явными указателями на своих детей, либо как элементы массива связанные отношениями, неявно определёнными их позициями в массиве.

Деревья также используются в контексте графов.

Бинарные деревья поиска

Бинарное дерево поиска (англ. binary search tree, BST) — дерево, для которого выполняются следующие свойства:

• У каждой вершины не более двух детей.
• Все вершины обладают ключами, на которых определена операция сравнения (например, целые числа или строки).
• У всех вершин левого поддерева вершины $v$ ключи не больше, чем ключ $v$.
• У всех вершин правого поддерева вершины $v$ ключи больше, чем ключ $v$.
• Оба поддерева — левое и правое — являются двоичными деревьями поиска.

Более общим понятием являются обычные (не бинарные) деревья поиска — в них количество детей может быть больше двух, и при этом в «более левых» поддеревьях ключи должны быть меньше, чем «более правых». Пока что мы сконцентрируемся только на двоичных, потому что они проще.

Чаще всего бинарные деревья поиска хранят в виде структур — по одной на каждую вершину — в которых записаны ссылки (возможно, пустые) на правого и левого сына, ключ и, возможно, какие-то дополнительные данные.

Как можно понять по названию, основное преимущество бинарных деревьев поиска в том, что в них можно легко производить поиск элементов:

Эта функция — как и многие другие основные, например, вставка или удаление элементов — работает в худшем случае за высоту дерева. Высота бинарного дерева в худшем случае может быть $O(n)$ («бамбук»), поэтому в эффективных реализациях поддерживаются некоторые инварианты, гарантирующую среднюю глубину вершины $O(\log n)$ и соответствующую стоимость основных операций. Такие деревья называются сбалансированными.

Источник