Бинарные деревья
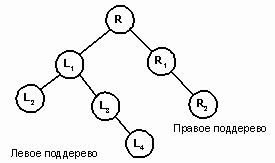
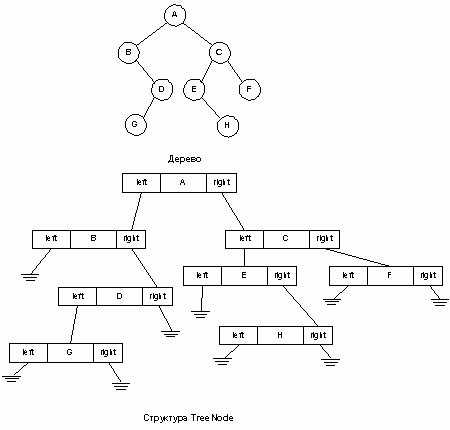
Хотя деревья общего вида достаточно важны, мы сосредоточимся на ограниченном классе деревьев, где каждый родитель имеет не более двух сыновей (рис. 4). Такие бинарные деревья (binary trees) имеют унифицированную структуру, допускающую разнообразные алгоритмы прохождения и эффективный доступ к элементам. Изучение бинарных деревьев дает возможность решать наиболее общие задачи, связанные с деревьями, поскольку любое дерево общего вида можно представить эквивалентным ему бинарным деревом.
У каждого узла бинарного дерева может быть 0, 1 или 2 сына. По отношению к узлу слева будем употреблять термин левый сын (left child), а по отношению к узлу справа – правый сын (right child). Наименования «левый» и «правый» относятся к графическому представлению дерева. Бинарное дерево является рекурсивной структурой. Каждый узел – это корень своего собственного поддерева. У него есть сыновья, которые сами являются корнями деревьев, называемых левым и правым поддеревьями соответственно. Таким образом, процедуры обработки деревьев рекурсивны.
Дадим рекурсивное определение бинарного дерева.
Бинарное дерево — это такое множество узлов B, что
а) B является деревом, если множество узлов пусто (пустое дерево – тоже дерево);
б) B разбивается на три непересекающихся подмножества:
Рис.4. Пример бинарного дерева
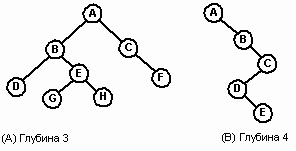
На любом уровне n бинарное дерево может содержать от 1 до 2n узлов. Число узлов, приходящееся на уровень, является показателем плотности дерева. Интуитивно плотность есть мера величины дерева (число узлов) по отношению к глубине дерева. На рис. 4 дерево А содержит 8 узлов при глубине 3, в то время как дерево B содержит 5 узлов при глубине 4. Последний случай является особой формой, называемой вырожденным (degenerate) деревом, у которого есть единственный лист (E) и каждый нелистовой узел имеет только одного сына. Вырожденное дерево эквивалентно связанному списку.
Рис.5. Бинарные деревья различной плотности
Деревья с большой плотностью очень важны в качестве структур данных, так как позволяют хранить большие коллекции данных и осуществлять эффективный доступ к элементам. Быстрый поиск – главное, что обусловливает использование деревьев для хранения данных.
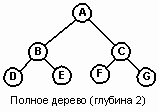
Вырожденные деревья имеют наименьшую плотность (1). Другая крайность – законченные бинарные деревья (complete binary tree) глубины N, где каждый уровень 0, 1, . N-1 имеет полный набор узлов, и все листья уровня N расположены слева. Законченное бинарное дерево, содержащее 2N узлов на уровне N, является полным. На Рис. 6 показаны законченное и полное бинарные деревья.
Законченные и полные бинарные деревья дают интересные математические факты. На нулевом уровне имеется 2 0 узлов, на первом — 2 1 , на втором — 2 2 и т.д. На первых k-1 уровнях имеется 2 k-1 узлов.
1 + 2 + 4 + . + 2 k-1 = 2 k -1
На уровне k количество дополнительных узлов колеблется от 1 до 2k (полное). В полном дереве число узлов равно
1 + 2 + 4 + . + 2 k-1 + 2 k = 2 k-1 — 1
Число узлов законченного бинарного дерева удовлетворяет неравенству
2 k N 2 k-1 — 1 2 k-1
Решая его относительно k, имеем
k log2 (N) k+1
Например, полное дерево глубины 3 имеет
2 4 — 1 = 15 узлов
Рис.6. Классификация бинарных деревьев
Структура бинарного дерева
Структура бинарного дерева состоит из узлов (рис.7). Как и в связанном списке, эти узлы содержат поля данных и указатели на другие узлы в коллекции. В этом разделе мы определим узлы дерева и операции для его построения и прохождения. Объявим класс TreeNode, реализующий функциональность узла дерева, и разработаем ряд функций, позволяющих создавать бинарные деревья и осуществлять прохождение по их узлам.
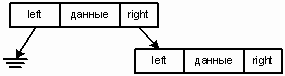
Узел дерева содержит поле данных и два поля с указателями. Поля указателей называются левым указателем (left) и правым указателем (right), поскольку они указывают на левое и правое поддерево, соответственно. Значение NULL является признаком пустого дерева.
Рис.7. Структура узлов дерева
Корневой узел определяет входную точку дерева, а поля указателей – узлы следующего уровня. Листовой узел содержит NULL в полях правого и левого указателей. Пример представления структуры дерева дан на рис. 8.
Рис.8. Представление структуры дерева
Источник
Бинарное дерево — что это? B-деревья
Статья расскажет о том, что такое бинарные деревья. Будут представлены способы их представления и основные термины. Отдельное внимание будет уделено B-дереву и его отличию от двоичных структур.
Деревом называют структуру данных, которая имеет древовидный вид, то есть характеризуется наличием набора связанных узлов. Бинарное дерево — это конечное множество элементов, связанных с двумя разными бинарными деревьями — правым и левым поддеревьями.
На что следует обратить внимание: — А — корень дерева; — B — корень левого поддерева и предок D; — С — корень правого поддерева; — D — потомок родительского узла B; если D располагается на уровне i, то B – на уровне i-1.
Необходимо выделить следующие термины: — узел (вершина) — это каждый элемент бинарного дерева; — ветви — связи между узлами; — глубина (высота) — наибольший уровень какого-нибудь элемента; — лист (терминальный узел) — термин применяется, если элемент не имеет потомков; — внутренние узлы — узлы ветвления; — степень внутреннего узла — число его потомков (наибольшая степень всех существующих узлов — это степень всего бинарного дерева); — длина пути к x — количество ветвей, которые необходимо пройти от корня до текущего узла x. Длина пути самого корня равна нулю, а узел на уровне i обладает длиной пути, которая равна i.
Использование
На практике бинарные деревья применяются, когда в каждой точке какого-нибудь вычислительного процесса нужно принимать одно из 2-х возможных решений. Существует множество задач, решаемых таким способом. Одна из них — выполнение операции, условно говоря, X с каждым элементом дерева. X рассматривается в качестве параметра обобщенной задачи посещения всех вершин либо задачи обхода дерева. Если рассмотреть такую задачу в качестве единого последовательного процесса, то можно сказать, что отдельные вершины посещаются в определенном порядке, то есть могут считаться линейно расположенными.
Способы обхода
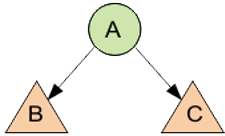
Предположим, что имеется дерево (не пустое), в котором A является корнем, а B и C — левым и правым поддеревьями.
Есть 3 способа обхода: 1. Обход в прямом порядке — сверху вниз: A, B, C — префиксная форма. 2. Обход слева направо (симметричный порядок): B, A, C — инфиксная форма. 3. Обход снизу вверх (обратный порядок): B, C, A — постфиксная форма.
Реализация
На практике вершину древа можно описать в качестве структуры:
Тогда обход в префиксной форме будет выглядеть следующим образом:
Бинарное дерево поиска
Оно представляет собой двоичное (бинарное) дерево, для которого справедлив ряд дополнительных условий. Эти условия называют свойствами:
Данные в каждой вершине должны обладать ключами, где определена операция сравнения “
Обычно информация, которая представляет каждую вершину, — это запись, а не единственное поле данных.
Чтобы составить бинарное дерево поиска, пригодится функция добавления узла:
Удаляем поддерево
B-дерево. Поиск по B-дереву
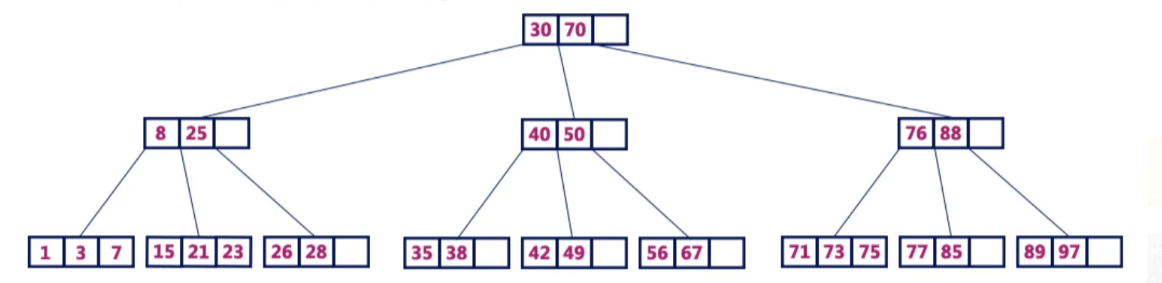
В бинарном дереве поиска каждый узел содержит лишь одно значение (ключ) и не более 2-х потомков. Но существует особый вид древа поиска, называемый B-дерево (Би-дерево). Здесь узел содержит больше одного значения и больше 2-х потомков. Также его называют сбалансированным по высоте деревом поиска порядка m (Height Balanced m-way Search Tree).
B-дерево представляет собой сбалансированное дерево поиска, где каждый узел содержит много ключей и имеет больше 2-х потомков.
Возможные операции: 1. Поиск. 2. Вставка (вставляем новый элемент). 3. Удаление.
Каждое B-дерево имеет порядок. Для примера рассмотрим B-дерево порядка m. Оно будет обладать рядом следующих характеристик:
Ниже можно посмотреть на B-дерево четвертого порядка, содержащее максимум три значения ключа и максимум четыре потомка для каждой вершины.
Поиск аналогичен поиску по двоичному дереву. Следует вспомнить, что в двоичном древе поиск начинается с корня, причем каждый раз принимается 2-стороннее решение (пойти по правому поддереву либо по левому). В В-дереве поиск тоже начинается с корневого узла, но с той лишь разницей, что на каждом шаге принимается не 2-стороннее, а n-стороннее решение, причем n для дерева в данном случае представляет общее число потомков рассматриваемого узла. Сложность поиска такого дерева — O(log n).
Также существует такое понятие, как вставка в B-дерево.
В В-дереве вставка нового элемента возможна лишь в узел-лист. То есть вставленная новая пара ключ-значение добавляется лишь к узлу-листу. Вот, как осуществляется вставка в B-дерево:
Более подробную информацию всегда можно получить на наших курсах по алгоритмам в Москве:
Источник