Алгоритм Шеннона-Фано
Алгоритм метода Шеннона-Фано — один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано, и он имеет большое сходство с алгоритмом Хаффмана. Алгоритм основан на частоте повторения. Так, часто встречающийся символ кодируется кодом меньшей длины, а редко встречающийся — кодом большей длины.
В свою очередь, коды, полученные при кодировании, префиксные. Это и позволяет однозначно декодировать любую последовательность кодовых слов. Но все это вступление.
Для работы оба алгоритма должны иметь таблицу частот элементов алфавита.
- На вход приходят упорядоченные по невозрастанию частот данные.
- Выбираются две наименьших по частоте буквы алфавита, и создается родитель (сумма двух частот этих «листков»).
- Потомки удаляются и вместо них записывается родитель, «ветви» родителя нумеруются: левой ветви ставится в соответствие «1», правой «0».
- Шаг два повторяется до тех пор, пока не будет найден главный родитель — «корень».
- На вход приходят упорядоченные по невозрастанию частот данные.
- Находится середина, которая делит алфавит примерно на две части. Эти части (суммы частот алфавита) примерно равны. Для левой части присваивается «1», для правой «0», таким образом мы получим листья дерева
- Шаг 2 повторяется до тех пор, пока мы не получим единственный элемент последовательности, т.е. листок
Таким образом, видно, что алгоритм Хаффмана как бы движется от листьев к корню, а алгоритм Шеннона-Фано, используя деление, движется от корня к листям.
Ну вот, быстро осмыслив информацию, можно написать код алгоритма Шеннона-Фано на паскале. Попросили именно на нем написать. Поэтому приведу листинг вместе с комментариями.
program ShennonFano; uses crt; const a :array[1..6] of char = ('a','b','c','d','e','f'); < символы >af:array[1..6] of integer = (10, 8, 6, 5, 4, 3); < частота символов > < Процедура для поиска кода каждой буквы >procedure SearchTree(branch:char; full_branch:string; start_pos:integer; end_pos:integer); var dS:real; < Среднее значение массива >i, m, S:integer; < m - номер средней буквы в последовательности, S - сумма чисел, левой ветки >c_branch:string; < текущая история поворотов по веткам >begin < проверка если это вход нулевой то очистить историю >if (a<>' ') then c_branch := full_branch + branch else c_branch := ''; < Критерий выхода: если позиции символов совпали, то это конец >if (start_pos = end_pos) then begin WriteLn(a[start_pos], ' = ', c_branch); exit; end; < Подсчет среднего значения частоты в последовательности >dS := 0; for i:=start_pos to end_pos do dS:= dS + af[i]; dS := dS/2; < Тут какой угодно можно цикл for, while, repeat поиск середины >S := 0; i := start_pos; m := i; while ((S+af[i] SearchTree('1', c_branch, start_pos, m); < Правая ветка дерева >SearchTree('0', c_branch, m+1, end_pos); end; begin WriteLn('Press to show'); ReadLn; ClrScr; < Поиск кода Фано, входные параметры начало и конец последовательности >SearchTree(' ',' ', 1, 6); ReadLn; end; Ну вот собственно и все, о чем я хотел рассказать. Всю информацию можно взять из википедии. На рисунках приведены частоты сверху.
Источник
Префиксное кодирование
Наиболее простым методом получения кодов переменной длины является так называемое префиксное кодирование, которое позволяет получать целочисленные по длине коды. Главная особенность префиксных кодов заключается в том, что в пределах каждой их системы более короткие по длине коды не совпадают с началом (префиксом) более длинных кодов. Именно это свойство префиксных кодов позволяет очень просто производить декодирование информации.
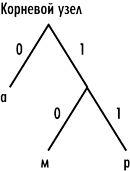
Поясним это свойство префиксных кодов на конкретном примере. Пусть имеется система из трех префиксных кодов: . Как видим, более короткий код 0 не совпадает с началом более длинных кодов 10 и 11. Пусть код 0 задает символ «а», код 10 — символ «м», а код 11 — символ «р». Тогда слово «рама» кодируется последовательностью 110100. Попробуем раскодировать эту последовательность. Поскольку первый бит — это 1, то первый символ может быть только «м» или «р» и определяется значением второго бита. Поскольку второй бит — это 1, то первый символ — это «р». Третий бит — это 0, и он однозначно соответствует символу «а». Четвертый бит — это 1, то есть нужно смотреть на значение следующего бита, который равен 0, тогда третий символ — это «м». Последний бит — это 0, что однозначно соответствует символу «а». Таким образом, свойство префиксных кодов, заключающееся в том, что более короткие по длине коды не могут совпадать с началом более длинных кодов, позволяет однозначно декодировать закодированное префиксными кодами переменной длины информационное сообщение.
Префиксные коды обычно получают построением кодовых (для двоичной системы) деревьев. Каждый внутренний узел такого бинарного дерева имеет два исходящих ребра, причем одному ребру соответствует двоичный символ «0», а другому — «1». Для определенности можно договориться, что левому ребру нужно ставить в соответствие символ «0», а правому — символ «1».
Поскольку в дереве не может быть циклов, от корневого узла к листовому всегда можно проложить один-единственный маршрут. Если ребра дерева пронумерованы, то каждому такому маршруту соответствует некоторая уникальная двоичная последовательность. Множество всех таких последовательностей будет образовывать систему префиксных кодов.
Для рассмотренного примера системы из трех префиксных кодов: , которые задают символы «а», «м» и «р», кодовое дерево показано на рис. 1.
Рис. 1. Кодовое дерево для системы из трех префиксных кодов:
Удобство древовидного изображения префиксных кодов заключается в том, что именно древовидная структура позволяет сформировать коды переменной длины, отвечающие главному условию префиксных кодов, то есть условию, что более короткие по длине коды не совпадают с началом более длинных кодов.
До сих пор мы рассматривали лишь идею префиксных кодов переменной длины. Что касается алгоритмов получения префиксных кодов, то их можно разработать достаточно много, но наибольшую известность получили два метода: Шеннона—Фано и Хаффмана.
Алгоритм Шеннона—Фано
Данный алгоритм получения префиксных кодов независимо друг от друга предложили Р. Фано и К. Шеннон, заключается он в следующем. На первом шаге все символы исходной информационной последовательности сортируются по убыванию или возрастанию вероятностей их появления (частоты их появления), после чего упорядоченный ряд символов в некотором месте делится на две части так, чтобы в каждой из них сумма частот символов была примерно одинакова. В качестве демонстрации рассмотрим уже знакомое нам слово «авиакатастрофа».
Если символы, составляющие данное слово, отсортировать по убыванию частоты их появления, то получим следующую последовательность: (в скобках указывается частота повторяемости символа в слове). Далее, нам нужно разделить эту последовательность на две части так, чтобы в каждой из них сумма частот символов была примерно одинаковой (насколько это возможно). Понятно, что раздел пройдет между символами «т» и «в», в результате чего образуется две последовательности: и . Причем суммы частот повторяемости символов в первой и второй последовательностях будут одинаковы и равны 7.
На первом шаге деления последовательности символов мы получаем первую цифру кода каждого символа. Правило здесь простое: для тех символов, которые оказались в последовательности слева, код будет начинаться с «0», а для тех, что справа — с «1».
Далее повторяем описанную процедуру для каждой из полученных таким делением последовательностей символов, поскольку каждая из них также упорядочена по частоте повторяемости символов.
В частности, последовательность разделится на два отдельных символа: a(5) и т(2) (других вариантов деления нет). Тогда вторая цифра кода для символа «a» — это «0», а для символа «т» — «1». Поскольку в результате деления последовательности мы получили отдельные элементы, то они более не делятся и для символа «a» получаем код 00, а для символа «т» — код 01.
В первом случае суммы частот повторяемости символов в первой и второй последовательностях будут 3 и 4 соответственно, а во втором случае — 4 и 3 соответственно. Для определенности воспользуемся первым вариантом.
Для символов полученной новой последовательности (это левая последовательность) первые две цифры кода будут 10, а для последовательности — 11.
Далее продолжаем описанную процедуру для каждой из полученных последовательностей до тех пор, пока в результате деления последовательностей в них будет оставаться не более одного символа.
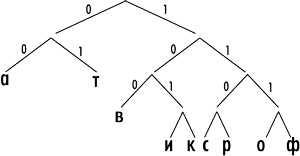
В нашем примере (рис. 2 и 3) получается следующая система префиксных кодов: «a» — 00, «т» — 01, «в» — 100, «и» — 1010, «к» — 1011, «с» — 1100, «р» — 1101, «о» — 1110, «ф» — 1111. Как нетрудно заметить, более короткие коды не являются началом более длинных кодов, то есть выполняется главное свойство префиксных кодов.
Рис. 2. Демонстрация алгоритма Шеннона—Фано на примере слова «авиакатастрофа»
Рис. 3. Кодовое дерево для слова «авиакатастрофа» в алгоритме Шеннона—Фано
Источник
Алгоритм вычисления кодов Шеннона-Фано
Код Шеннона-Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем.
Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.
При построении кода Шеннона-Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий.
Поэтому код Шеннона-Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона-Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона-Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
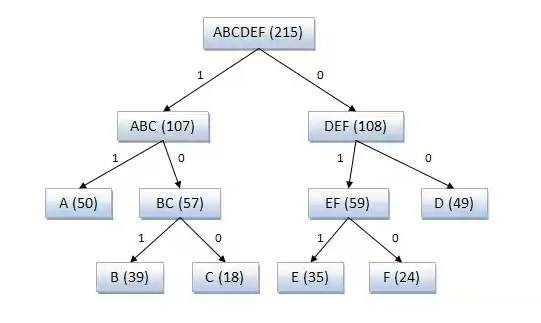
Пример кодового дерева
Исходные символы:
A (частота встречаемости 50)
B (частота встречаемости 39)
C (частота встречаемости 18)
D (частота встречаемости 49)
E (частота встречаемости 35)
F (частота встречаемости 24)
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
Кодирование Шеннона-Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона-Фано, поэтому более эффективным считается сжатие методом Хаффмана.
Пример 1. Закодируем буквы алфавита в коде Шеннона-Фано.
Пусть имеется случайная величина X (x1, x2, x3, x4, x5, x6, x7, x8), имеющая восемь состояний с распределением вероятностей
Для кодирования алфавита из восьми букв без учета вероятностей равномерным двоичным кодом нам понадобятся три символа:
Это 000, 001, 010, 011, 100, 101, 110, 111
Чтобы ответить, хорош этот код или нет, необходимо сравнить его с оптимальным значением, то есть определить энтропию
Определив избыточность L по формуле L=1-H/H0=1-2,75/3=0,084, видим, что возможно сокращение длины кода на 8,4%.
Все буквы записываются в порядке убывания их вероятностей, затем делятся на равновероятные группы, которые обозначаются 0 и 1, затем вновь делятся на равновероятные группы и т.д. (см.табл.4.1)
| X | P | Коды | |
| x1 | 1/4 | ——- | ——- |
| x2 | 1/4 | ——- | ——- |
| x3, | 1/8 | ——- | |
| x4 | 1/8 | ——- | |
| x5 | 1/16 | ||
| x6 | 1/16 | ||
| x7 | 1/16 | ||
| x8 | 1/16 |
Средняя длина полученного кода будет равна
Итак, мы получили оптимальный код. Длина этого кода совпала с энтропией. Данный код оказался удачным, так как величины вероятностей точно делились на равновероятные группы.
Возьмем 32 две буквы русского алфавита. Частоты этих букв известны. В алфавит включен и пробел, частота которого составляет 0,145. Метод кодирования представлен в таблице
| Буква | Рi | Код | ||
| ? | 0.145 | — | ||
| о | 0.095 | — | ||
| е | 0.074 | |||
| а | 0.064 | |||
| и | 0.064 | |||
| н | 0.056 | |||
| т | 0.056 | … | … | — |
| с | 0.047 | … | … | |
| . | … | |||
| ф | 0.03 |
Средняя длина данного кода будет равна, бит/букву;
Энтропия H=4.42 бит/буква. Эффективность полученного кода можно определить как отношение энтропии к средней длине кода. Она равна 0,994. При значении равном единице код является оптимальным. Если бы мы кодировали кодом равномерной длины , то эффективность была бы значительно ниже.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник