Кодовое дерево префиксного кода

Коды с минимальной

Пусть l = l (a 1 ,…, a r , p 1 ,…, p r) = inf l ср , где инфимум взят по всем однозначно декодируемым схемам. Пусть k = log q r . Тогда все a i можно закодировать разными словами длины k в алфавите B . Такое кодирование будет префиксным (а, следовательно, и взаимно однозначным). Отсюда l ≤ k. Таким образом, значение l достигается на некоторой схеме, так как для каждого i достаточно смотреть слова длины не более k/p i , p i >0.

Коды, определяемые схемами Σ с l ср = l , называются кодами с минимальной избыточностью или кодами Хаффмана. Каждому префиксному коду поставим в соответствие кодовое дерево — ориентированное корневое дерево T = T (Σ) по следующим правилам: •Множество вершин V(T) дерева T состоит из элементарных кодов и всех их префиксов, включая пустое слово. •Дуга в T ведет из C в D, если C является префиксом D и короче D ровно на одну букву.

Пусть T — кодовое дерево префиксного кода с минимальной избыточностью (со схемой Σ).

Можно считать, что p 1 ≥ … ≥ p r . Тогда можно преобразовать Σ таким образом, чтобы 1. i < j l i ≤ l j ; 2. порядки ветвления всех его вершин, за исключением быть может одной, лежащей в предпоследнем ярусе, равны или 0, или q; 3. порядок ветвления q 0 исключительной вершины ( если она есть) не равен

Если порядки ветвления всех вершин T равны или 0, или q, то положим q 0 = q. Ввиду (2), по индукции легко видеть, что для некоторого

целого t имеем r = t(q – 1) + q 0 . Следовательно,
если h —	– 1, то

Можно выбрать такой префиксный код с минимальной избыточностью, кодовое дерево которого кроме (1)–(3) обладает свойством 4. для некоторой вершины v, лежащей в предпоследнем ярусе, порядок ветвления вершины v равен q 0 , а потомками v являются a r ,a r−1 . a r−q0+1 .

Источник

Префиксное кодирование

Наиболее простым методом получения кодов переменной длины является так называемое префиксное кодирование, которое позволяет получать целочисленные по длине коды. Главная особенность префиксных кодов заключается в том, что в пределах каждой их системы более короткие по длине коды не совпадают с началом (префиксом) более длинных кодов. Именно это свойство префиксных кодов позволяет очень просто производить декодирование информации.

Поясним это свойство префиксных кодов на конкретном примере. Пусть имеется система из трех префиксных кодов: . Как видим, более короткий код 0 не совпадает с началом более длинных кодов 10 и 11. Пусть код 0 задает символ «а», код 10 — символ «м», а код 11 — символ «р». Тогда слово «рама» кодируется последовательностью 110100. Попробуем раскодировать эту последовательность. Поскольку первый бит — это 1, то первый символ может быть только «м» или «р» и определяется значением второго бита. Поскольку второй бит — это 1, то первый символ — это «р». Третий бит — это 0, и он однозначно соответствует символу «а». Четвертый бит — это 1, то есть нужно смотреть на значение следующего бита, который равен 0, тогда третий символ — это «м». Последний бит — это 0, что однозначно соответствует символу «а». Таким образом, свойство префиксных кодов, заключающееся в том, что более короткие по длине коды не могут совпадать с началом более длинных кодов, позволяет однозначно декодировать закодированное префиксными кодами переменной длины информационное сообщение.

Префиксные коды обычно получают построением кодовых (для двоичной системы) деревьев. Каждый внутренний узел такого бинарного дерева имеет два исходящих ребра, причем одному ребру соответствует двоичный символ «0», а другому — «1». Для определенности можно договориться, что левому ребру нужно ставить в соответствие символ «0», а правому — символ «1».

Поскольку в дереве не может быть циклов, от корневого узла к листовому всегда можно проложить один-единственный маршрут. Если ребра дерева пронумерованы, то каждому такому маршруту соответствует некоторая уникальная двоичная последовательность. Множество всех таких последовательностей будет образовывать систему префиксных кодов.

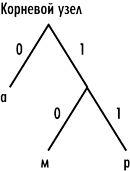
Для рассмотренного примера системы из трех префиксных кодов: , которые задают символы «а», «м» и «р», кодовое дерево показано на рис. 1.

Рис. 1. Кодовое дерево для системы из трех префиксных кодов:

Удобство древовидного изображения префиксных кодов заключается в том, что именно древовидная структура позволяет сформировать коды переменной длины, отвечающие главному условию префиксных кодов, то есть условию, что более короткие по длине коды не совпадают с началом более длинных кодов.

До сих пор мы рассматривали лишь идею префиксных кодов переменной длины. Что касается алгоритмов получения префиксных кодов, то их можно разработать достаточно много, но наибольшую известность получили два метода: Шеннона—Фано и Хаффмана.

Алгоритм Шеннона—Фано

Данный алгоритм получения префиксных кодов независимо друг от друга предложили Р. Фано и К. Шеннон, заключается он в следующем. На первом шаге все символы исходной информационной последовательности сортируются по убыванию или возрастанию вероятностей их появления (частоты их появления), после чего упорядоченный ряд символов в некотором месте делится на две части так, чтобы в каждой из них сумма частот символов была примерно одинакова. В качестве демонстрации рассмотрим уже знакомое нам слово «авиакатастрофа».

Если символы, составляющие данное слово, отсортировать по убыванию частоты их появления, то получим следующую последовательность: (в скобках указывается частота повторяемости символа в слове). Далее, нам нужно разделить эту последовательность на две части так, чтобы в каждой из них сумма частот символов была примерно одинаковой (насколько это возможно). Понятно, что раздел пройдет между символами «т» и «в», в результате чего образуется две последовательности: и . Причем суммы частот повторяемости символов в первой и второй последовательностях будут одинаковы и равны 7.

На первом шаге деления последовательности символов мы получаем первую цифру кода каждого символа. Правило здесь простое: для тех символов, которые оказались в последовательности слева, код будет начинаться с «0», а для тех, что справа — с «1».

Далее повторяем описанную процедуру для каждой из полученных таким делением последовательностей символов, поскольку каждая из них также упорядочена по частоте повторяемости символов.

В частности, последовательность разделится на два отдельных символа: a(5) и т(2) (других вариантов деления нет). Тогда вторая цифра кода для символа «a» — это «0», а для символа «т» — «1». Поскольку в результате деления последовательности мы получили отдельные элементы, то они более не делятся и для символа «a» получаем код 00, а для символа «т» — код 01.

В первом случае суммы частот повторяемости символов в первой и второй последовательностях будут 3 и 4 соответственно, а во втором случае — 4 и 3 соответственно. Для определенности воспользуемся первым вариантом.

Для символов полученной новой последовательности (это левая последовательность) первые две цифры кода будут 10, а для последовательности — 11.

Далее продолжаем описанную процедуру для каждой из полученных последовательностей до тех пор, пока в результате деления последовательностей в них будет оставаться не более одного символа.

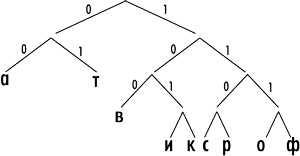
В нашем примере (рис. 2 и 3) получается следующая система префиксных кодов: «a» — 00, «т» — 01, «в» — 100, «и» — 1010, «к» — 1011, «с» — 1100, «р» — 1101, «о» — 1110, «ф» — 1111. Как нетрудно заметить, более короткие коды не являются началом более длинных кодов, то есть выполняется главное свойство префиксных кодов.

Рис. 2. Демонстрация алгоритма Шеннона—Фано на примере слова «авиакатастрофа»

Рис. 3. Кодовое дерево для слова «авиакатастрофа» в алгоритме Шеннона—Фано

Источник

Префиксные коды

Однозначность декодирования можно обеспечить, не вводя разделительного символа, если строить код так, чтобы он удовлетворял условию, известному под названием «свойство префикса». Оно заключается в том, что ни одна комбинация более кратного кода не должна совпадать с началом («префиксом») другого кодового слова. Коды, удовлетворяющие этому условию, называют префиксными кодами. Эти коды обеспечивают однозначное декодирование принятых кодовых слов без введения дополнительной информации для их разделения, т. е. всякая последовательность кодовых символов должна быть единственным образом разделена на кодовые слова. Коды, в которых это требование выполнимо, называются однозначно декодируемыми, или кодами без запятой.

Если код префиксный, то, читая принятую последовательность подряд с начала до конца, можно установить, где кончается одно кодовое слово и начинается следующее. Например, если код префиксный и в последовательности встретился код 110, то, очевидно, в коде не должно содержаться слов (1), (11). Закодировано префиксным кодом с а₁ = (00), а₂ =(01), а₃ = (101), а₄ = (100). На рис. 1 представлен граф (кодовое дерево) префиксного кода с сообщениема₁ = (0), а₂ =(1), а₃ = (11), а₄ = (111). Из рис. 1 следует, что если свойство префикса не выполняется, то некоторые промежуточные вершины дерева могут соответствовать кодовым словам.

Рис. Кодовое слово непрефиксного кода

Примерами префиксных кодов являются коды Шеннона-Фано и Хаффмана. Код Шеннона-Фано

Сообщения алфавита источника выписывают в порядке убывания вероятностей их появления. Далее разделяют их на две части так, чтобы суммарные вероятности сообщений в каждой из этих частей были по возможности почти одинаковыми. Припишем сообщениям первой части в качестве первого символа – 0, а второй – 1 (можно наоборот). Затем каждая из этих частей (если она содержит более одного сообщения) делится на две по возможности равновероятные части, и в качестве второго символа для первой из них берется 0, а для второй – 1. Этот процесс повторяется, пока в каждой из полученных частей не останется по одному сообщению.

Рис. Кодовое дерево кода Шеннона – Фано

Методика Шеннона – Фано не всегда приводит к однозначному построе­нию кода, поскольку при разбиении на части можно сделать больше по веро­ятности как верхнюю, так и нижнюю части. Кроме того, методика не обеспе­чивает отыскания оптимального множества кодовых слов для кодирования данного множества сообщений. (Под оптимальностью подразумевается то, что никакое другое однозначно декодируемое множество кодовых слов не имеет меньшую среднюю длину кодового слова, чем заданное множество.) Предложенная Хаффманом конструктивная методика свободна от отмечен­ных недостатков.

Код Хаффмана

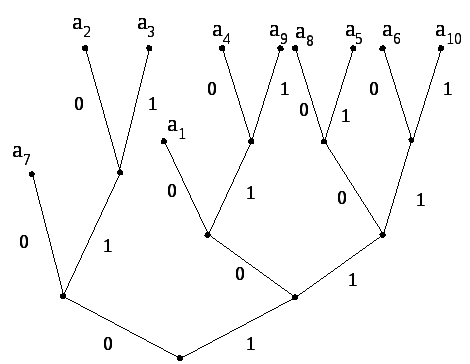
Буквы алфавита сообщений выписывают в основной столбец таблицы кодирования в порядке убывания вероятностей. Две последние буквы объединяют в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятность букв, не участвовавших в объединении, и полученная суммарная вероятность слова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяют. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Для нахождения кодовой комбинации необходимо проследить путь перехода знака по строкам и столбцам таблицы. Это наиболее наглядно осуществимо по кодовому дереву. Из точки, соответ­ствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваиваем символ 1, а с меньшей – 0. Такое последователь­ное ветвление продолжается до тех пор, пока не дойдем до вероятности каж­дой буквы. Двигаясь по кодовому дереву сверху вниз, можно записать для каждого сообщения соответствующие ему кодовые комбинации.

Рис. Кодовое дерево кода Хаффмана

Источник