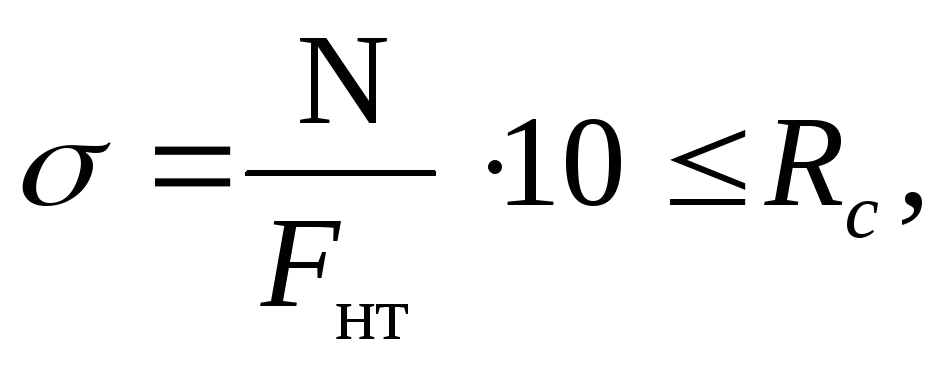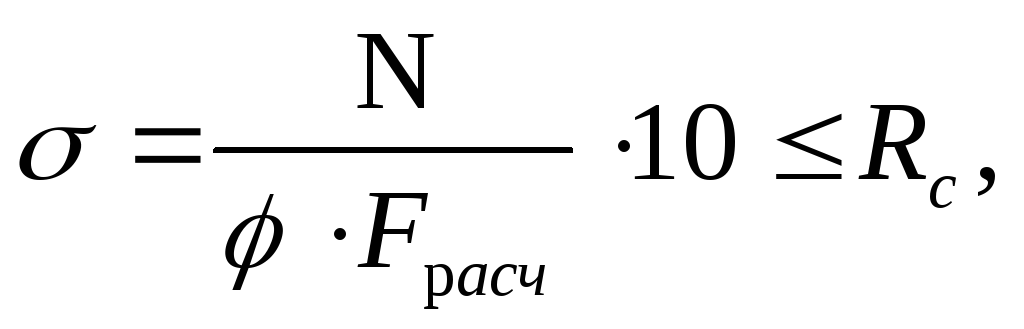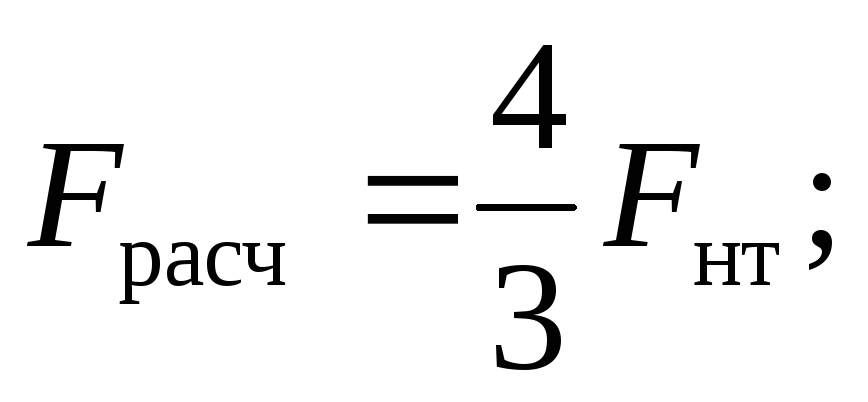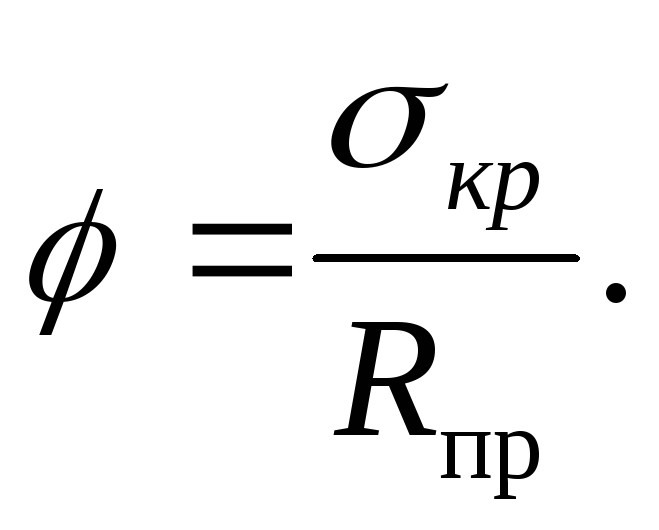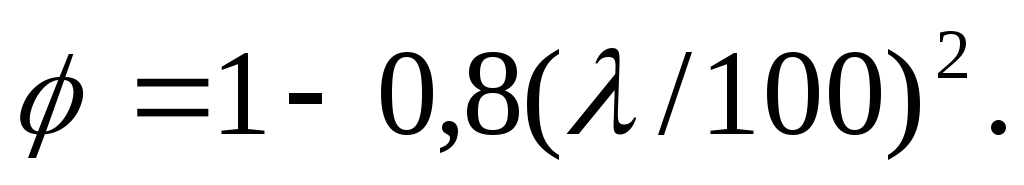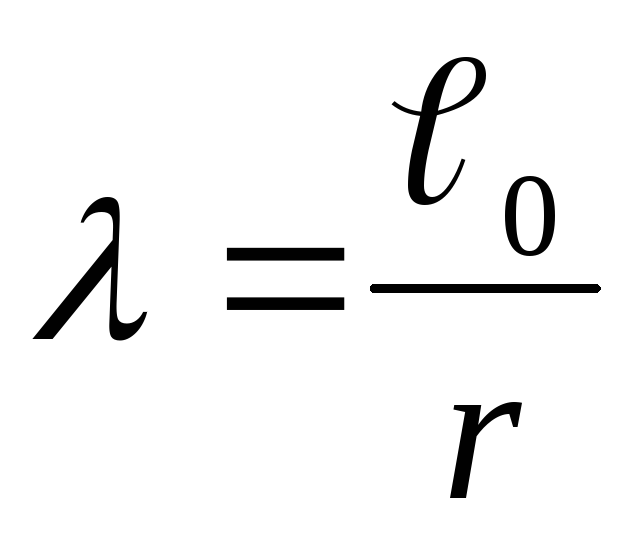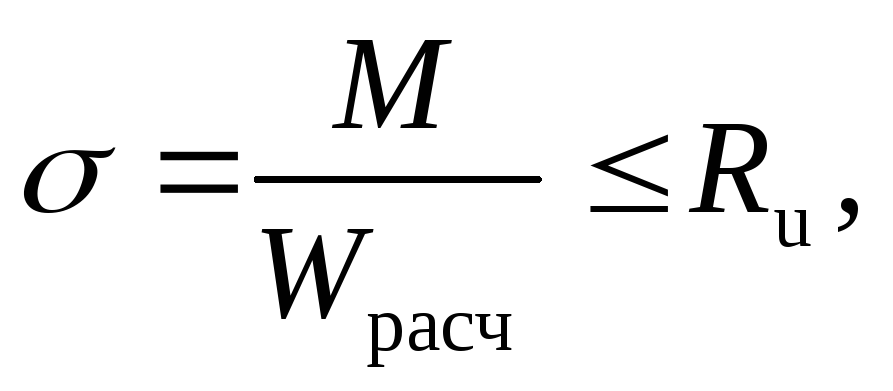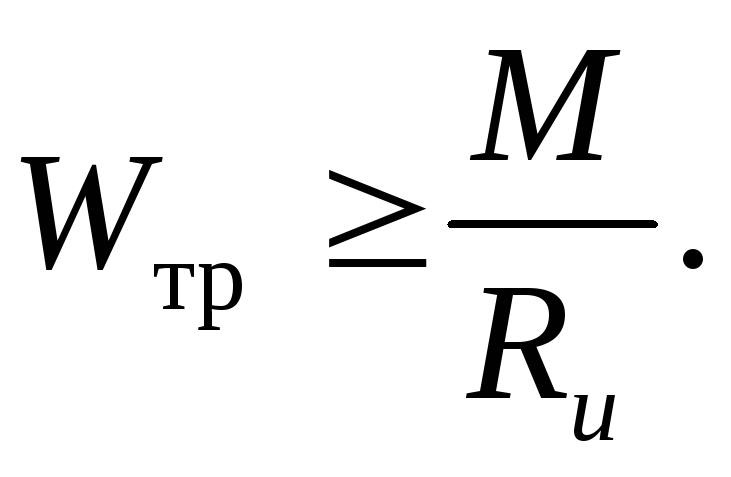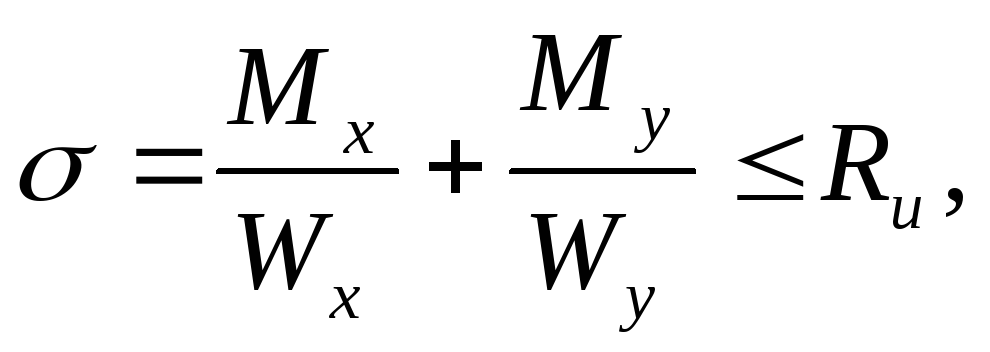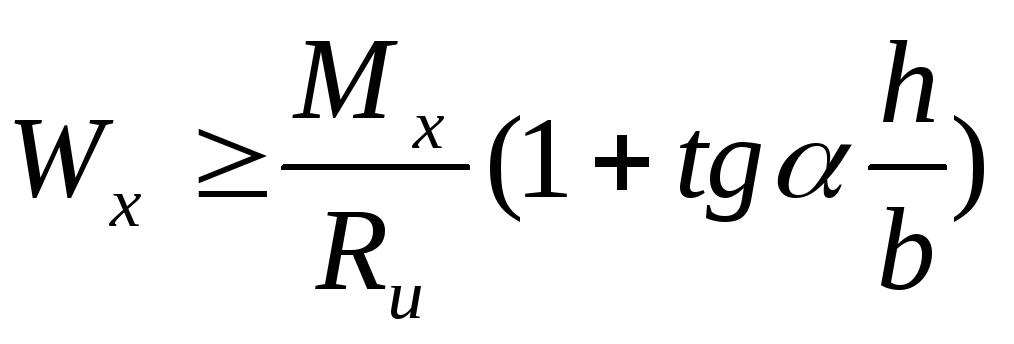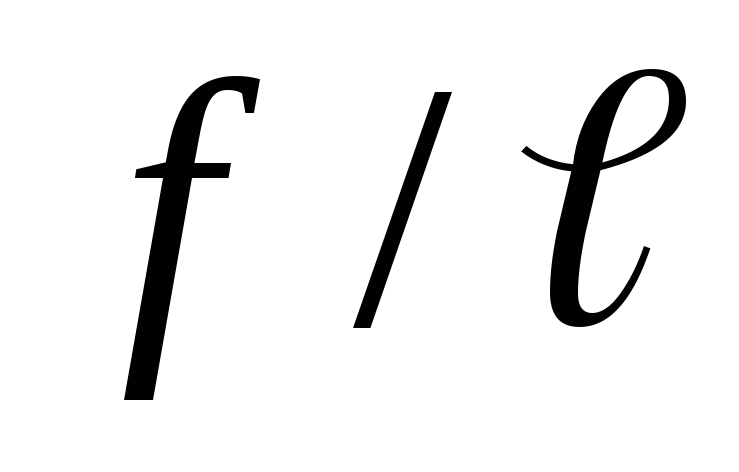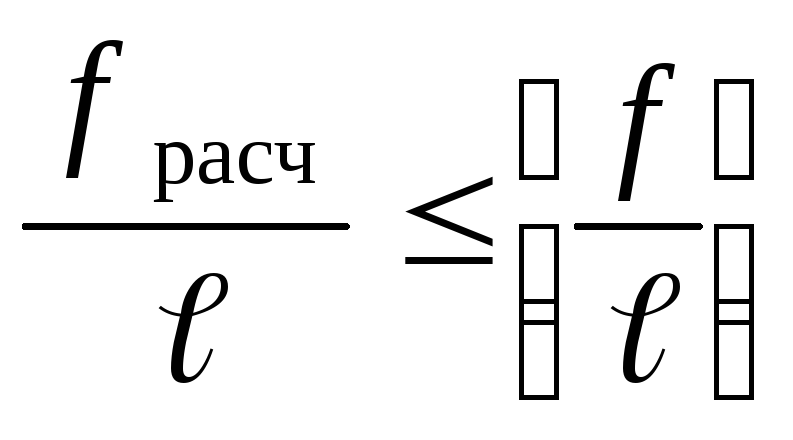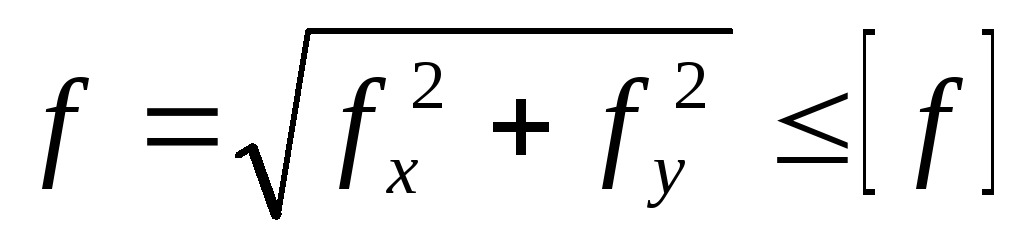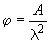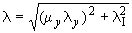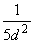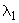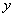1. Расчет центрально сжатых и изгибаемых деревянных элементов
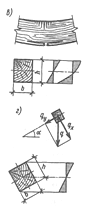
На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм (рис. 3.3).
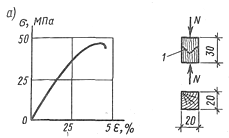
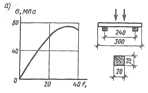
Рис. 3.3. Сжатый элемент:
а — график деформаций и образец; б — схемы работы, разрушения и эпюра
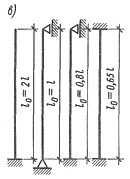
напряжений; в — типы закрепления концов и расчетные длины; г—график
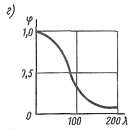
коэффициентов устойчивости φ в зависимости от гибкости λ.
Разрушение центрально сжатых элементов может произойти от потери устойчивости или прочности.
Центрально сжатые элементы рассчитывают по формулам:
где N – расчётное сжимающее усилие;
F=(Fбр-Fосл), как для растянутых элементов;
Fрасч – расчётная площадь поперечного сечения при проверке устойчивости.
Принимается равной Fбр – при отсутствии ослаблений;
при ослаблениях, не выходящих на кромку, если площадь ослаблений Fосл≤0,25Fбр, то Fрасч= Fбр;
при симметричных ослаблениях, выходящих на кромки Fрасч= Fнт.
При несимметричных ослаблениях, выходящих на кромку, элементы рассчитываются как внецентренно сжатые.
Коэффициент продольного изгиба φ – отношение критического напряжения, при котором стержень теряет устойчивость, к пределу прочности материала на сжатие.
Коэффициент φ обычно меньше 1, зависит от гибкости стержня λ. При λ>λmin, коэффициент φ находится по формуле Эйлера:
Гибкость элементов λ определяют в зависимости от их расчётной длины и радиуса инерции поперечного сечения по формуле:
Расчётная длина зависит от способа закрепления элемента и равна .
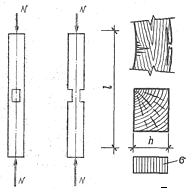
На изгиб работают настилы, обрешётки, обшивки плит и панелей, стропильные ноги, прогоны, балки (рис. 3.4).
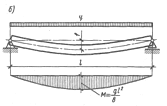
Рис. 3.4. Изгибаемый элемент:
а — график прогибов и образец; б — схема работы и эпюры изгибающих моментов; в — схема разрушения и эпюры нормальных напряжений; г — схема работы при косом изгибе и эпюра напряжений
Изгибаемые элементы рассчитываются на прочность и жёсткость (по деформациям или прогибам), т.е. по двум предельным состояниям. Различают два вида работы элементов на изгиб: простой изгиб, когда нагрузка действует в плоскости одной из главных осей инерции поперечного сечения элемента; косой изгиб, когда направление нагрузки не совпадает ни с одной из главных осей инерции сечения (рис. 3.4, б).
Изгибаемые элементы на прочность при простом изгибе рассчитываются по формуле:
где Wрасч – расчётный момент сопротивления по площади нетто. Для клееных (гнутых) деревянных элементов
для составных стержней на податливых связях
При простом изгибе сечение по заданному изгибающему моменту М подбираются по формуле:
По найденному моменту сопротивления находят размеры поперечного сечения и подбирают пиломатериал по сортаменту, например для прямоугольного сечения.
При косом изгибе (рис. 3.4, г) расчёт элементов на прочность по нормальным напряжениям производится по формуле:
Мх и Мy– составляющие расчётного изгибающего момента относительно главных осей x и y,
Wx и Wy – расчётные моменты сопротивления поперечного сечения нетто для осей х и y,
Ru – расчётное сопротивление изгибу.
Для подбора прямоугольного сечения косоизгибаемого элемента можно пользоваться формулами:
Проверка на скалывание производится по формуле Журавского:
Прогибы вычисляются как относительная величина в предположении упругой работы древесины по формулам сопротивления материалов в соответствии с расчётными схемами. Необходимо выполнение условия:
Прогиб элементов с учётом воздействия касательных напряжений определяют по формуле:
f0— прогиб без учёта касательных напряжений;
k — коэффициент, зависящий от схемы нагружения внешней нагрузкой;
β- коэффициент, зависящий от формы поперечного сечения и коэффициента Пуассона (μ) материала балки.
Полный пролёт балки при косом изгибе равен геометрической сумме прогибов 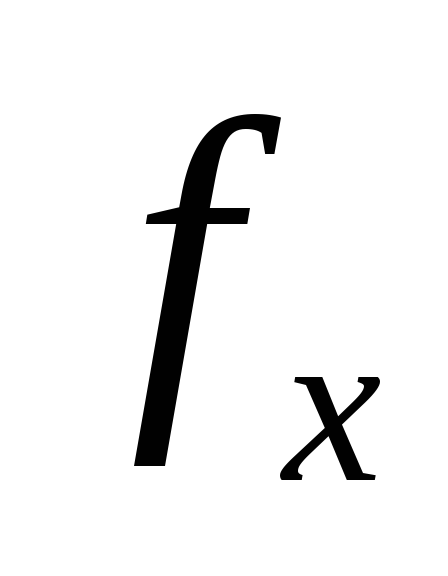
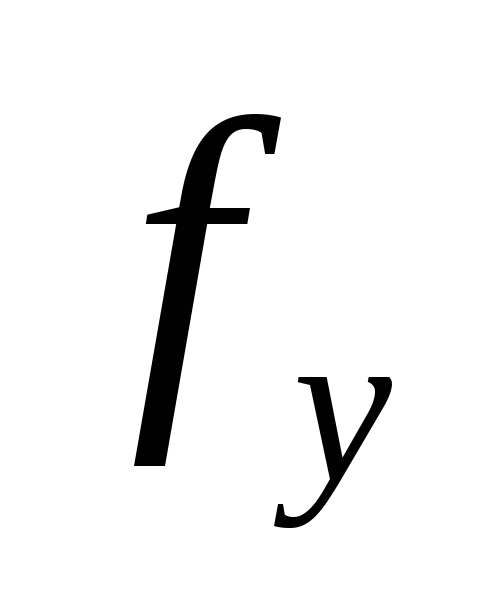

Косой изгиб существенно увеличивает размеры прямоугольного сечения (прогонов), поэтому следует конструктивными мероприятиями добиваться того, чтобы основная нагрузка действовала в плоскости наибольшей жёсткости.
Наименьшая площадь поперечного сечения прямоугольного прогона при косом изгибе из условия прочности получается при соблюдении отношения:
при
Источник
Коэффициент продольного изгиба дерева
Величины модулей упругости и сдвига строительной фанеры в плоскости листа 


5.4 При расчете по предельным состояниям первой группы по деформированной схеме модули упругости и сдвига следует принимать согласно 5.3 с умножением на коэффициент , равный 0,75 — для древесины и 0,8 — для LVL.
5.5 Модули упругости древесины, LVL и фанеры для конструкций, находящихся в различных условиях эксплуатации, подвергающихся воздействию повышенной температуры, совместному воздействию постоянной и временной длительной нагрузок, следует определять умножением указанных выше величин Е и G на коэффициент 


5.6 Модуль упругости древесины, LVL и фанеры в расчетах конструкций (кроме опор ЛЭП) на устойчивость следует принимать равным для древесины 


для фанеры — 



Модуль упругости , МПа
Модуль сдвига , МПа
Коэффициент Пуассона
Источник
6 Расчет элементов деревянных конструкций


где — расчетная продольная сила;
— расчетное сопротивление древесины растяжению вдоль волокон;
— то же, для древесины из однонаправленного шпона (5.7);
— площадь поперечного сечения элемента нетто.
При определении ослабления, расположенные на участке длиной до 200 мм, следует принимать совмещенными в одном сечении.
6.2Расчетцентрально-сжатыхэлементовпостоянного цельного сеченияследует производить по формулам:




где — расчетное сопротивление древесины сжатию вдоль волокон;
— то же, для древесины из однонаправленного шпона;
— коэффициент продольного изгиба, определяемый согласно 6.3;
— площадь нетто поперечного сечения элемента;
— расчетная площадь поперечного сечения элемента, принимаемая равной:
при отсутствии ослаблений или ослаблениях в опасных сечениях, не выходящих на кромки (рисунок 1, а), если площадь ослаблений не превышает 25%





а— не выходящие на кромку;б— выходящие на кромку
Рисунок 1— Ослабление сжатых элементов
6.3Коэффициент продольного изгибаследует определять по формулам:
при гибкости элемента 70
; (7)
при гибкости элемента 70
, (8)
где коэффициент 

коэффициент 

6.4Гибкость элементов цельного сечения определяют по формуле
, (9)
где — расчетная длина элемента;


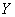
6.5Расчетную длину элемента

(10)
6.6Составные элементы на податливых соединениях, опертые всем сечением, следует рассчитывать на прочность и устойчивость по формулам (8) и (9), при этом

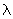
, (11)*
где 





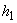

— коэффициент приведения гибкости, определяемый по формуле
* Формула и экспликация к ней соответствуют оригиналу. — Примечание изготовителя базы данных.
, (12)
где 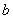

— расчетное число швов в элементе, определяемое числом швов, по которым суммируется взаимный сдвиг элементов (на рисунке 2,а— 4 шва, на рисунке 2,б— 5 швов);
— расчетная длина элемента, м;
— расчетное число срезов связей в одном шве на 1 м элемента (при нескольких швах с различным числом срезов следует принимать среднее для всех швов число срезов);
— коэффициент податливости соединений, который следует определять по формулам таблицы 15.
а— с прокладками,б— без прокладок
Рисунок 2— Составные элементы
Коэффициент при
2 Стальные цилиндрические нагели
а) диаметром толщины соединяемых элементов
б) диаметром толщины соединяемых элементов
3 Вклеенные стержни из арматуры А240-А500
4 Дубовые цилиндрические нагели
5 Дубовые пластинчатые нагели
Примечание — Диаметры гвоздей, шурупов, нагелей и вклеенных стержней 



При определении 



При определении диаметр дубовых цилиндрических нагелей следует принимать не более 0,25 толщины более тонкого из соединяемых элементов.
Связи в швах следует расставлять равномерно по длине элемента. В шарнирно-опертых прямолинейных элементах допускается в средних четвертях длины ставить связи в половинном количестве, вводя в расчет по формуле (12) величину , принятую для крайних четвертей длины элемента.
Гибкость составного элемента, вычисленную по формуле (11), следует принимать не более гибкости отдельных ветвей, определяемой по формуле:
, (13)
где 

— площадь сечения брутто элемента;
— расчетная длина элемента.
Гибкость составного элемента относительно оси, проходящей через центры тяжести сечений всех ветвей (ось на рисунке 2), следует определять как для цельного элемента, т.е. без учета податливости связей, если ветви нагружены равномерно. В случае неравномерно нагруженных ветвей следует руководствоваться 6.7.
Если ветви составного элемента имеют различное сечение, то расчетную гибкость ветви в формуле (11) следует принимать равной
, (14)
определение приведено на рисунке 2.
6.7Составные элементы на податливых соединениях, часть ветвей которых не оперта по концам, допускается рассчитывать на прочность и устойчивость по формулам (5), (6) при соблюдении следующих условий:
а) площади поперечного сечения элемента 

б) гибкость элемента относительно оси (см. рисунок 2) определяется по формуле (11); при этом момент инерции принимается с учетом всех ветвей, а площадь — только опертых;
в) при определении гибкости относительно оси (см. рисунок 2) момент инерции следует определять по формуле
, (15)
где 

6.8Расчет на устойчивость центрально-сжатых элементов переменного по высоте сечения следует выполнять по формуле


где — площадь поперечного сечения брутто с максимальными размерами;


— коэффициент продольного изгиба, определяемый по 6.3 для гибкости, соответствующей сечению с максимальными размерами.
Источник