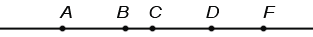Комбинаторные задачи дерево возможных вариантов

Комбинаторные задачи

Комбинаторика (от латинского слова combinare, означающего №соединять», «сочетать») — это область математики, которая изучает способы выбора, расположения, сочетания различных объектов. Решение задач в данном разделе математики требует рассмотрения и подсчёта всех возможных комбинаций (отсюда название комбинаторные задачи). Решая эти задачи, обычно надо отвечать на вопрос «Сколькими способами. » или «Сколько вариантов. «

Задача: Нам даны фигуры: треугольник, овал и прямоугольник . Необходимо построить пирамидку, состоящую из трех разных фигур. Сколькими способами это можно сделать?

Метод перебора

Данный метод удобен при небольшом числе вариантов. Решение в данном случае происходит путём перебора всех возможных вариантов. При этом очень важно выбрать правильный вариант перебора — логику перебора.

Воспользуемся методом перебора: Пусть в основании пирамидки находится прямоугольник, тогда возможны варианты построения: прямоугольник — овал — треугольник и прямоугольник — треугольник — овал.

Теперь в основании положим овал, тогда возможны варианты построения: овал — прямоугольник — треугольник и овал — треугольник — прямоугольник.

Теперь в основании положим треугольник, тогда возможны варианты построения: треугольник — прямоугольник — овал и треугольник — овал — прямоугольник.

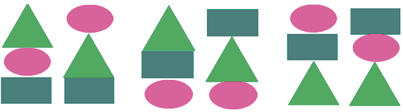
Итак, мы получили шесть возможных вариантов:

Ответ: 6 способов.

При решении данной задачи мы изображали фигуры, но для упрощения решения можно использовать кодирование. Данный прием позволяет заметить фигуры, например, первыми буквами их названия, то есть овал обозначаем буквой О, треугольник — Т, прямоугольник — П. Тогда решение будет выглядеть так:

Дерево возможных вариантов

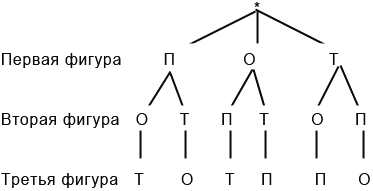
Данный метод заключается в построении схемы, которая и называется деревом возможных вариантов. Данная схема действительно похожа на перевернутое дерево, «корень» которого обозначается «*». Построим данную схему для нашей задачи: Для этого от «корня» проведем три «ветки» — отрезки, на концах которых подпишем варианты фигур, которые мы можем взять за основание. Далее от каждой фигуры проводим такое количество «веток», которое будет соответствовать числу вариантов фигур на втором месте, в нашем случае по две «ветки» от каждой фигуры. Затем от каждой фигуры, стоящей на втором месте, проводим такое число «веток», которое будет соответствовать числу вариантов фигур на третьем месте, в нашем случае по одной «ветке» от каждой фигуры. Тогда имеем следующее дерево возможных вариантов:

Метод отрезков

Данный метод используется только для составления всевозможных пар. Например, рассмотрим прямую, на которой обозначены точки A, B, C, D, F:

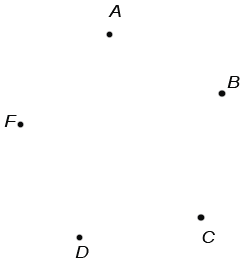
Необходимо ответить на вопрос: » Сколько отрезков изображено на рисунке?». Мы знаем, что отрезок обозначается двумя буквами, значит, для ответа на вопрос необходимо перебрать всевозможные пары букв. Это можно сделать при помощи следующей схемы: Отметим точки так, чтобы никакие 3 не лежали на одной прямой:

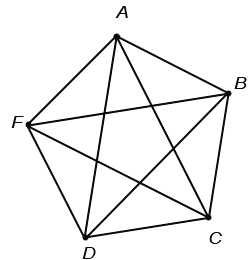
Соединим данные точки отрезками между собой. Число отрезков будет числом вариантов, то есть числом отрезков, изображенных на рисунке:

Итак, мы получили 10 отрезков, соединяющих точки.

Ответ: На рисунке 10 отрезков.

Источник

Методы решения комбинаторных задач

Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.

Задача 1.
Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?

Ответ: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.

Задача 2.
В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.

Ответ:
Вариант 1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант 2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант 3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант 4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант 5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант 6: 1) Громов, 2) Иванов, 3) Орлов.

Задача 3.
В кружок бального танца записались Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?

Ответ:
1) Таня — Петя, 2) Таня — Коля, 3) Таня — Витя, 4) Таня — Олег, 5) Оля — Петя, 6) Оля — Коля, 7) Оля — Витя, 8) Оля — Олег, 9) Наташа — Петя, 10) Наташа — Коля, 11) Наташа — Витя, 12) Наташа — Олег, 13) Света — Петя, 14) Света — Коля, 15) Света — Витя, 16) Света — Олег.

Дерево возможных вариантов

Самые разные комбинаторные задачи решаются с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда и название метода — дерево возможных вариантов.

Задача 4.
Какие трехзначные числа можно составить из цифр 0, 2, 4?

Решение. Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе.

Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.

Задача 5.
Школьные туристы решили совершить путешествие к горному озеру. Первый этап пути можно преодолеть на поезде или автобусе. Второй этап — на байдарках, велосипедах или пешком. И третий этап пути — пешком или с помощью канатной дороги. Какие возможные варианты путешествия есть у школьных туристов?

Решение. Построим дерево возможных вариантов, обозначив путешествие на поезде П, на автобусе — А, на байдарках — Б, велосипедах — В, пешком — Х, на канатной дороге — К.

Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов.

Задача 6.
Запишите все возможные варианты расписания пяти уроков на день из предметов: математика, русский язык, история, английский язык, физкультура, причем математика должна быть вторым уроком.

Решение. Построим дерево возможных вариантов, обозначив М — математика, Р — русский язык, И — история, А — английский язык, Ф — физкультура.

Ответ: Всего 24 возможных варианта:

Источник

Решение комбинаторных задач

Презентация по теме «Решение комбинаторных задач» для самостоятельного изучения темы.

Просмотр содержимого документа
«Решение комбинаторных задач»

Решение комбинаторных задач

Комбинаторные задачи – это задачи, в которых требуется из элементов составить различные наборы, подсчитать количество всевозможных комбинаций элементов, составленных по определённому правилу.

Методы решения комбинаторных задач

1. Метод перебора вариантов

2. Дерево возможных вариантов

Метод перебора вариантов

Полный перебор вариантов без составления таблиц и схем

Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5?

Перебираем всевозможные варианты: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.

В финальном забеге на 100 м участвуют Смирнов, Петров и Орлов. Назовите возможные варианты распределения призовых мест.

Задача 1: Вариант1: 1) Смирнов, 2) Петров, 3) Орлов. Вариант2: 1) Смирнов, 2) Орлов, 3) Петров. Вариант3: 1) Орлов, 2) Смирнов, 3) Петров. Вариант4: 1) Орлов, 2) Петров, 3) Смирнов. Вариант5: 1) Петров, 2) Орлов, 3) Смирнов. Вариант6: 1) Петров, 2) Смирнов, 3) Орлов .

Дерево возможных вариантов

способ решения разнообразных задач, касающихся перебора вариантов происходящих событий.

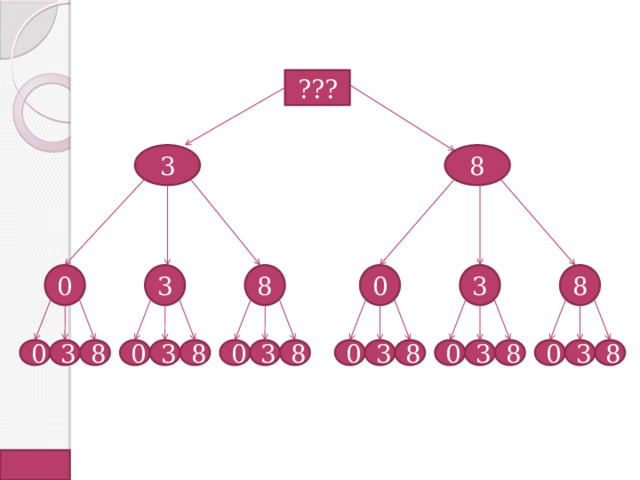
Какие трехзначные числа можно составить из цифр 0, 3, 8?

Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе.

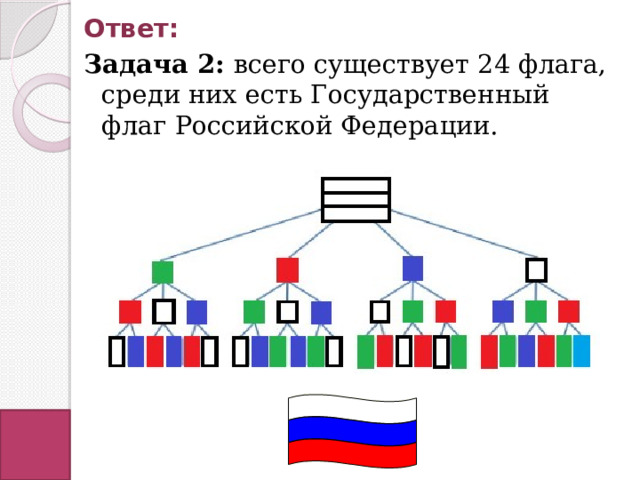
Сколько существует флагов составленных из трех горизонтальных полос одинаковой ширины и различных цветов: белого, синего, красного и зеленого? Есть ли среди них Государственный флаг Российской Федерации?

Задача 2: всего существует 24 флага, среди них есть Государственный флаг Российской Федерации.

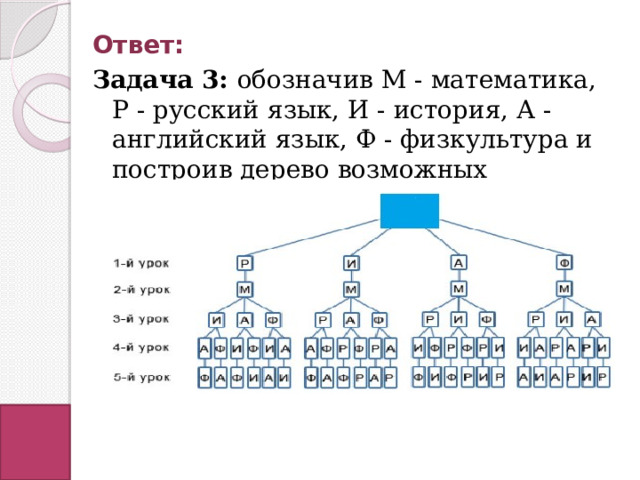
Запишите все возможные варианты расписания пяти уроков на день из предметов: математика, русский язык, история, английский язык, физкультура, причем математика должна быть вторым уроком.

Задача 3: обозначив М — математика, Р — русский язык, И — история, А — английский язык, Ф — физкультура и построив дерево возможных вариантов, получим всего 24 варианта .

Решить комбинаторные задачи можно с помощью таблиц. Они, как и дерево возможных вариантов, наглядно представляют решение таких задач.

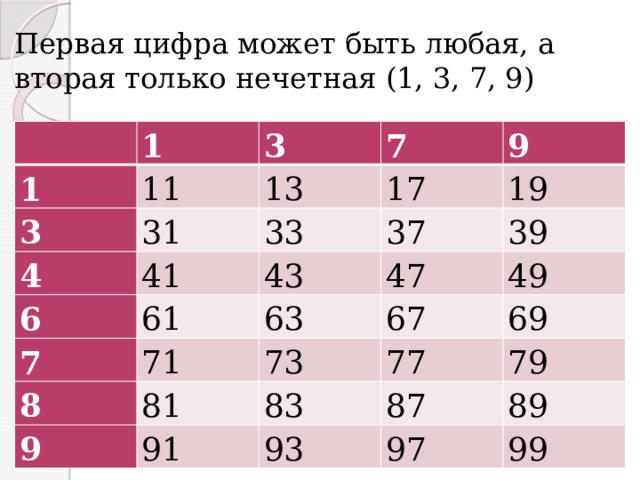
Задача 1. Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9?

Решение. Составим таблицу: слева первый столбец — первые цифры искомых чисел, вверху первая строка — вторые цифры.

Первая цифра может быть любая, а вторая только нечетная (1, 3, 7, 9)

Источник

Уроки математики и физики для школьников и родителей

Составляя комбинации, мы фактически выбираем из этого множества различные элементы и объединяем их в группы по нашим потребностям, поэтому вместо слова “комбинаторика”, часто используют слово “выборки” элементов.

Комбинаторная задача – задача, требующая осуществления перебора всех возможных вариантов или подсчёта их числа.

У Маши имеются юбка с брюками и кофта, свитер, рубашка. Сколько комплектов можно составить из этой одежды ?

Табличный метод (все условия вносятся в таблицу, в ней же выполняется решение).

Составим таблицу : слева первый столбец – первые цифры искомых чисел, вверху первая строка вторые цифры.

Составим таблицу : слева первый столбец – первые цифры искомых чисел, вверху первая строка вторые цифры.

Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.

Составим таблицу : слева первый столбец – имена девочек, вверху первая строка – имена мальчиков.

Объекты представляются как вершины , или узлы графа , а связи – как дуги , или рёбра .

Встретились пятеро друзей, как положено, поздоровались друг с другом. Сколько рукопожатий было сделано ?

Постройте отрезок АВ , и отметьте на нём 4 точки М, С. К, Д . Определите с помощью грф – схемы количество отрезков.

ОТВЕТ: 15 .

При построении граф-схем кроме дуг и вершин используется петля. она используется в случаях, когда требуется показать, что число делится само на себя.

ЗАДАЧА:

Выберите граф, на котором показано, что одно число делится на другое и на само себя.

Самые разные комбинаторные задачи решаются с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда и название – дерево возможных вариантов .

Дерево возможных вариантов – граф, схема, отражающая структуру задачи, упорядочения многошагового процесса принятия решений.

Ветви дерева отображают различные события, которые могут иметь место, а корень дерева – состояние, в котором возникает необходимость выбора.

Запишите все трёхзначные числа, которые можно составить из цифр 1, 2, 3 , так, чтобы числа не повторялись.

РЕШЕНИЕ: ЗАДАЧА:

Катя, Лена и Соня сегодня дежурные. Им нужно расставить книги (К) , вымыть пол (П) , полить цветы (Ц) . Сколькими способами они могут распределить между собой обязанности ?

Построим дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе .

Имеются три слова “ДРУЖБА”, “ДЕЛО”, “ЛЮБИТ”. Сколькими способами из этих слов можно составить фразу ?

Комментариев нет:

Отправить комментарий

Уроки математики и физики (RU + UA)

• I. НАТУРАЛЬНЫЕ ЧИСЛА И ДРОБИ (RU + UA + EN)
• II. ПРОПОРЦИИ ПРОЦЕНТЫ МАСШТАБ (RU + UA)
• III. РАЦИОНАЛЬНЫЕ ЧИСЛА (RU + UA)
• IV. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ (RU + UA)
• V. КОРНИ (RU + UA)
• VI. ФУНКЦИИ И ГРАФИКИ (RU + UA + EN)
• VII. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ (RU + UA)
• VIII. ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
• IX. НЕРАВЕНСТВА (RU + UA)
• X. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ (RU + UA)
• XI. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА (RU + UA)
• XII. ПЛАНИМЕТРИЯ (1) (RU + UA)
• XIII. ПЛАНИМЕТРИЯ (площади фигур) (RU + UA)
• XIV. СТЕРЕОМЕТРИЯ (1) (RU + UA)
• XV. СТЕРЕОМЕТРИЯ (2) (RU + UA)
• XVI. КОМБИНАТОРИКА (RU + UA)
• XVII. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ (RU + UA)
• XVIII. ВЕКТОРЫ (RU + UA)
• XIX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И СТАТИСТИКИ (RU + UA)
• XX. ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ (RU + UA)
• КИНЕМАТИКА
• ДИНАМИКА
• WATCH YOUR MONEY!

О сайте

На сайте размещена минимальная информация по математике, позволяющая сдать тесты любому ученику с положительной отметкой, если конечно он решит все предложенные уроки.
Также данный сайт поможет ученику, начинающему изучать математику и бабушкам, которые захотят помочь своим внукам в изучении математики.

Каждый урок содержит краткие сведения по теоретической части и три практических задания по 12 примеров или задач в каждом задании. При желании Вы можете написать ответы заданий для проверки в комментариях. Сайт находится в постоянной доработке. Возможны методические и математические ошибки.

Автор блога

Евгений Красавцев

Популярные статьи за последние 7 дней

Источник