Кому показано дерево элементов

Что такое дерево проектирования элементов в Solidworks?

Щелкните правой кнопкой мыши в дереве конструирования FeatureManager и выберите Отображение дерева > Показать плоское представление дерева. В представлении Flat Tree View кривые, 2D-эскизы и 3D-эскизы не поглощаются элементами, которые на них ссылаются. Вместо этого они показаны в порядке создания.

Каковы основные или основные компоненты дерева конструирования FeatureManager?

Дерево конструирования FeatureManager в сборке

• Сборка верхнего уровня (первый пункт)
• Различные папки, например Аннотации и Сопряжения.
• Сборочные плоскости и происхождение.
• Компоненты (узлы и отдельные детали)
• Элементы сборки (вырезы или отверстия) и массивы компонентов.
• Сгруппированные компоненты.

Как вернуть дерево проектирования в SOLIDWORKS?

Можно выбрать параметры отображения для дерева конструирования FeatureManager. Чтобы получить доступ к этим параметрам, щелкните правой кнопкой мыши имя детали или сборки в дереве конструирования FeatureManager и выберите Отображение дерева.

Что такое дерево дизайна?

Эта палитра помогает дизайнеру найти любой используемый объект дизайна в файле дизайна. Это всеобъемлющее устройство выбора, использующее дерево папок, подобное проводнику Windows, позволяющее находить все, от аппаратных устройств до отдельных элементов управления на панелях управления.

Как переместить дерево элементов в SOLIDWORKS?

Вы можете изменить порядок перестроения элементов, перетащив их в дерево конструирования FeatureManager. Когда вы перетаскиваете дерево вверх или вниз, каждый элемент, который вы перетаскиваете, выделяется. Имя объекта, который вы перемещаете, падает сразу под выделенным в данный момент элементом, когда вы отпускаете указатель.

Что такое функция в SOLIDWORKS?

Элементы — это отдельные формы, которые при объединении составляют деталь. Вы также можете добавлять в сборки некоторые типы элементов. Особенности включают возможность работы с многотельными деталями. Вы можете включать отдельные элементы выдавливания, вращения, лофта или развертки в один и тот же документ детали.

Как отобразить элементы в SOLIDWORKS?

Чтобы отобразить описания элементов: В верхней части дерева конструирования FeatureManager щелкните правой кнопкой мыши имя детали, сборки или чертежа и выберите Отображение дерева > Показать описания элементов. По умолчанию описания функций совпадают с именами функций и не отображаются.

Что такое таблица параметров SOLIDWORKS?

Таблица параметров позволяет создавать несколько конфигураций деталей или сборок, указывая параметры во встроенном листе Microsoft Excel. Таблица параметров сохраняется в документе модели и не связана с исходным файлом Excel.

Какова цель дерева конструирования Feature Manager при рисовании с помощью SOLIDWORKS?

все они доступны на панели менеджера SOLIDWORKS, известной как дерево проектирования Feature Manager. Он позволяет выбирать элементы в модели по имени, скрывать и восстанавливать элементы деталей и компонентов сборки, переименовывать элементы, просматривать родительские/дочерние элементы элемента и многое другое.

Что означает (-) в SOLIDWORKS?

тому назад. Дополнительные действия с комментариями. (-) означает, что он не полностью ограничен/определен.

Как отобразить диспетчер функций в SOLIDWORKS?

Вы можете включить характеристики отображения дерева конструирования FeatureManager, выбрав параметры в подменю Отображение дерева контекстного меню FeatureManager. Чтобы получить доступ к этим параметрам, щелкните правой кнопкой мыши имя сборки в дереве конструирования FeatureManager и выберите Отображение дерева.

Что такое домик на дереве SOLIDWORKS?

SOLIDWORKS Treehouse — это отдельное приложение, предназначенное для создания сборочных структур и управления ими еще до начала моделирования в SOLIDWORKS.

Как изменить имя элемента в SOLIDWORKS?

Переименование компонентов в дереве конструирования FeatureManager

1. Щелчок-пауза-щелчок по компоненту.
2. Щелкните компонент правой кнопкой мыши и выберите «Переименовать сборку» или «Переименовать деталь».
3. Выберите компонент и нажмите F2.

Как показать дерево сборки в SOLIDWORKS?

Щелкните правой кнопкой мыши деталь или сборку верхнего уровня в дереве элементов. Выберите опцию «Отображение дерева» в меню. Выберите параметры, которые лучше всего подходят для того, как вы хотите, чтобы дерево выглядело.

Источник

Структура данных B-дерево

Всем привет! Мы запустили новый набор на курс «Алгоритмы для разработчиков» и сегодня хотим поделиться интересным переводом, подготовленным для студентов данного курса.

В деревьях поиска, таких как двоичное дерево поиска, AVL дерево, красно-чёрное дерево и т.п. каждый узел содержит только одно значение (ключ) и максимум двое потомков. Однако есть особый тип дерева поиска, который называется B-дерево (произносится как Би-дерево). В нем узел содержит более одного значения (ключа) и более двух потомков. B-дерево было разработано в 1972 году Байером и МакКрейтом и называлось Сбалансированное по высоте дерево поиска порядка m (Height Balanced m-way Search Tree). Свое современное название B-дерево получило позже.

B-дерево можно определить следующим образом:
B-дерево – это сбалансированное дерево поиска, в котором каждый узел содержит множество ключей и имеет более двух потомков.

Здесь количество ключей в узле и количество его потомков зависит от порядка B-дерева. Каждое B-дерево имеет порядок.

B-дерево порядка m обладает следующими свойствами:

Свойство 1: Глубина всех листьев одинакова.
Свойство 2: Все узлы, кроме корня должны иметь как минимум (m/2) – 1 ключей и максимум m-1 ключей.
Свойство 3: Все узлы без листьев, кроме корня (т.е. все внутренние узлы), должны иметь минимум m/2 потомков.
Свойство 4: Если корень – это узел не содержащий листьев, он должен иметь минимум 2 потомка.
Свойство 5:Узел без листьев с n-1 ключами должен иметь n потомков.
Свойство 6: Все ключи в узле должны располагаться в порядке возрастания их значений.

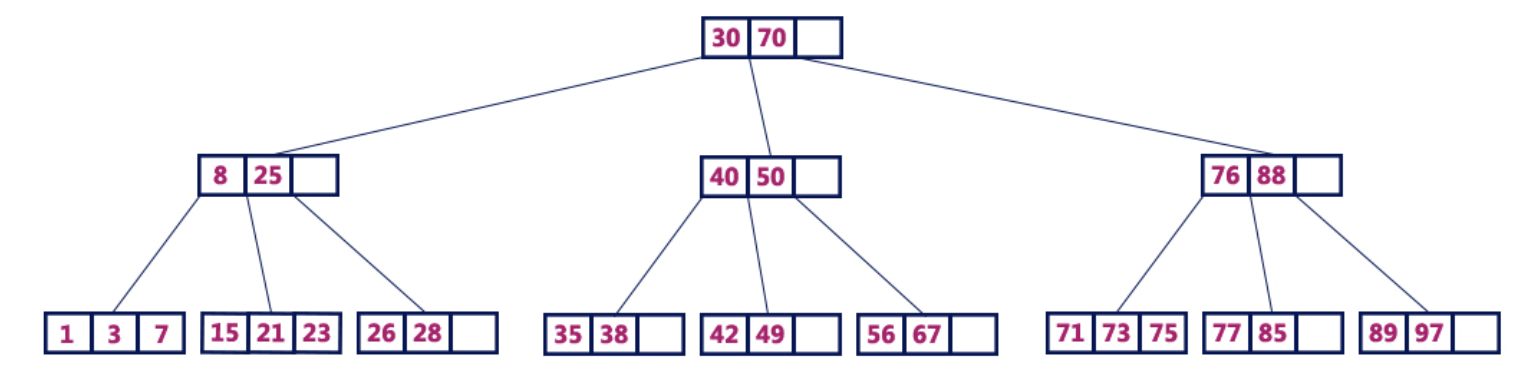
Например, B-дерево 4 порядка содержит максимум 3 значения ключа и максимум 4 потомка для каждого узла.

B-дерево 4 порядка

Операции над B-деревом

Поиск по B-дереву аналогичен поиску по двоичному дереву поиска. В двоичном дереве поиска поиск начинается с корня и каждый раз принимается двустороннее решение (пойти по левому поддереву или по правому). В В-дереве поиск также начинается с корневого узла, но на каждом шаге принимается n-стороннее решение, где n – это общее количество потомков рассматриваемого узла. В В-дереве сложность поиска составляет O(log n). Поиск происходит следующим образом:

Шаг 1: Считать элемент для поиска.
Шаг 2: Сравнить искомый элемент с первым значением ключа в корневом узле дерева.
Шаг 3: Если они совпадают, вывести: «Искомый узел найден!» и завершить поиск.
Шаг 4: Если они не совпадают, проверить больше или меньше значение элемента, чем текущее значение ключа.
Шаг 5: Если искомый элемент меньше, продолжить поиск по левому поддереву.
Шаг 6: Если искомый элемент больше, сравнить элемент со следующим значением ключа в узле и повторять Шаги 3, 4, 5 и 6 пока не будет найдено совпадение или пока искомый элемент не будет сравнен с последним значением ключа в узле-листе.
Шаг 7: Если последнее значение ключа в узле-листе не совпало с искомым, вывести «Элемент не найден!» и завершить поиск.

Операция вставки в B-дерево

В В-дереве новый элемент может быть добавлен только в узел-лист. Это значит, что новая пара ключ-значение всегда добавляется только к узлу-листу. Вставка происходит следующим образом:

Шаг 1: Проверить пустое ли дерево.
Шаг 2: Если дерево пустое, создать новый узел с новым значением ключа и его принять за корневой узел.
Шаг 3: Если дерево не пустое, найти подходящий узел-лист, к которому будет добавлено новое значение, используя логику дерева двоичного поиска.
Шаг 4: Если в текущем узле-листе есть незанятая ячейка, добавить новый ключ-значение к текущему узлу-листу, следуя возрастающему порядку значений ключей внутри узла.
Шаг 5: Если текущий узел полон и не имеет свободных ячеек, разделите узел-лист, отправив среднее значение родительскому узлу. Повторяйте шаг, пока отправляемое значение не будет зафиксировано в узле.
Шаг 6: Если разделение происходит с корнем дерева, тогда среднее значение становится новым корнем дерева и высота дерева увеличивается на единицу.

Давайте создадим B-дерево порядка 3, добавляя в него числа от 1 до 10.

Insert(1):
Поскольку «1» — это первый элемент дерева – он вставляется в новый узел и этот узел становится корнем дерева.

Insert(2):
Элемент «2» добавляется к существующему узлу-листу. Сейчас у нас всего один узел, следовательно он является и корнем и листом одновременно. В этом листе имеется пустая ячейка. Тогда «2» встает в эту пустую ячейку.

Insert(3):
Элемент «3» добавляется к существующему узлу-листу. Сейчас у нас только один узел, который одновременно является и корнем и листом. У этого листа нет пустой ячейки. Поэтому мы разделяем этот узел, отправляя среднее значение (2) в родительский узел. Однако у текущего узла родительского узла нет. Поэтому среднее значение становится корневым узлом дерева.

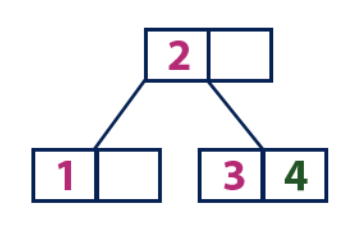
Insert(4):
Элемент «4» больше корневого узла со значением «2», при этом корневой узел не является листом. Поэтому мы двигаемся по правому поддереву от «2». Мы приходим к узлу-листу со значением «3», у которого имеется пустая ячейка. Таким образом, мы можем вставить элемент «4» в эту пустую ячейку.

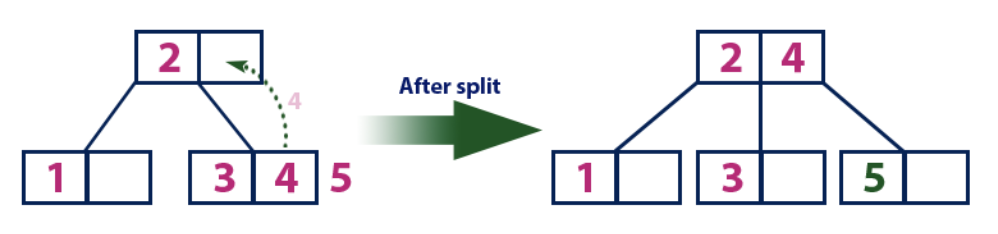
Insert(5):
Элемент «5» больше корневого узла со значением «2», при этом корневой узел не является листом. Поэтому мы двигаемся по правому поддереву от «2». Мы приходим к узлу-листу и обнаруживаем, что он уже полон и не имеет пустых ячеек. Тогда мы делим этот узел, отправляя среднее значение (4) в родительский узел (2). В родительском узле есть для него пустая ячейка, поэтому значение «4» добавляется к узлу, в котором уже есть значение «2», а новый элемент «5» добавляется в качестве нового листа.

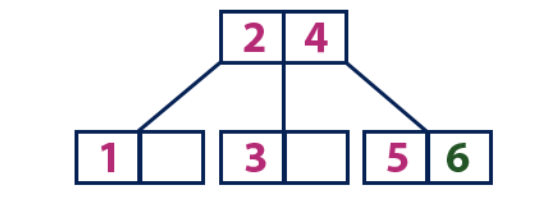
Insert(6):
Элемент «6» больше, чем элементы корня «2» и «4», который не является листом. Мы двигаемся по правому поддереву от элемента «4». Мы достигаем листа со значением «5», у которого есть пустая ячейка, поэтому элемент «6» помещаем как раз в нее.

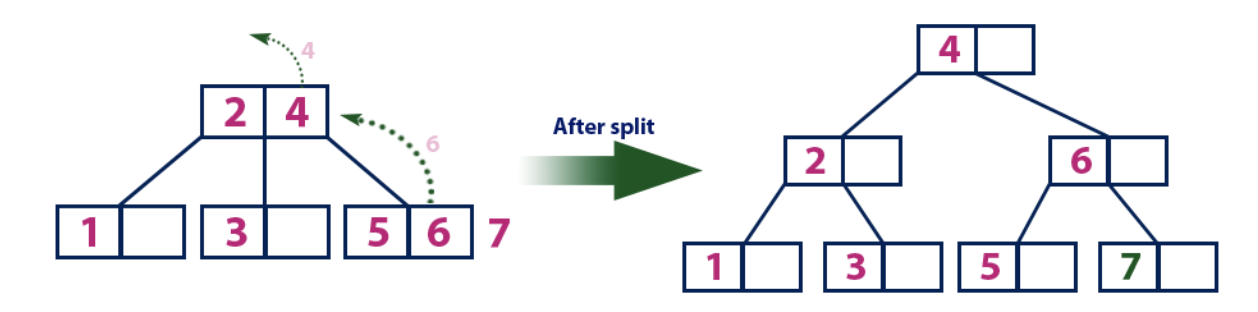
Insert(7):
Элемент «7» больше, чем элементы корня «2» и «4», который не является листом. Мы двигаемся по правому поддереву от элемента «4». Мы достигаем узла-листа и видим, что он полон. Мы делим этот узел, отправляя среднее значение «6» вверх к родительскому узлу с элементами «2» и «4». Однако родительский узел тоже полон, поэтому мы делим узел с элементами «2» и «4», отправляя значение «4» родительскому узлу. Только вот этого узла еще нет. В таком случае узел с элементом «4» становится новым корнем дерева.

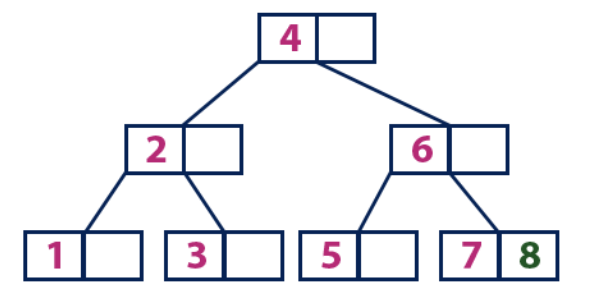
Insert(8):
Элемент «8» больше корневого узла со значением «4», при этом корневой узел не является листом. Мы двигаемся по правому поддереву от элемента «4» и приходим к узлу со значением «6». «8» больше «6» и узел с элементом «6» не является листом, поэтому двигаемся по правому поддереву от «6». Мы достигаем узла-листа с «7», у которого есть пустая ячейка, поэтому в нее мы помещаем «8».

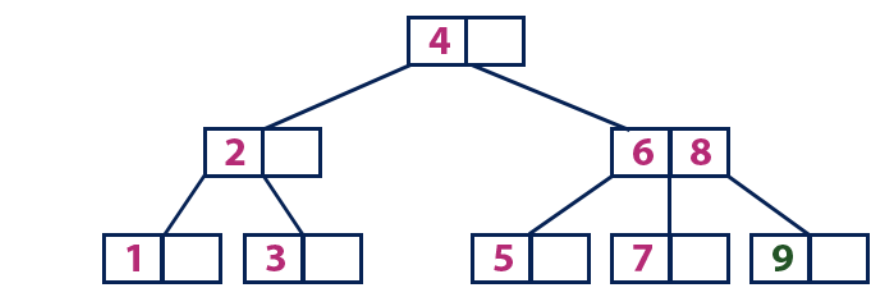
Insert(9):
Элемент «9» больше корневого узла со значением «4», при этом корневой узел не является листом. Мы двигаемся по правому поддереву от элемента «4» и приходим к узлу со значением «6». «9» больше «6» и узел с элементом «6» не является листом, поэтому двигаемся по правому поддереву от «6». Мы достигаем узла-листа со значениями «7» и «8». Он полон. Мы делим этот узел, отправляя среднее значение (8) родительскому узлу. Родительский узел «6» имеет пустую ячейку, поэтому мы помещаем «8» в нее. При этом новый элемент «9» добавляется в узел-лист.

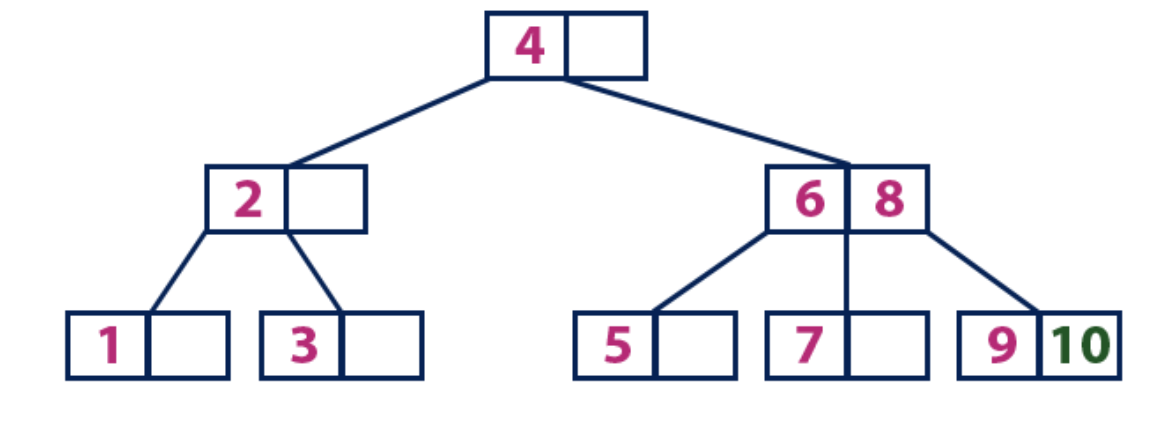
Insert(10):
Элемент «10» больше корневого узла со значением «4», при этом корневой узел не является листом. Мы двигаемся по правому поддереву от элемента «4» и приходим к узлу со значениями «6» и «8». «10» больше «6» и «8» и узел с этими элементами не является листом, поэтому двигаемся по правому поддереву от «8». Мы достигаем узла-листа со значением «9». У него есть пустая ячейка, поэтому туда мы помещаем «10».

Предлагаем вам самостоятельно на практике понять, как устроены В-деревья, воспользовавшись этой визуализацией.

Ждем всех на бесплатном открытом уроке, который пройдет уже 12 июля. До встречи!

Источник