Неоднозначность в контекстно-свободных грамматиках
Аннотация: В данной лекции рассматривается класс контекстно-свободных языков, которые находят применение в разнообразных программных продуктах, таких как компиляторы, средства форматирования исходного кода, средства статического анализа программ, синтаксические редакторы, системы верстки, программы просмотра форматированного текста, поисковые системы. Приведены практические примеры и упражнения для самостоятельного решения
Перейдем к более богатому классу языков — к контекстно-свободным языкам. Они находят применение в разнообразных программных продуктах, таких как компиляторы, средства форматирования исходного кода, средства статического анализа программ, синтаксические редакторы, системы верстки, программы просмотра форматированного текста, поисковые системы.
Начнем рассмотрение контекстно-свободных языков с введения понятия деревьев вывода, что позволит определить важное для компьютерных приложений понятие однозначности контекстно-свободной грамматики. Чтобы не вдаваться в детали определения изоморфизма ориентированных деревьев , будем использовать в определении однозначности понятие левостороннего вывода (раздел 7.2). Соответствие деревьев вывода и левосторонних (а также правосторонних) выводов понадобится также в «лекции 13» .
Из класса всех контекстно-свободных языков можно выделить подкласс тех языков, для которых существует хотя бы одна однозначная грамматика . В разделе 7.3* доказывается, что все праволинейные (то есть автоматные) языки принадлежат этому подклассу.
В последнем разделе этой лекции приводятся важные конкретные примеры однозначных контекстно-свободных грамматик, моделирующих системы правильно вложенных скобок и польскую (префиксную) запись выражений.
7.1. Деревья вывода
Определение 7.1.1. Выводам в контекстно-свободной грамматике соответствуют так называемые деревья вывода ( деревья разбора, derivation tree , parse tree ) — некоторые упорядоченные деревья, вершины которых помечены символами алфавита . Корень дерева отвечает начальному символу. Каждому символу слова w1 , на которое заменяется начальный символ на первом шаге вывода, ставится в соответствие вершина дерева, и к ней проводится дуга из корня. Полученные таким образом непосредственные потомки корня упорядочены согласно порядку их меток в слове w1 . Для тех из полученных вершин, которые помечены символами из множества N , делается аналогичное построение, и т. д.
Кроной ( yield ) дерева вывода называется слово, записанное в вершинах, помеченных символами из алфавита .
Пример 7.1.2. Рассмотрим контекстно-свободную грамматику
Упражнение 7.1.4. Существует ли праволинейная грамматика без -правил, в которой некоторое слово имеет бесконечно много выводов?
Источник
Построение деревьев разбора контекстно-свободных грамматик. Контекстно-свободные грамматики

Язык — это множество строк, которые могут быть сгенерированы некоторым деревом разбора. Процесс поиска дерева разбора для данной строки терминалов называется разбором или синтаксическим анализом этой строки.
Пример 3. Вывод 9-5+2 в грамматике примера 1 показан деревом:
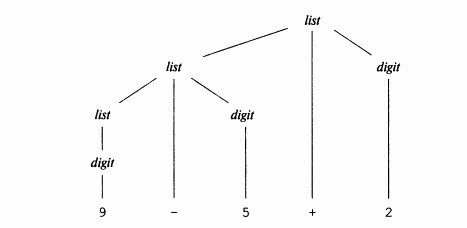
Рис. Дерево разбора строки 9-5+2 в соответствии с грамматикой примера 1.
list list + digit — продукция грамматики примера 1. Левый дочерний узел корня аналогичен корню, только его дочерний узел помечен как – вместо +, все узлы, помеченные как digit имеют по одному дочернему узлу с метками-цифрами. Листьями является строка 9-5+2
Пример 4. Синтаксические деревья позволяют моделировать синтаксические структуры предложений естественного языка:
§ Для каждого синтаксического дерева существует, по крайней мере, один вывод.
§ Для каждого вывода есть соответствующее синтаксическое дерево (но несколько выводов могут иметь одно и то же дерево).
§ Каждый узел дерева помечен символом грамматики. Каждый внутренний узел и его дочерние узлы соответствуют продукции: внутренний узел соответствует заголовку продукции, а дочерни узлы — телу продукции.
§ Концевые узлы дерева образуют выводимую сентенциальную форму.
3. Неоднозначность грамматики
Грамматика может иметь более одного дерева разбора для данной строки терминалов.
Такая грамматика называется неоднозначной.
КС-грамматика G называется неоднозначной, если существует хотя бы одна цепочка L (G), для которой может быть построено два или более различных деревьев вывода.
Это утверждение эквивалентно тому, что цепочка имеет два или более разных левосторонних (или правосторонних) вывода.
В противном случае грамматика называется однозначной.
Язык, порождаемый грамматикой, называется неоднозначным, если он не может быть порожден никакой однозначной грамматикой.
Чтобы показать неоднозначность грамматики, достаточно найти строку терминалов, которая дает более одного дерева разбора.
Неоднозначность грамматики — это свойство грамматики, а не языка. Т.е. для некоторых неоднозначных грамматик существует эквивалентные им однозначные грамматики.
Если грамматика используется для определения языка программирования, то она должна быть однозначной.
В этой грамматике для цепочки if then if then a else a можно построить два различных вывода.
Разные деревья вывода предполагают соответствие else разным then. Если договориться, что else должно соответствовать ближайшему к нему then, и подправить грамматику G, то неоднозначность будет устранена:
S if b then S| if b then S’ else S | a
S’ if b then S’ else S’| a
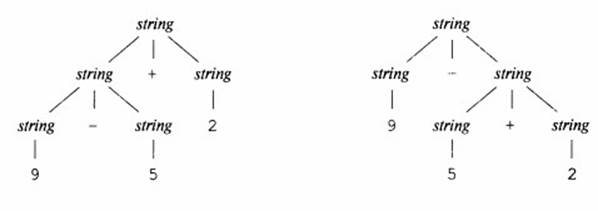
Пример 6 Если в примере 1 использовать только один нетерминал string, то грамматику можно записать: string string + string | string – string|0|1|2|3|4|5|6|7|8|9
Объединение записей для digit и list имеет кажущийся смысл, т.к. отдельная цифра является частным случаем списка. Но при этом, например, для выражения 9-5+2, в такой грамматике существует больше одного дерева разбора Эти два дерева разбора соответствуют двум вариантам расстановки скобок в выражении: (9-5)+2 и 9-(5+2). Второе выражение дает в результате значение 2 вместо 6. Грамматика примера 1 не допускает такой интерпретации.
Дерево вывода можно строить нисходящим либо восходящим способом.
При нисходящем разборе дерево вывода формируется от корня к листьям; на каждом шаге для вершины, помеченной нетерминальным символом, пытаются найти такое правило вывода, чтобы имеющиеся в нем терминальные символы «проектировались» на символы исходной цепочки.
Метод восходящего разбора заключается в том, чтобы исходную цепочку сворачивают к начальному символу S; на каждом шаге ищется подцепочка, которая совпадает с правой частью какого –либо правила вывода; если такая подцепочка находится, то она заменяется нетерминалом из левой части этого правила.
Если грамматика однозначная, то при любом способе построения будет получено одно и то же дерево разбора.
5. Ассоциативность операторов
По соглашению 9+5+2 эквивалентно (9+5)+2, а 9-5-2 эквивалентно (9-5)-2. Когда операнд типа 5 имеет операторы и слева, и справа, необходимы
Похожие материалы
Источник
3.10. Контекстно-свободные языки
Из четырёх классов грамматики иерархии Хомского класс контекстно-свободных языков наиболее важен с точки зрения приложения к языкам программирования и компиляции. С их помощью можно определить большую часть синтаксических структур языков программирования. Кроме того, они служат основой различных схем перевода, т.к. в ходе процесса компиляции синтаксическую структуру, передаваемую входной программе КС-грамматикой, можно использовать при построении перевода этой программы.
Синтаксическую структуру входной цепочки можно определить по последовательности правил, применяемых при выводе этой цепочки. Таким образом, на часть компилятора, называемую синтаксическим анализатором, можно смотреть как на устройство, которое пытается выяснить, существует ли в некоторой фиксированной КС-грамматике вывод входной цепочки.
Естественно, что эта задача нетривиальная – по данной КС-грамматике G и входной цепочке w выяснить, принадлежит ли w языку L(G), и если «да», то найти вывод цепочки w в грамматике G.
3.10.1. Деревья выводов
В грамматике может быть несколько выводов, эквивалентных в том смысле, что во всех них применяются одни и те же правила в одних и тех же местах, но в различном порядке. КС-грамматика позволяет ввести удобное графическое представление класса эквивалентных выводов, называемое деревом выводов.
Дерево вывода в КС-грамматике G = (N, Р S),
где N – конечное множество нетерминальных символов;
— непересекающееся с N множество терминальных символов;
Р – конечное подмножество множества (N) N(N) (N) (элемент ( ) множества Р называется правилом или продукцией );
S – выделенный символ из N, называемый начальным или исходным символом,
— это помеченное упорядоченное дерево, каждая вершина которого помечена символом из множества Ne>.
Если внутренняя вершина помечена символом А, а её прямые потомки — символами 

Помеченное упорядоченное дерево D называется деревом вывода (или деревом разбора) в КС-грамматике G(А) = (N, Р A), если выполняются следующие условия:
если 

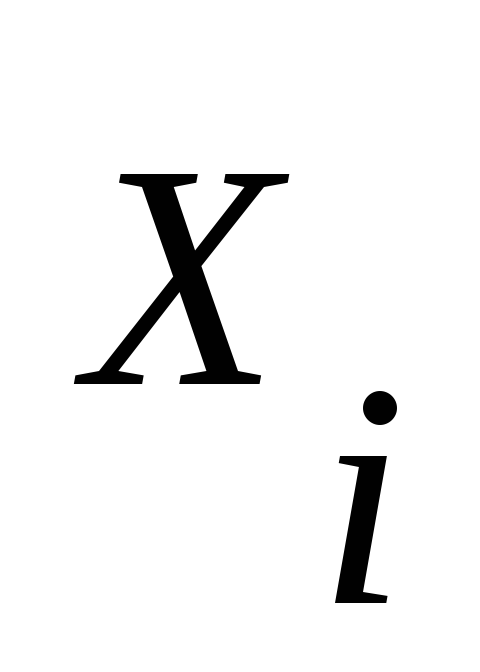








Пример. Имеем грамматику G=G(S) с правилами SaSbS | bSaS | e (рис.3.7).

Рис. 3.7. Деревья выводов

SaSbS | bSaS | e
Заметим, что существует единственное упорядочение вершин упорядоченного дерева, у которого прямые потомки вершины упорядочиваются «слева направо».
Допустим, что n – вершина и 
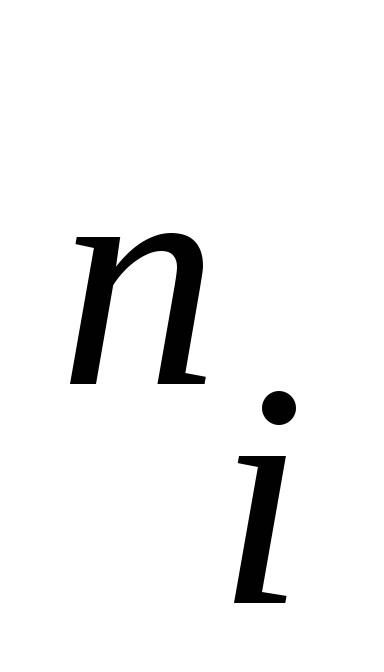
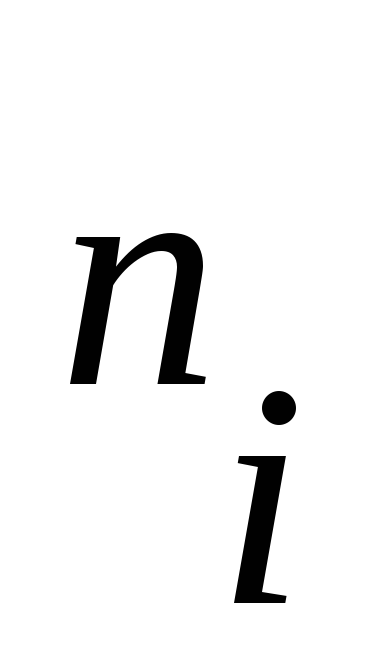
Кроной дерева вывода назовём цепочку, которая получится, если выписать слева направо метки листьев.
Кроны наших деревьев: S, е, abab, abab.
Сечением дерева D назовём такое множество С вершин дерева D, что
никакие две вершины из С не лежат на одном пути в D;
ни одну вершину дерева D нельзя добавить к С, не нарушив свойства 1).
Множество вершин дерева, состоящего из одного корня, является сечением.
Листья также образуют сечение.

Рис. 3.8. Пример сечения дерева
Кроной сечения дерева D является цепочка, получаемая конкатенацией (в порядке слева направо) меток вершин, образующих некоторое сечение.
Крона сечения примера, приведенного на рис.3.7, — abaSbS.
Пусть S= 



Пусть D – дерево вывода в КС-грамматике G = (N, Р S) с кроной . Тогда S (транзитивное и рефлексивное замыкание , т.е. выводима из S).

Пусть – такая последовательность сечений дерева D, что
С0 – содержит только один корень дерева D;



– крона дерева D.
Ясно, что хотя бы одна такая последовательность существует.
Если 
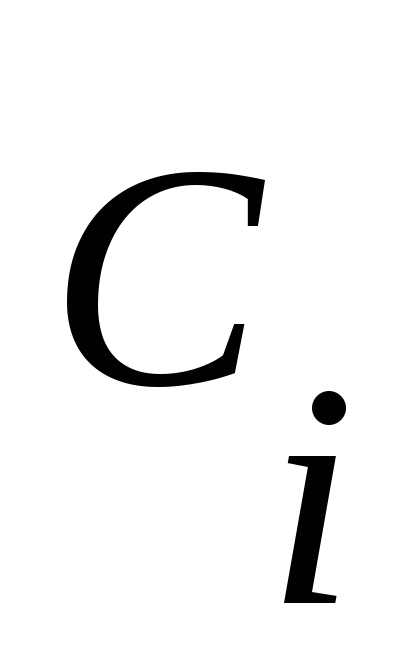


Если S= 





Каждая следующая цепочка 


Пример. Рассмотрим КС-грамматику G0 с правилами
Нарисуем дерево вывода (рис 3.7).

Рис. 3.9. Пример дерева вывода
Это дерево служит представлением десяти эквивалентных выводов цепочки а+а.
Е Е+Т Т+Т F+Т а+Т а+Fа+а – левый вывод.
Е Е+Т Е+F Е+а Т+а F+аа+а – правый вывод.
Определение. Цепочку будем называть левовыводимой, если существует левый вывод S= 



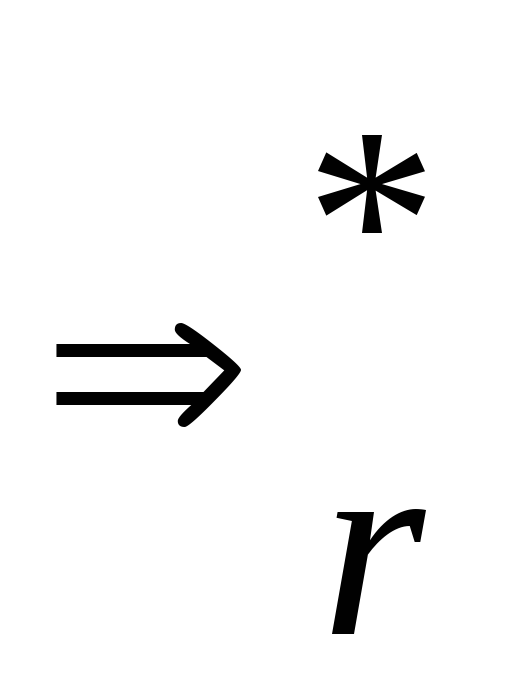



Источник

