Контрольная метод деревьев решений

Применение метода анализа данных — деревья решений

Разработка и принятие правильного решения как задачи работы управленческого персонала организации. Деревья решений — один из методов автоматического анализа данных, преимущества их использования и область применения. Построение деревьев классификации.

Подобные документы

Изучение методов моделирования и анализа панельных данных. Построение ABC-XYZ классификации среди данных широкой номенклатуры по товарным запасам торгового предприятия. Виды исходных данных и построение на их основе модели регрессии по панельным данным.

Повышение обоснованности принимаемого решения, анализ вариантов как цель системного анализа, его применение на примере обустройства детской комнаты. Построение дерева целей, расчет коэффициентов относительной важности. Деревья мероприятий, сетевой график.

Математическая модель задачи принятия решения в условиях риска. Нахождение оптимального решения по паре критериев. Построение реализационной структуры задачи принятия решения. Ориентация на математическое ожидание, среднеквадратичное отклонение.

Классификационные принципы методов прогнозирования: фактографические, комбинированные и экспертные. Разработка приёмов статистического наблюдения и анализа данных. Практическое применение методов прогнозирования на примере метода наименьших квадратов.

Разработка и исследование эконометрических методов с учетом специфики экономических данных и в соответствии с потребностями экономической науки и практики. Применение эконометрических методов и моделей для статистического анализа экономических данных.

Дисперсионный анализ — исследование причин отклонений фактических затрат от нормативных. Схемы организации исходных данных с двумя и более факторами. Формулы расчета межгрупповой и внутригрупповой дисперсии. Задачи двухфакторного дисперсионного анализа.

Задачи оптимизации сложных систем и подходы к их решению. Программная реализация анализа сравнительной эффективности метода изменяющихся вероятностей и генетического алгоритма с бинарным представлением решений. Метод решения задачи символьной регрессии.

Построение модели планирования производства. Использование инструментального средства «Поиск решения» для решения задачи линейного программирования. Решение оптимальной задачи, с использованием методов математического анализа и возможностей MathCad.

Построение графического дерева решений по установленному критерию оптимальности. Анализ узлов дерева решений с точки зрения доступности информации. Определение вектора приоритетов альтернатив, используя метод анализа иерархий и матрицы парных сравнений.

Математическая формулировка экономико-математической задачи. Вербальная постановка и разработка задачи о составлении графика персонала. Решение задачи о составлении графика персонала с помощью программы Microsoft Excel. Выработка управленческого решения.

Источник

1. Дерево решений

Своевременная разработка и принятие правильного решения — главные задачи работы управленческого персонала любой организации. Непродуманное решение может дорого стоить компании. На практике результат одного решения заставляет нас принимать следующее решение и т. д. Когда нужно принять несколько решений в условиях неопределенности, когда каждое решение зависит от исхода предыдущего или исходов испытаний, то применяют схему, называемую деревом решений.

Дерево решений — это графическое изображение процесса принятия решений, в котором отражены альтернативные решения, альтернативные состояния среды, соответствующие вероятности и выигрыши для любых комбинаций альтернатив и состояний среды.

Рисуют деревья слева направо. Места, где принимаются решения, обозначают квадратами □, места появления исходов — кругами О,

возможные решения — пунктирными линиями—-, возможные исходы — сплошными линиями—-.

Задачи с решениями

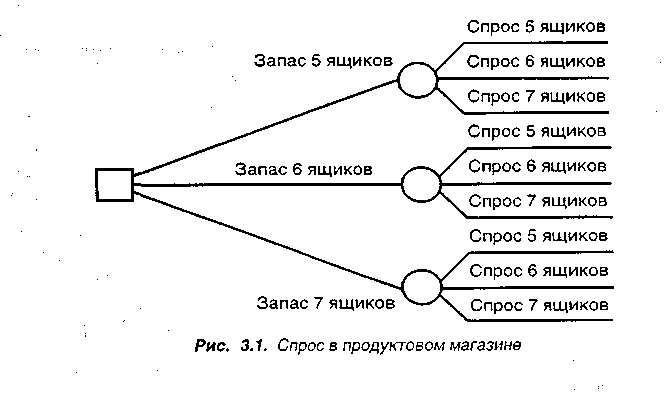
З адача 3.1 Ежедневный спрос на ящики с напитком в продуктовом магазине может быть пять, шесть или семь ящиков. Покажем дерево решений, которое иллюстрирует альтернативы запасов пяти, шести или семи ящиков.

Решение Дерево решений показано на рис. 3.1.

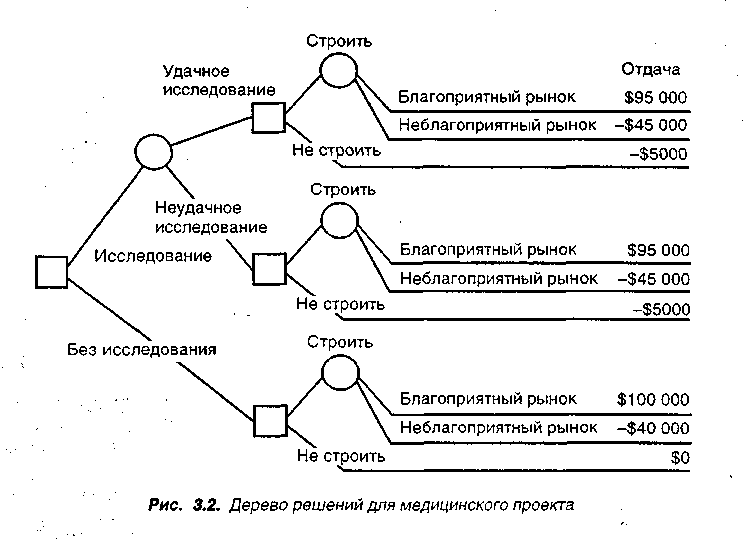
З адача 3.2 Группа медиков собирается открыть частную медицинскую фирму. Если рынок будет благоприятным, они будут иметь прибыль $100000. Если рынок неблагоприятный, они понесут потери $40000. Они также могут осуществить маркетинговое исследование, которое стоит $5000. Результаты исследования могут быть благоприятными или неблагоприятными. Медики хотят построить дерево решений и отразить на нем свою денежную отдачу. Дерево решений показано на рис. 3.2.

Решение В определении денежной отдачи для каждой ветви необходимо вычесть $5000 для тех ветвей дерева, где исследования проводились, т. е. для шести ветвей.

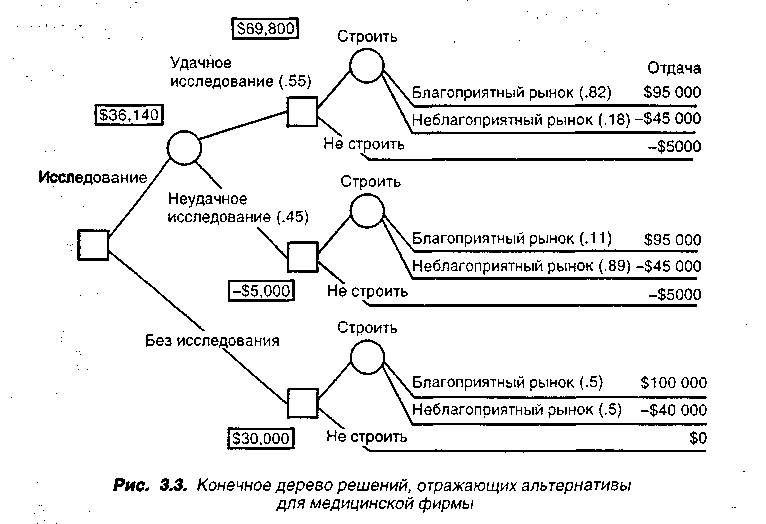
Далее, когда отдача определена для каждого исхода, или ветви дерева решений, следующий шаг состоит в установлении вероятностей каждого состояния внешней среды (см. рис. 3.3). Такие вероятности должен определить менеджер, принимающий решение на рынке. Тогда мы можем анализировать полностью дерево решений.

И з решения, отраженного на рис. 3.3, очевидно, что группа исследования рынка приглашается. Если исследование благоприятное, клиника должна быть построена, если нет, то клинику строить не будут. Решение с участием маркетинговой группы дает отдачу $36140, а без участия исследователей и при строительстве клиники приносит $30000. Тогда лучшее решение – проводить исследование и принимать решение на основе полученных рекомендаций.

Задача 3.3. Для каждой альтернативы мы считаем ожидаемую стоимостную оценку (EMV) — максимальную из сумм оценок выигрышей, умноженных на вероятность реализации выигрышей, для всех возможных вариантов.

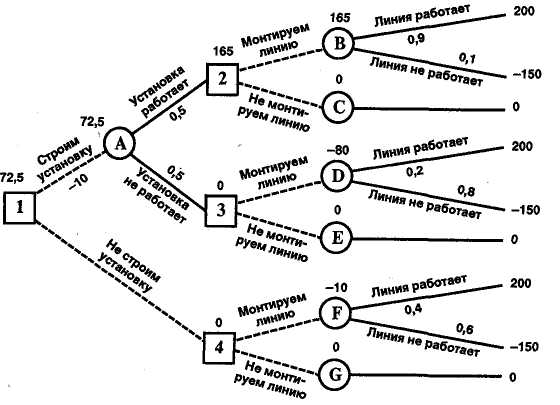
Главному инженеру компании надо решить, монтировать или нет новую производственную линию, использующую новейшую технологию. Если новая линия будет работать безотказно, компания получит прибыль 200 млн. рублей. Если же она откажет, компания может потерять 150 млн. рублей. По оценкам главного инженера, существует 60% шансов, что новая производственная линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет производственную линию. Эксперимент обойдется в 10 млн. рублей. Главный инженер считает, что существует 50% шансов, что экспериментальная установка будет работать. Если экспериментальная установка будет работать, то 90% шансов за то, что смонтированная производственная линия также будет работать. Если же экспериментальная установка не будет работать, то только 20% шансов за то, что производственная линия заработает. Следует ли строить экспериментальную установку? Следует ли монтировать производственную линию? Какова ожидаемая стоимостная оценка наилучшего решения?

В узле F возможны исходы «линия работает» с вероятностью 0,4 (что приносит прибыль 200) и «линия не работает» с вероятностью 0,6 (что приносит убыток -150) => оценка узла F: EMV(F) = 0,4X200 + 0,6х(-150) = -10. Это число мы пишем над узлом F.

В узле 4 мы выбираем между решением «монтируем линию» (оценка этого решения EMV(F) = -10) и решением «не монтируем линию» (оценка этого решения EMV((G) = 0): EMV(4) = max = max = 0 = EMV(G). Эту оценку мы пишем над узлом 4, а решение «монтируем линию» отбрасываем и зачеркиваем.

EMV(B) = 0,9*200 + 0,1*(-150) = 180 — 15 = 165

EMV(2) = max = max = 165 = EMV(B). Поэтому в узле 2 отбрасываем возможное решение «не монтируем линию».

EMV(.D) = 0,2*200 + 0,8*(-150) = 40 — 120 = -80.

E MV(E) = 0.

EMV(3) = max = max = 0 = EMV(E). Поэтому в узле 3 отбрасываем возможное решение «монтируем линию».

EMV(A) = 0,5*165 + 0,5*0 — 10 = 72,5.

Поэтому в узле 1 отбрасываем возможное решение «не строим установку».

Ожидаемая стоимостная оценка наилучшего решения равна 72,5 млн. рублей. Строим установку. Если установка работает, то монтируем линию. Если установка не работает, то линию монтировать не надо.

Источник