Красно черные деревья удаление элемента

Удаление узлов из красно-чёрного дерева

Удаление узлов из красно-чёрного дерева — непростая задача, поэтому имеет смысл разделить её на несколько частей и рассмотреть каждый случай отдельно.

Использовано изображение портала cartoonbank.ru

В прошлой статье мы рассмотрели правила формирования красно-чёрного дерева поиска и рассмотрели случаи балансировки при добавлении элементов.

Теперь поговорим об удалении элементов.

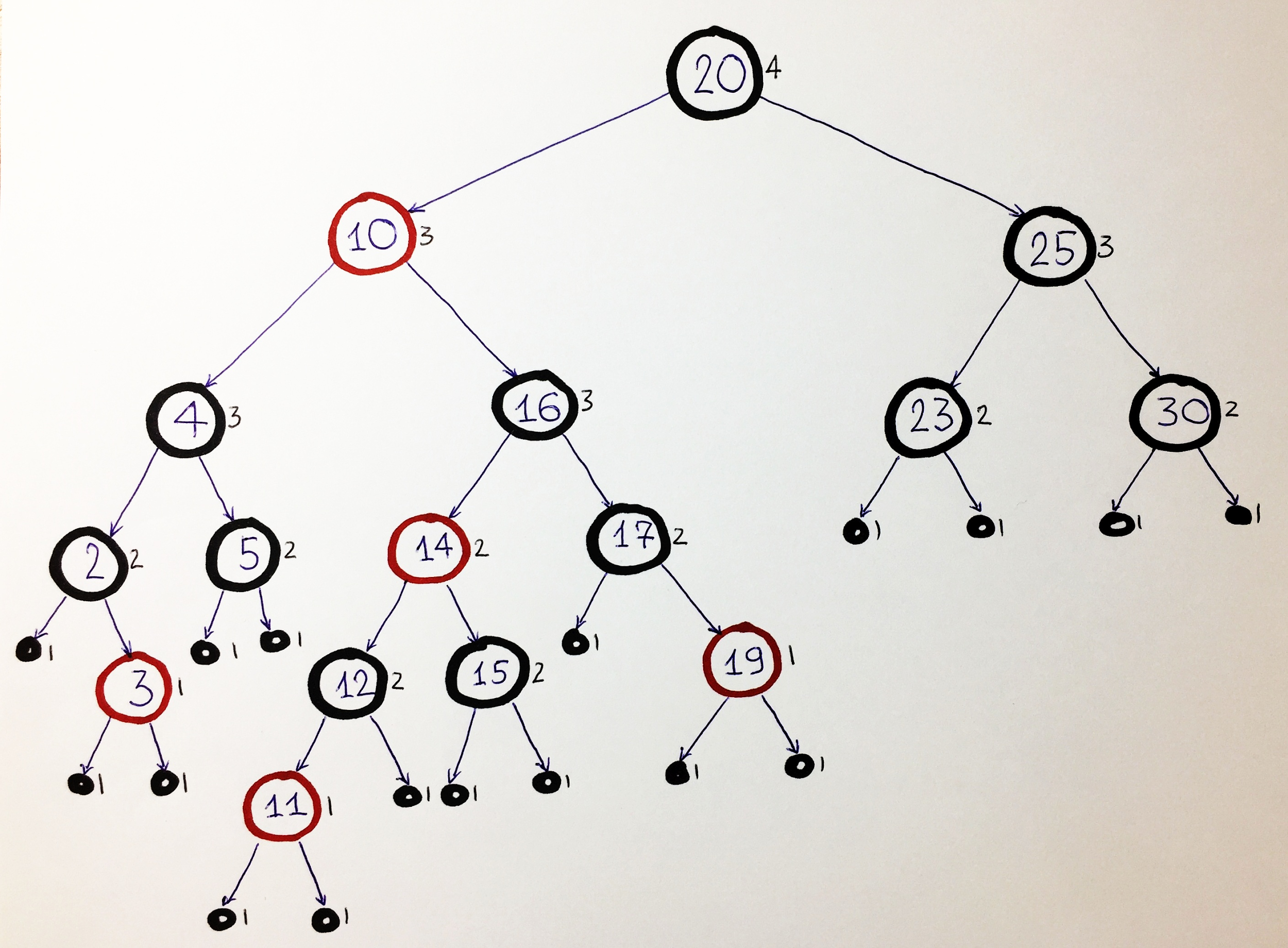
Возьмём, для примера, вот такое красно-чёрное дерево:

Напомним, что главное свойство красно-чёрного дерева — одинаковая чёрная высота слева и справа от каждого узла. Поэтому на рисунках рядом с каждым узлом мы будем указывать значение чёрной высоты, чтобы на каждом этапе мы могли проверять её стабильность.

Разделяй и властвуй

Удаление элемента из красно-чёрного дерева — не такая простая задача, как может показаться на первый взгляд, поэтому предлагаю разделить её на несколько частей и рассмотреть каждую в отдельности.

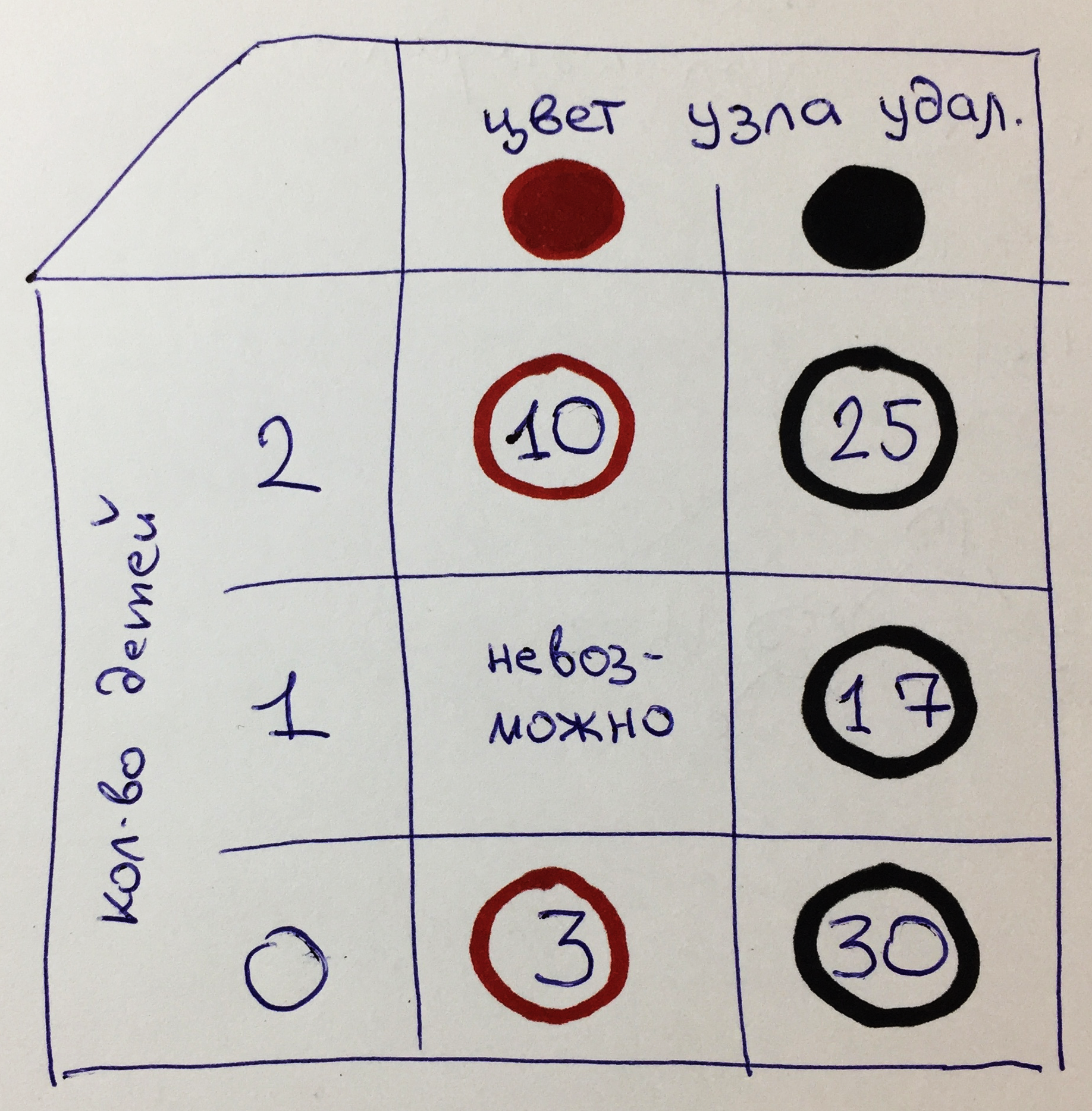
Сначала разделим задачу по двум категориям:

• цвет удаляемого узла: К или Ч
• количество дочерних узлов: 2, 1 или 0

В результате у нас получится матрица из 6 вариантов: К2, Ч2, К1, Ч1, К0, Ч0.
Для каждого варианта указан соответствующий узел нашего дерева.
Рассмотрим процесс удаления для каждого варианта.

К2 — красный узел с двумя детьми

Задача удаления узла с двумя дочерними элементами сводится к задаче удаления узла с одним или нулём дочерних элементов.

Для этого необходимо найти ближайший элемент, который меньше или больше удаляемого и поменять их местами.

Обратите внимание, что при обмене элементов местами нужно изменять только значения в узлах, а цвет оставлять прежним, чтобы не нарушать структуру дерева и не изменять чёрную высоту.
После обмена нужно удалить элемент из его нового места. Это будет либо самый правый элемент в левой ветке (максимальный слева), либо самый левый в правой (минимальный справа), в любом случае у него не будет одного ребёнка слева или справа. Таким образом, задача удаления узла с 2 детьми сводится к задаче удаления элемента с 1 или 0 детьми:

Ч2 — чёрный узел с двумя детьми

Аналогично предыдущему случаю, приведём пример удаления чёрного узла 16.

Как видим, после обмена задача сводится к удалению элемента с одним ребёнком:

К1 — красный узел с одним ребёнком

Если у красного узла одного ребёнка нет, значит, вместо него находится чёрный NIL-элемент и чёрная высота красного узла равна 1. Следовательно, с другой стороны чёрная высота также должны быть равна 1. Но так как у красного узла дочерний элемент не может быть красного цвета, то другой его ребёнок должен быть чёрного цвета. Так как чёрная высота должна быть равна 1, то это может быть только чёрный NIL-элемент, так как в случае обычного чёрного элемента высота будет выше.

Таким образом, К1 случай не имеет места быть.

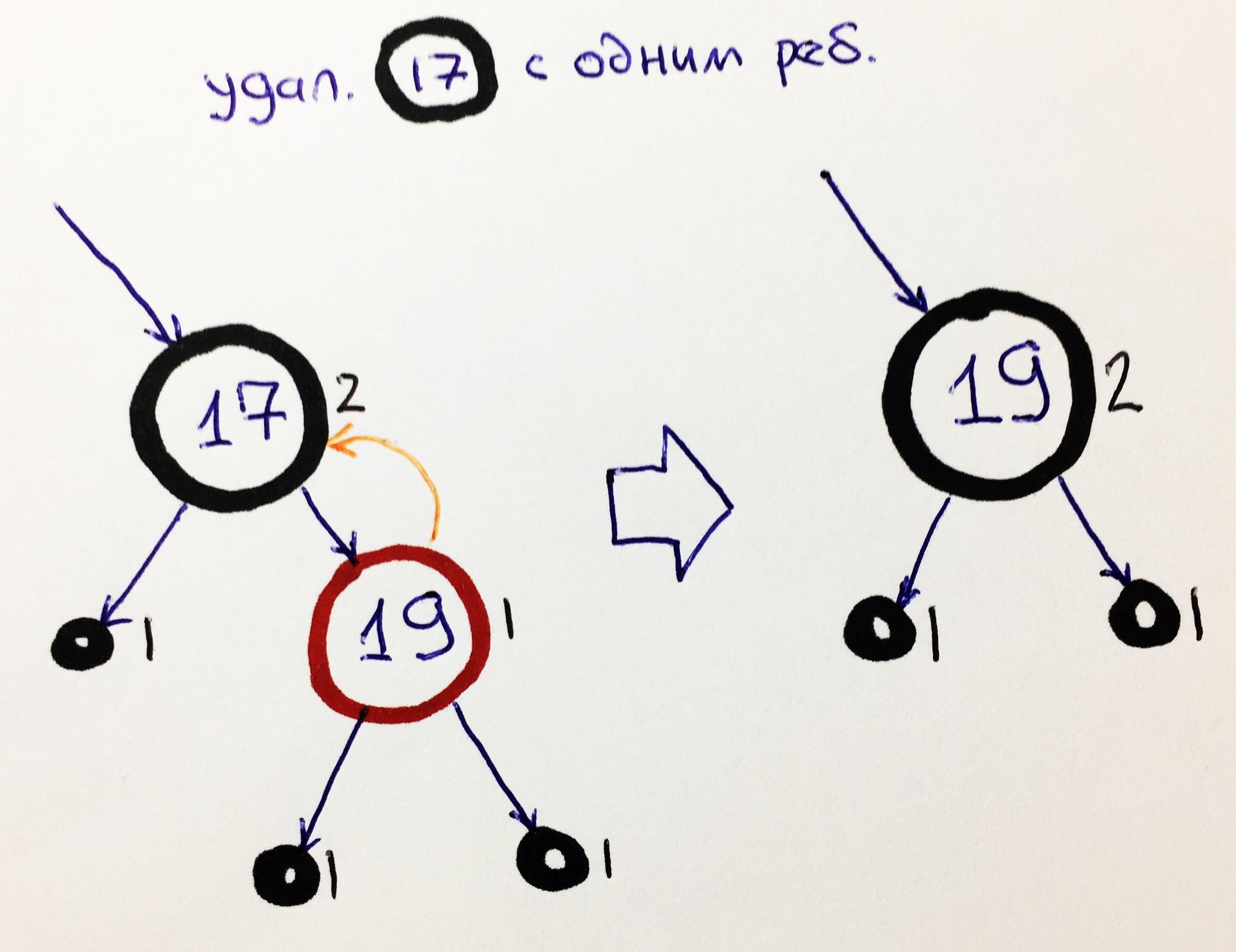
Ч1 — чёрный узел с одним ребёнком

Если у чёрного элемента нет одного ребёнка, значит, вместо него находится чёрный NIL-элемент с чёрной высотой 1. Следовательно, с другой стороны должен быть красный узел без детей. Для удаления такого элемента достаточно перенести значение красного элемента в чёрный узел, чёрная высота при этом сохранится.

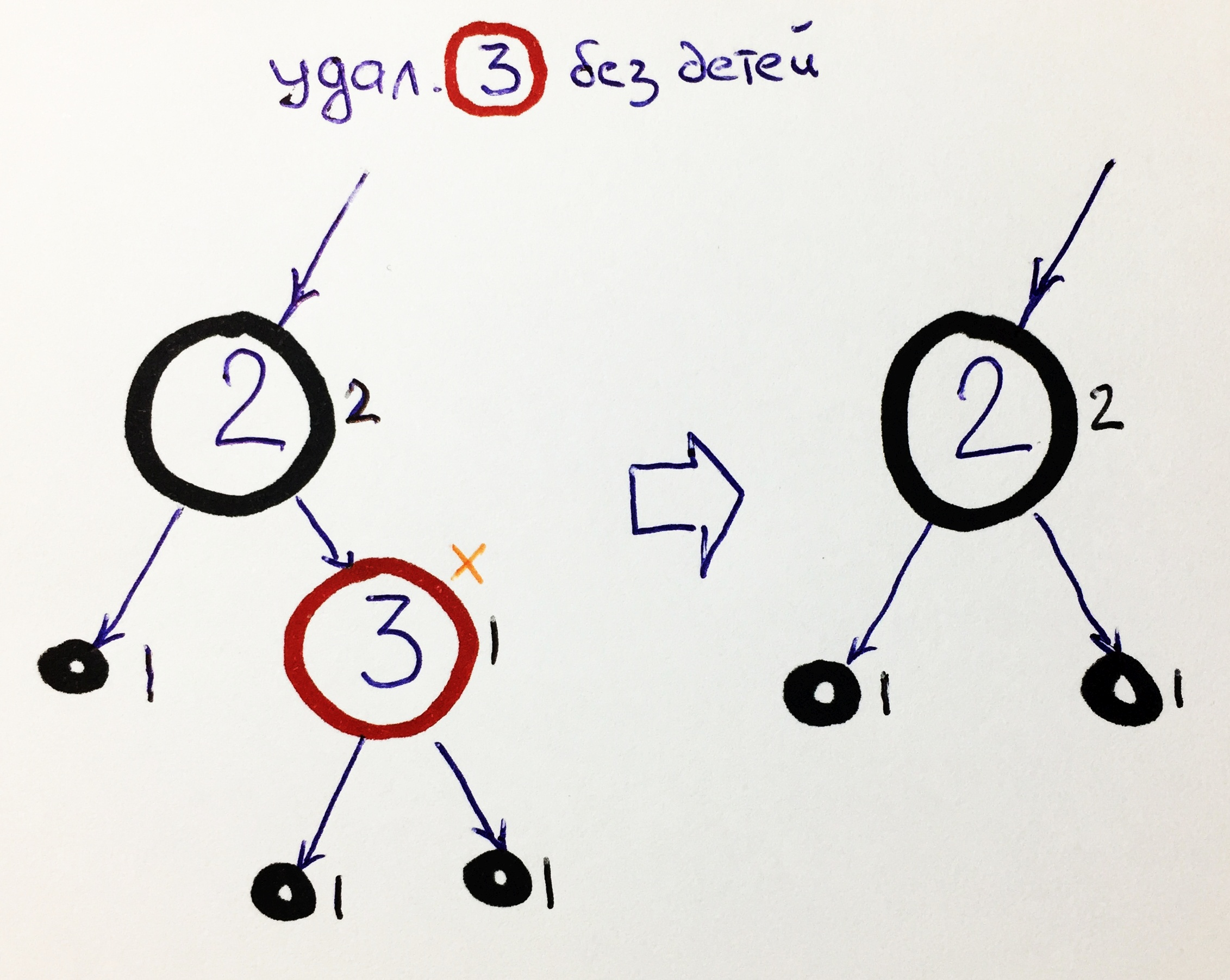
К0 — красный узел без детей

Самый простой случай. Мы просто удаляем элемент, заменяя его ссылкой на NIL:

Удаление красного элемента не изменяет чёрную высоту.

Ч0 — чёрный узел без детей

Удалить чёрный узел без детей тоже очень просто: заменяем его ссылкой на NIL.

Думаете, это уже почти всё? Ха-ха, шесть раз.

После удаления чёрного элемента изменяется чёрная высота поддерева и нужно выполнить балансировку для его родительского элемента.

Удалённый элемент на рисунках обозначается х, его высота – h. Когда мы только начинаем балансировку, то h = 1, но при рекурсивных вызовах она может увеличиться.

Для определённости установим, что удалённый элемент был правым сыном. После удаления его высота уменьшилась и стала h. Значит, высота левого сына осталась h+1. Нам необходимо выровнять высоту левого и правого поддерева и сделать их равными h+1.

Предлагаю снова разделить задачу на несколько частей. Какие у нас могут быть варианты?
Родитель может быть красным или чёрным. Левый сын также может быть чёрным или красным. А правый сын всегда чёрный — именно оттуда мы пришли к балансировке после удаления.

Всего нужно рассмотреть 6 разных случаев:

• КЧ1 и КЧ2 – родитель красный, левый ребёнок чёрный.
• ЧК3 и ЧК4 – родитель чёрный, левый ребёнок красный.
• ЧЧ5 и ЧЧ6 – родитель чёрный, левый ребёнок чёрный.

КЧ1 — родитель красный, левый ребёнок чёрный с чёрными внуками

Пока у нас есть узлы красного цвета, мы можем их перемещать и/или перекрашивать для восстановления баланса чёрной высоты. В этом случае мы можем спустить красный цвет от родителя к левому сыну, выровнив, таким образом, чёрную высоту родителя:

Обязательно перепроверьте по рисунку, что чёрная высота узлов a и b сохранилась, а высота всего поддерева стала одинаковой и равной h+1.

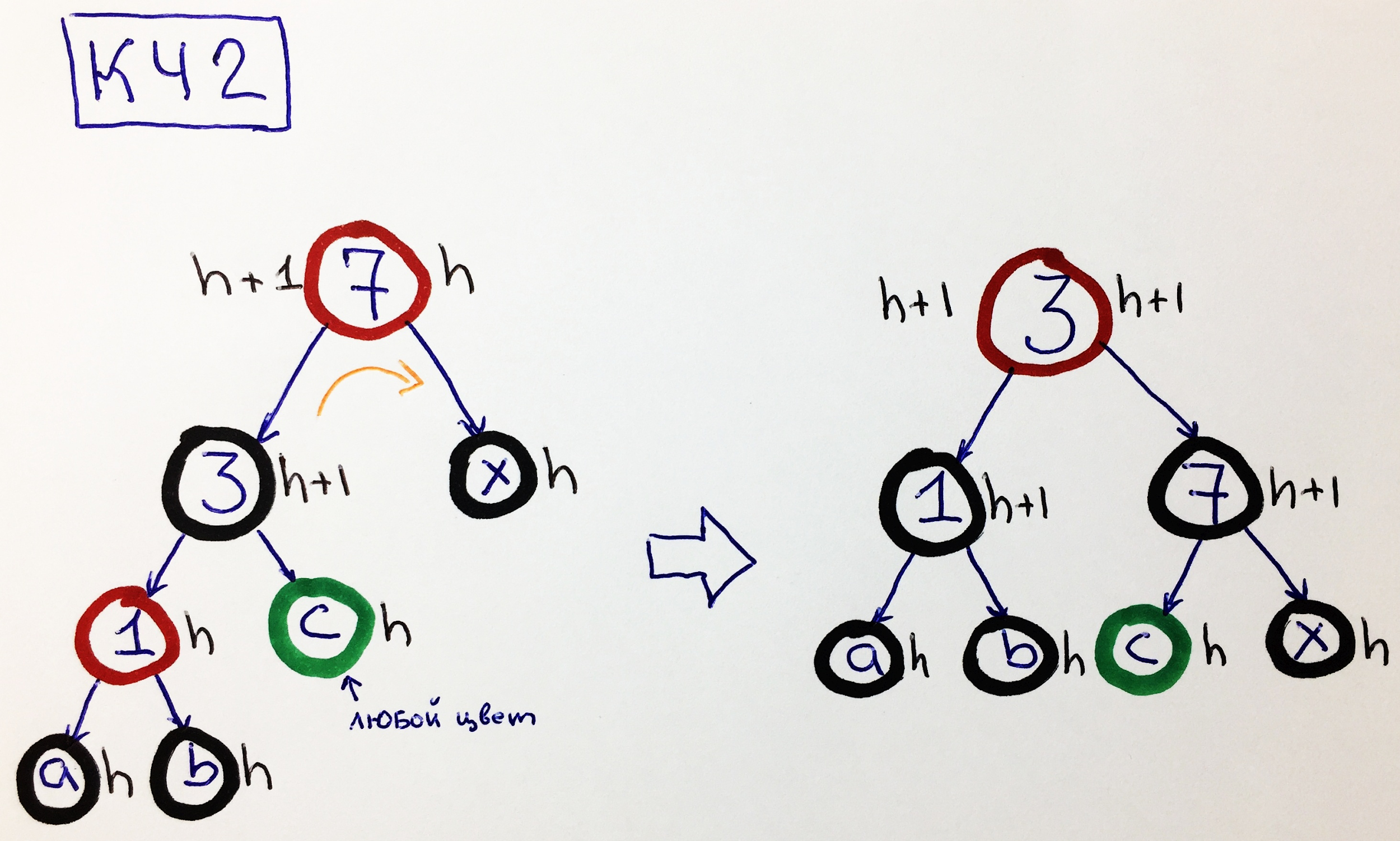
КЧ2 — родитель красный, левый ребёнок чёрный с левым красным внуком.

В этом случае одного перекрашивания недостаточно. Нам нужно выполнить малый поворот направо между узлами 3-7. В результате мы сможем увеличить высоту правого поддерева до h+1:

Зелёный цвет узла означает, что он может быть, как чёрным, так и красным.
Примечание. Если узел “1” будет чёрным, а “с” красным, то задача может быть сведена к варианту ЧЧ5.

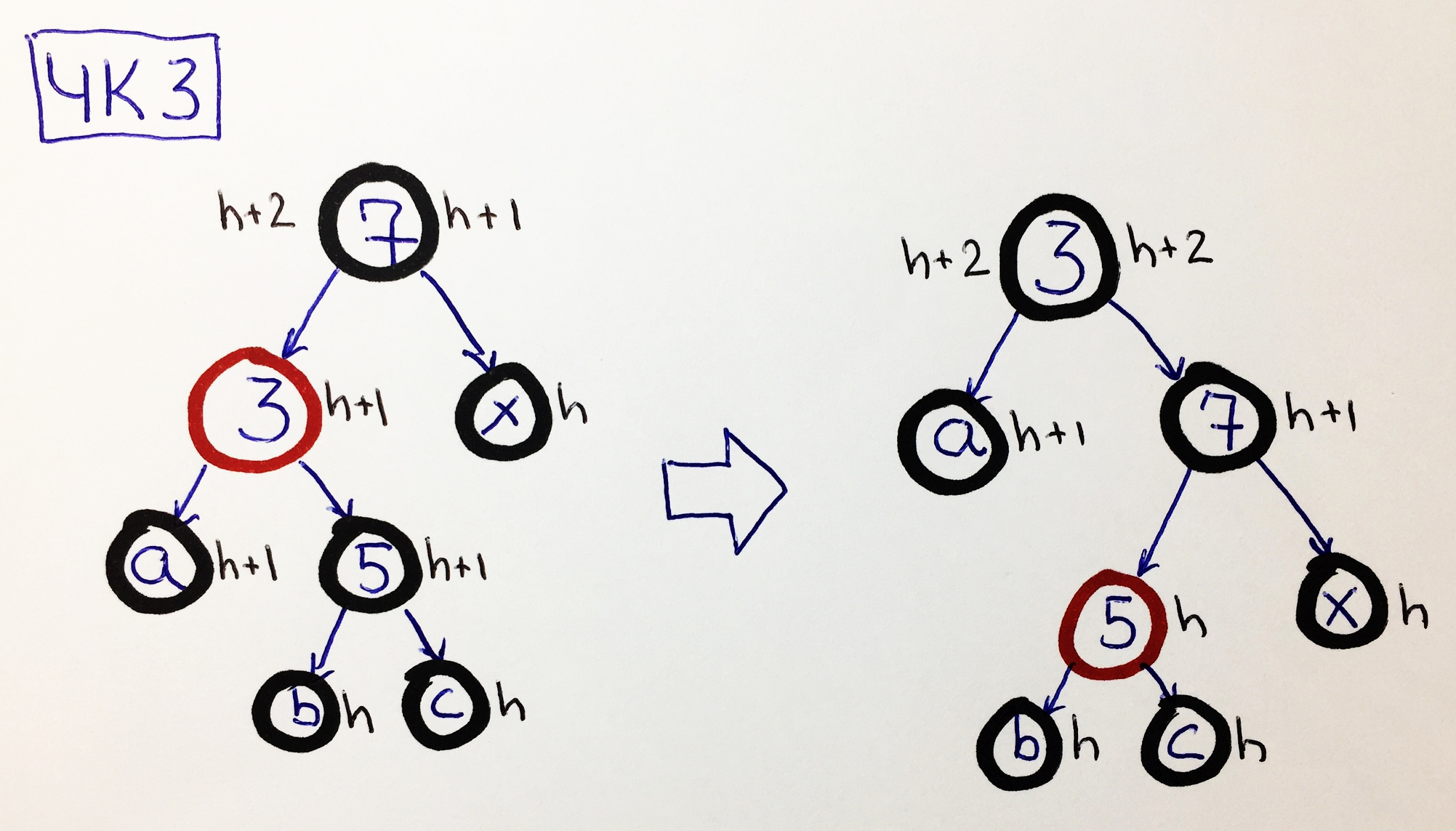
ЧК3 — родитель чёрный, левый сын красный, у правого внука чёрные правнуки

Наличие чёрных правнуков позволяет перекрасить внука в красный цвет и отправить его в правое поддерево, выполнив малый поворот направо 3-7, и не спрашивайте, почему, просто поверьте и проверьте, что чёрная высота стабилизировалась:

Обратите внимание, что красный узел 5 не увеличивает чёрную высоту.

ЧК4 — родитель чёрный, левый сын красный, у правого внука левый правнук красный

Дальше в красный лес — больше чёрных дров, а красных всё меньше, а именно за счёт перекрашивания красных узлов удаётся стабилизировать чёрную высоту.

В этом случае нужно выполнить большой поворот налево, который состоит из двух малых поворотов 5-3 и 5-7. Узел b поменял свой цвет с красного на чёрный и таким образом увеличил свою высоту на 1. Убедитесь, что чёрная высота стабилизировалась.

ЧЧ5 — родитель чёрный, левый сын чёрный с правым красным внуком.

Всё меньше и меньше красных элементов в нашем поддереве, последнего красного внука перекрашиваем в чёрный цвет и выполняем большой поворот налево, как в предыдущем случае.

Проверьте, что чёрная высота поддерева стабилизировалась.

ЧЧ6 — родитель чёрный, левый сын чёрный, его внуки тоже чёрные

И вот настал момент, когда красные дрова закончились. Делать нечего, придётся чёрный узел покрасить в красный и таким образом выровнять чёрную высоту узла 7, но не за счёт увеличения чёрной высоты правого поддерева, а за счёт уменьшения чёрной высоты левого поддерева. В результате чёрная высота всей нашей структуры уменьшится на 1 и мы должны рекурсивно воззвать балансировку к праотцам.

Пример удаления с балансировкой и рекурсией

Мы рассмотрели все 6 случаев балансировки чёрной высоты после удаления элемента из красно-чёрного дерева. Чтобы лучше прочувствовать, как это всё работает, давайте продолжим удаление узла 30 из первоначального дерева.

Первый шаг — просто удаляем узел 30.

Второй шаг — запускаем балансировку на его родителя — узел 25.

С горем пополам стабилизировали высоту узла 25.

Третий шаг — балансировка на дедушкином уровне — для узла 20.

Чтобы было веселее и нагляднее, нарисуем всё дерево до и после балансировки. Имеет место случай ЧК4:

Обратите внимание, как изменилось красно-чёрное дерево после балансировки, часть элементов из левого поддерева перешла в правое, высота стабилизировалась, элемент удалён, все счастливы!

Удаление элементов из красно-чёрного дерева — одна из самых сложных операций при работе с двоичными деревьями поиска. На курсе “Алгоритмы и структуры данных” мы рассматриваем не только двоичные деревья поиска, но и многие другие интересные алгоритмы, подробнее смотрите в программе курса.

Читать ещё

Источник

Красно-чёрное дерево (удалить)

Доказательство: Докажем по индукции. При [math]h=1[/math] получаем дерево, в котором чёрными являются только листья, а их больше одного. Иначе пусть корень — чёрный, тогда оба его поддерева имеют чёрную высоту h-1 и, следовательно, не менее, чем [math]2^[/math] элементов. Тогда всё дерево имеет более [math]2^[/math] элементов. В случае, если корень красный, то оба его поддерева имеют чёрные корни и чёрную высоту [math]h[/math] , то есть, как только что было показано, не менее [math]2^[/math] элементов. Таким образом, дерево будет иметь более [math]2^[/math] элементов.

Доказательство: Возьмём самый длинный путь в дереве. Всего в нём [math]h+1[/math] узлов. По крайней мере половина узлов чёрные, поскольку двух подряд идущих красных узлов быть не может, а лист чёрный. Поэтому чёрная высота дерева не меньше [math](h-1)/2[/math] , и, по первому утверждению, [math]2^[/math] элементов.

Отсюда также получаем, что высота дерева не более [math]2log_2 N+1[/math] , где N — число элементов дерева, т.е. [math]O(log N)[/math]

Операции

• Вставка элемента. Каждый элемент вставляется вместо листа, поэтому для выбора места вставки идём от корня до тех пор, пока указатель на следующего сына не станет nil(т.е. этот сын — лист). Вставляем вместо него новый элемент с nil-потомками и красным цветом. Теперь проверяем балансировку. Если отец нового элемента красный, то достаточно рассмотреть только два случая:

1. «Дядя» этого узла тоже красный. Тогда просто перекрашиваем «отца» и «дядю» в чёрный цвет, а «деда» — в красный. Проверяем, не нарушает ли он теперь балансировку. Если в результате этих перекрашиваний мы дойдём до корня, то в нём в любом случае ставим чёрный цвет.

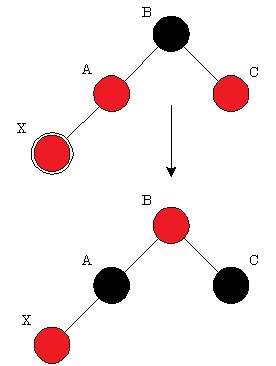
2. «Дядя» чёрный. Если выполнить только перекрашивание, то может нарушиться постоянство чёрной высоты дерева по всем ветвям. Поэтому выполняем поворот. Если добавляемый узел был правым потомком, то необходимо сначала выполнить левое вращение, которое сделает его левым потомком.

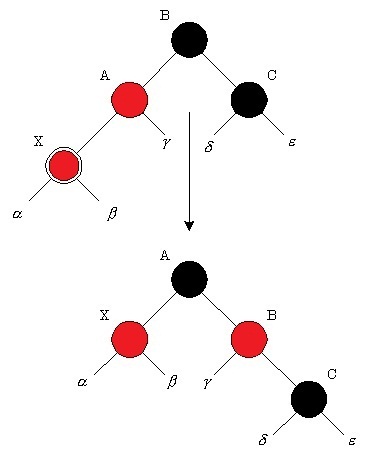
• Удаление вершины.При удалении вершины могут возникнуть три случая в зависимости от количества её детей:

1. Если у вершины нет детей, то изменяем указатель на неё у родителя на nil.
2. Если у неё только один ребёнок, то делаем у родителя ссылку на него вместо этой вершины.
3. Если же имеются оба ребёнка, то находим вершину со следующим значением ключа. У такой вершины нет левого ребёнка. Удаляем уже эту вершину описанным во втором пункте способом, скопировав её ключ в изначальную вершину.

Проверим балансировку дерева. Т.к. при удалении красной вершины свойства дерева не нарушаются, то восстановление балансировки потребуется только при удалении чёрной. Рассмотрим ребёнка удалённой вершины.

1. Если брат этого ребёнка красный, то делаем вращение вокруг ребра между отцом и братом, тогда брат становится родителем отца. Красим его в чёрный, а отца — в красный цвет.

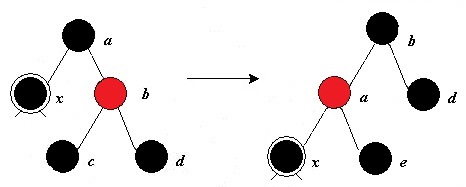
2. Если брат текущей вершины был чёрным, то получаем три случая:

• Если у брата правый ребёнок чёрный,а левый красный, то перекрашиваем брата и его левого сына и делаем вращение.

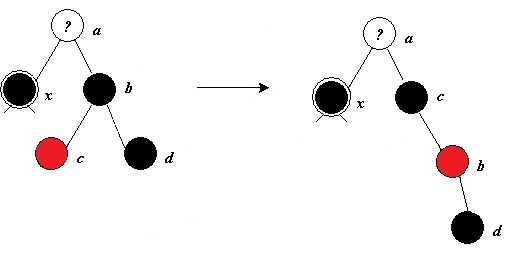
• В же у брата правый ребёнок красный, то перекрашиваем брата в цвет отца, его ребёнка и отца — в чёрный, делаем вращение и выходим из алгоритма.

Продолжаем тот же алгоритм, пока текущая вершина чёрная и мы не дошли до корня дерева. При удалении выполняется не более трёх вращений.

• Объединение красно-чёрных деревьев. Объединение двух красно-чёрных деревьев [math]T_[/math] и [math]T_[/math] по элементу x выполняется, когда [math]key[T_] \leqslant x[/math] и [math]x \leqslant key[T_][/math] .

Найдём чёрные высоты деревьев. Предположим также, что [math]bh[T_] \geqslant bh[T_][/math] . Тогда в дереве [math]T_[/math] ищем среди чёрных вершин, имеющих чёрную высоту [math]bh[T_][/math] , вершину y с наибольшим ключом. Пусть [math]T_[/math] — поддерево с корнем y. Объединяем это дерево с [math]T_[/math] в одно с красным корнем x. Теперь родителем вершины x становится бывший отец вершины y. Осталось восстановить свойства красно-черного дерева, чтобы у красной вершины не было красных детей. Делается аналогично алгоритму добавления вершины.

Т.к. общее время выполнения каждой из операций порядка высоты дерева ,то все они выполняются за [math]O(\log)[/math] .

Источник