Красно черные деревья визуализация

Понимаем красно-черное дерево. Часть 2. Балансировка и вставка

Это вторая часть из серии статей «Понимаем красно-черное дерево». Если вы пропустили первую часть, настоятельно рекомендую ознакомиться с ней здесь. Там мы разобрали причину появления кчд и расставили по полочкам некоторые его свойства.

В данной части мы разберем вставку и балансировку. Эти вещи идут бок о бок, без балансировки дерево будет терять свои свойства, и толка от него будет мало.

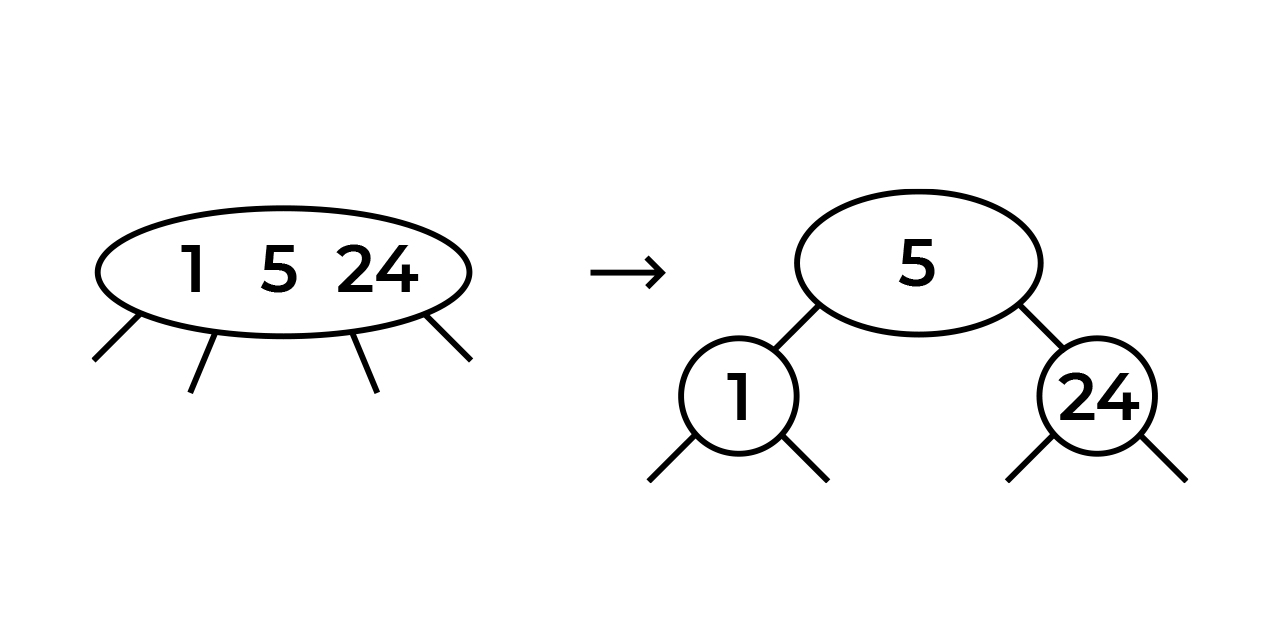
Держа в голове, что кчд — это 2-3 дерево (иногда я буду напоминать об этом), мы сразу начнем с его построения. Но некоторые уточнения все же нужны сейчас.

1. Все вставленные ноды, кроме корня дерева, вставляются с красным цветом. Объясняется это тем, что мы всегда сначала добавляем значение к уже существующей ноде и только после этого занимаемся балансировкой (вспомните ситуацию с получавшимися 4-нодами).
2. В первой части мы выяснили, что разбираем левостороннее красно-черное дерево, из этого следует, что красные ноды могут лежать только слева (обратный случай требует балансировки).

Также давайте разберемся с тремя операциями, которые понадобятся нам при балансировке. Я прошу не задумываться о них сейчас и вникнуть подробнее уже во время построения дерева. Я приведу их описание здесь, чтобы они не мешались потом:)

Первые две операции — это операции поворота. Эти операции также известны как малый левый и правый поворот, например, для АВЛ-дерева. Логика та же, но дополняется все это работой с цветами нод. Третья операция специализирована для кчд деревьев — это переворот цвета или свап цвета.

Если повороты будут для вас не понятны из этой статьи, то информации о них полно в интернете. Я же хочу показать, как ими пользоваться.

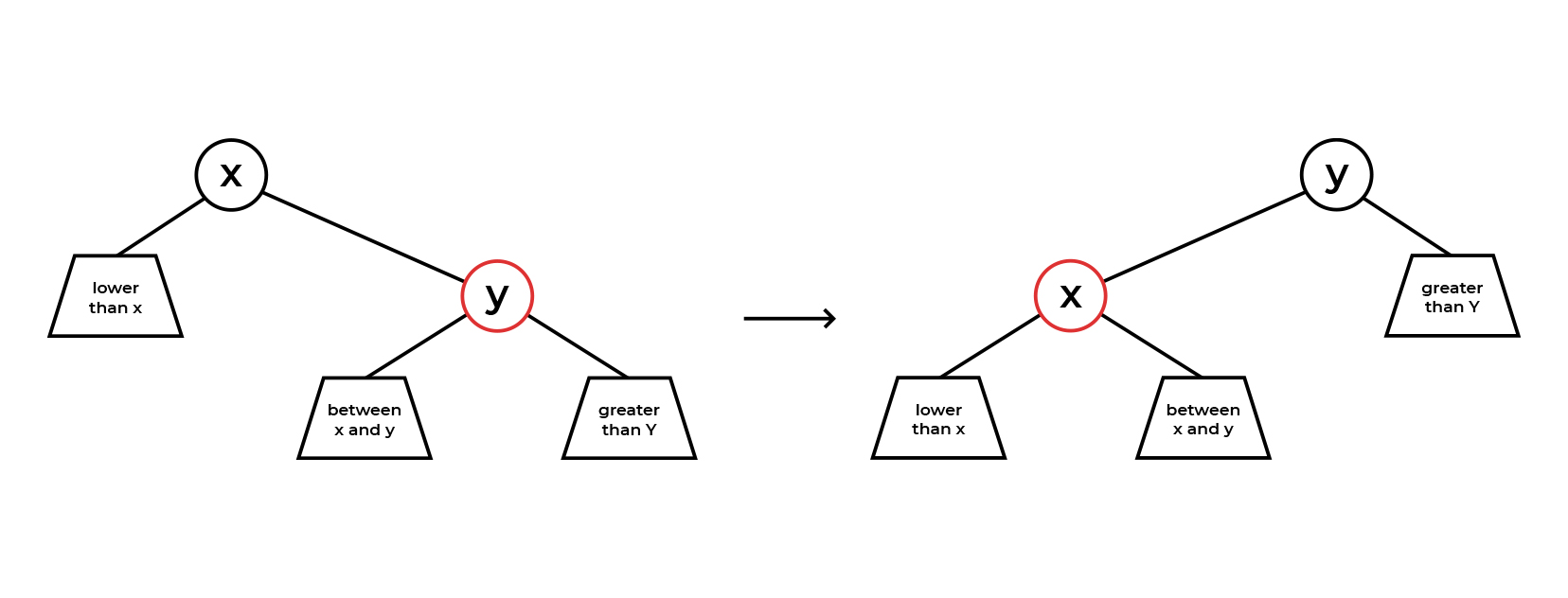
Левосторонний поворот(левый малый поворот)

Здесь мы будем поворачивать наш узел влево. Картинка иллюстрирует поворот операцию.

В первую очередь мы видим, что parentNode (здесь parentNode — это x, childNode — y) не только меняется местом с childNode, но и цветом. Но! Важно уточнить, что, если childNode принимает цвет своего родителя, то цвет parentNode всегда определяется как красный, независимо от предыдущего цвета потомка (левосторонний поворот просходит только тогда, когда цвет childNode — красный, поэтому нам легче сказать, что parentColor = RED, нежели свапать значения). Также обратите внимание на «переезд» левых потомков childNode (да, вам понадобится tempNode). Тут все так же логично, и это не нарушает баланс. Те потомки, что меньше childNode, больше parentNode, и childNode, соответственно, имеют такое же отношение (меньше/больше) к parentNode, как parentNode к своему родителю.

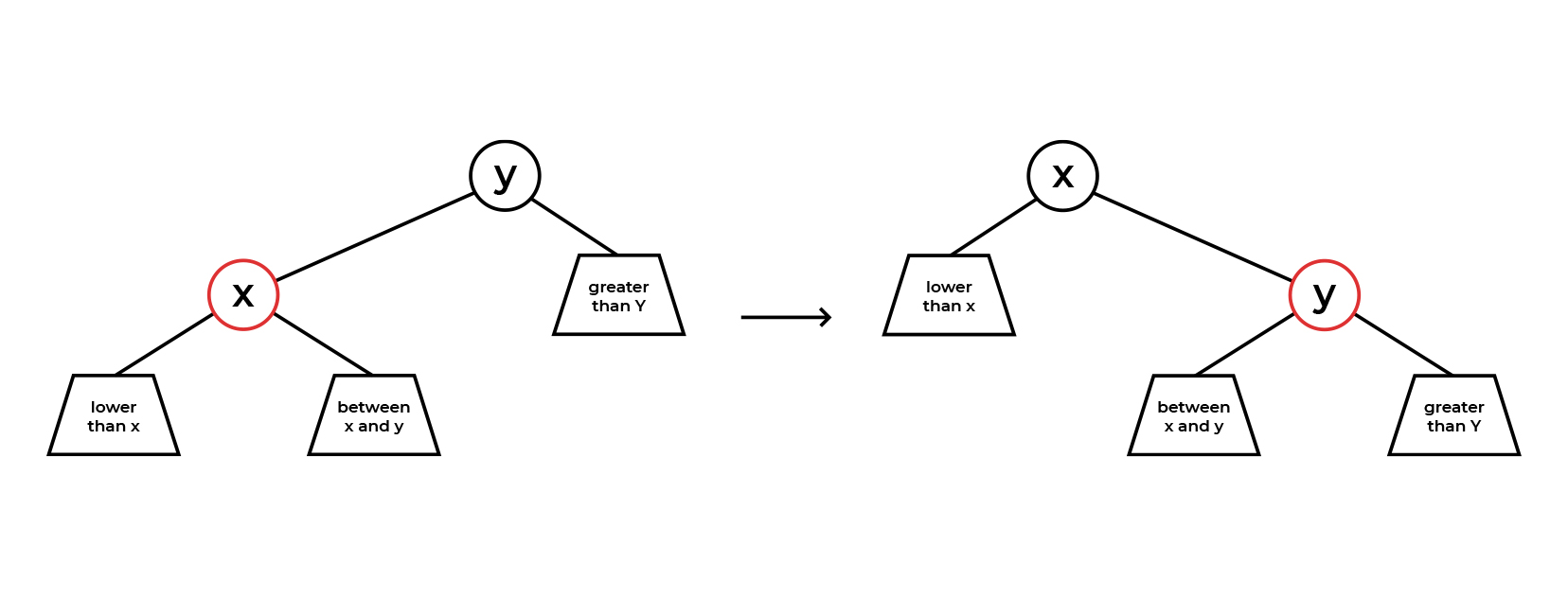
Правосторонний поворот(малый правый поворот)

Тот же поворот, но в другую сторону. Логика аналогична левостороннему.

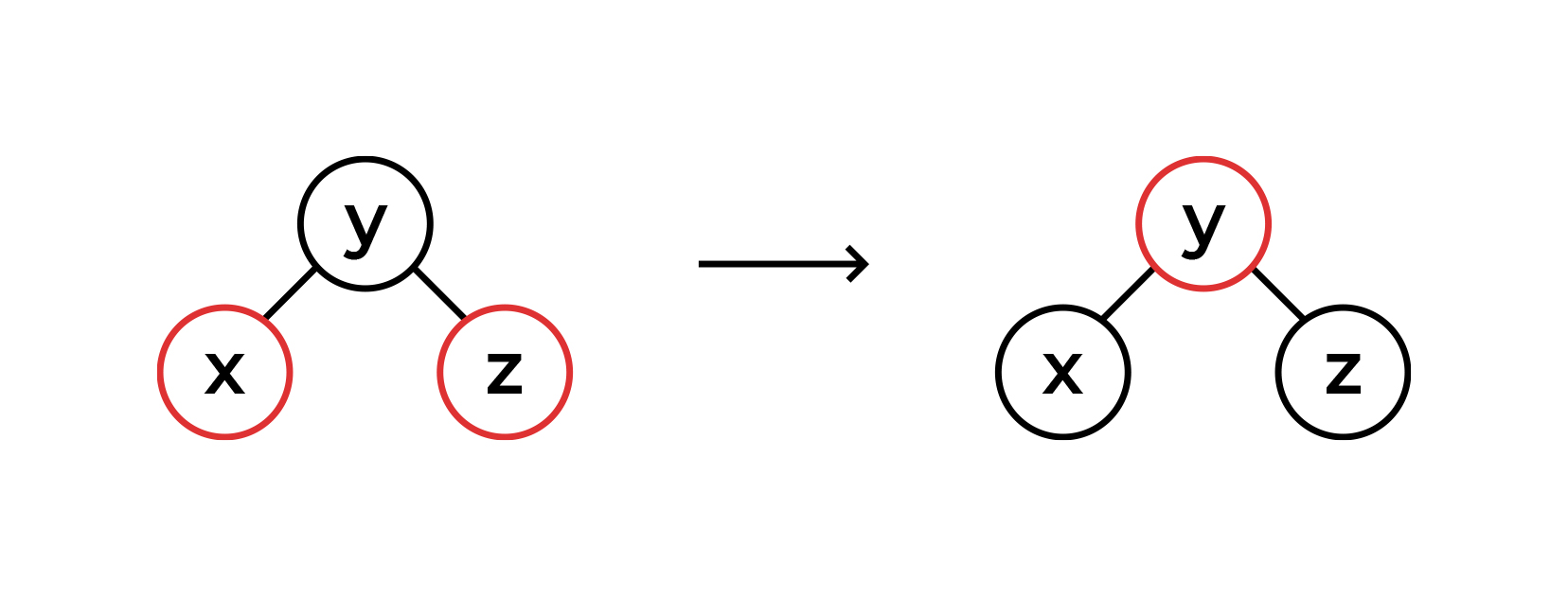
Свап цвета

Свап цвета применяется тогда, когда у parentNode два красных потомка. Потомки становятся черными, а parentNode — красным. Операция легкая, обсуждать тут нечего.

Важно сказать, что все три операции изменяют дерево только локально (свап цвета изменяет ноду на уровень выше, но мы считаем это локальным изменением), и вызываем мы их на уровне parentNode! Мы не теряем сбалансированность на других этажах (если она была). В этом вы можете убедиться самостоятельно.

Построение красно-черного дерева.

Итак, начнем построение нашего дерева.

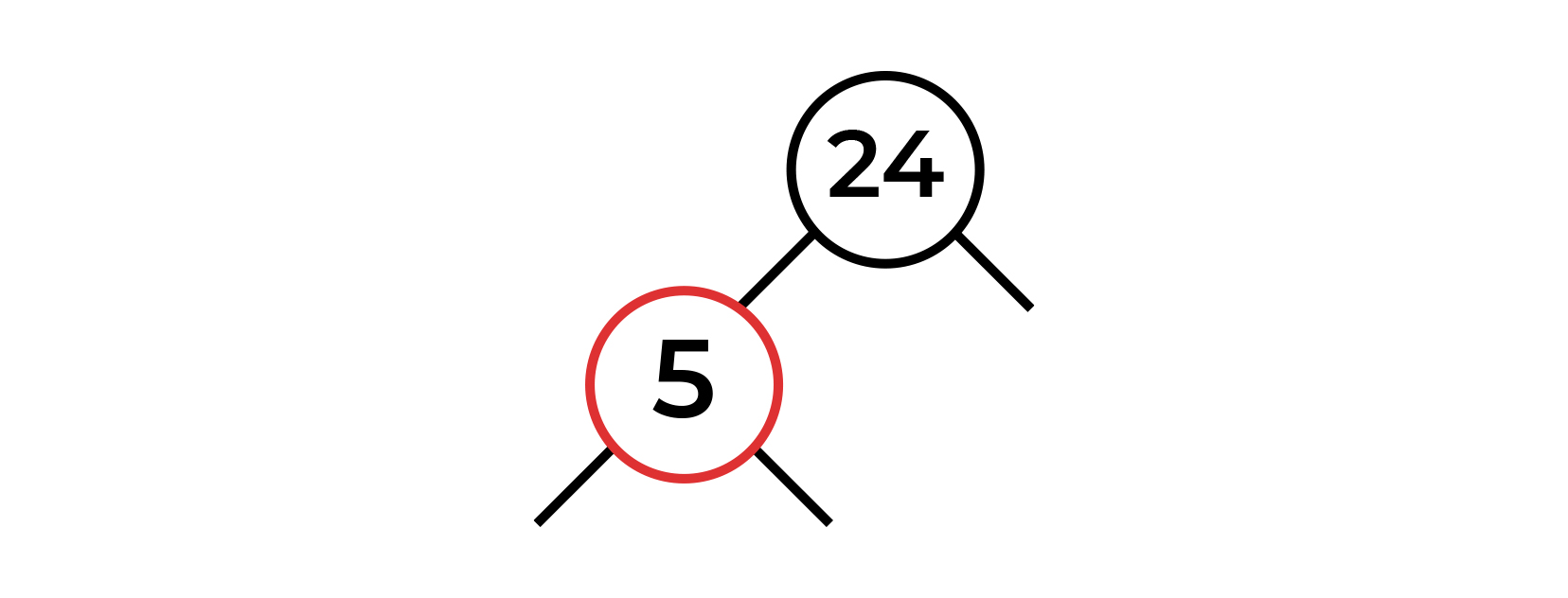
Сначала добавим корень со значением 24. Тут как всегда все просто. Вы помните, что все добавленные ноды имеют красный цвет, кроме корня дерева.

Следующая нода, которую мы вставим, имеет значение 5. По правилу бинарного дерева, нода опускается влево и по правилу кчд становится красной нодой.

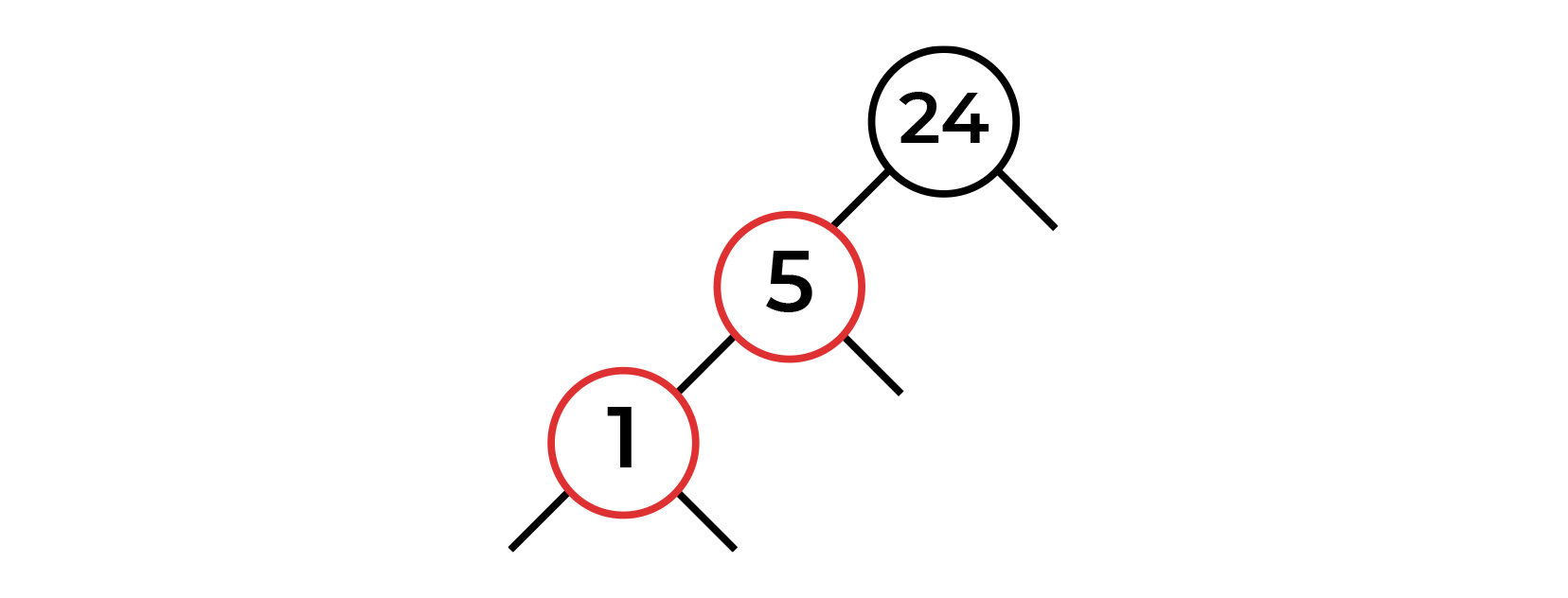
Нода со значением 1 становится потомком ноды 5. Здесь мы видим две идущие подряд красные ноды. В таком случае, нам нужно совершить нашу первую балансировку!

Не секрет, что добавление ноды в дерево — процесс рекурсивный(даже если вы решаете его через циклы). То есть при добавлении ноды мы спускаемся в самый низ. Процесс балансировки же происходит при разварачивании рекурсии — когда мы поднимаемся наверх. Как я уже сказал выше, процесс балансировки — это локальная оперция. Нас не волнует положение дерева ниже\выще нашего уровня. Поэтому я прошу вас абстрагироваться от полной картинки и концентрироваться только на конкретном уровне, когда разбираете балансировку.

В конце этой части я приведу алгоритм и порядок проверок и выполнений операции балансировки для кчд. Но для того, чтобы вы поняли балансировку, а не просто запомнили, давайте попробуем покопаться сами.

Итак, в нашем арсенале 3 операции: правостороний поворот, левостороений поворот, свап цветов.

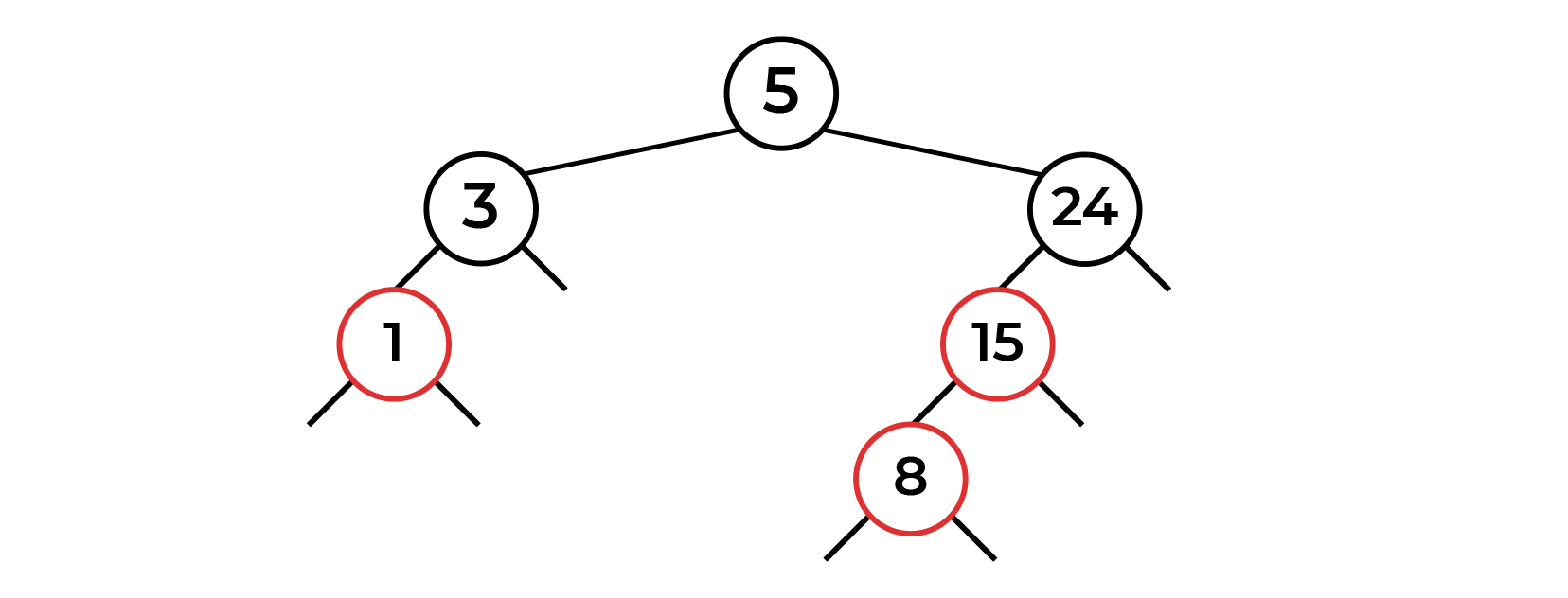
На ноде 1 у нас все в порядке, балансировать нечего. Поднимаемся выше. На ноде 5 так же — одна левостороння красная нода, все корректно (при балансировке мы не смотрим на цвет текущей ноды). На ноде 24 мы уже полностью видим наши подряд идущие красные ноды, значит, нам нужна балансировка.

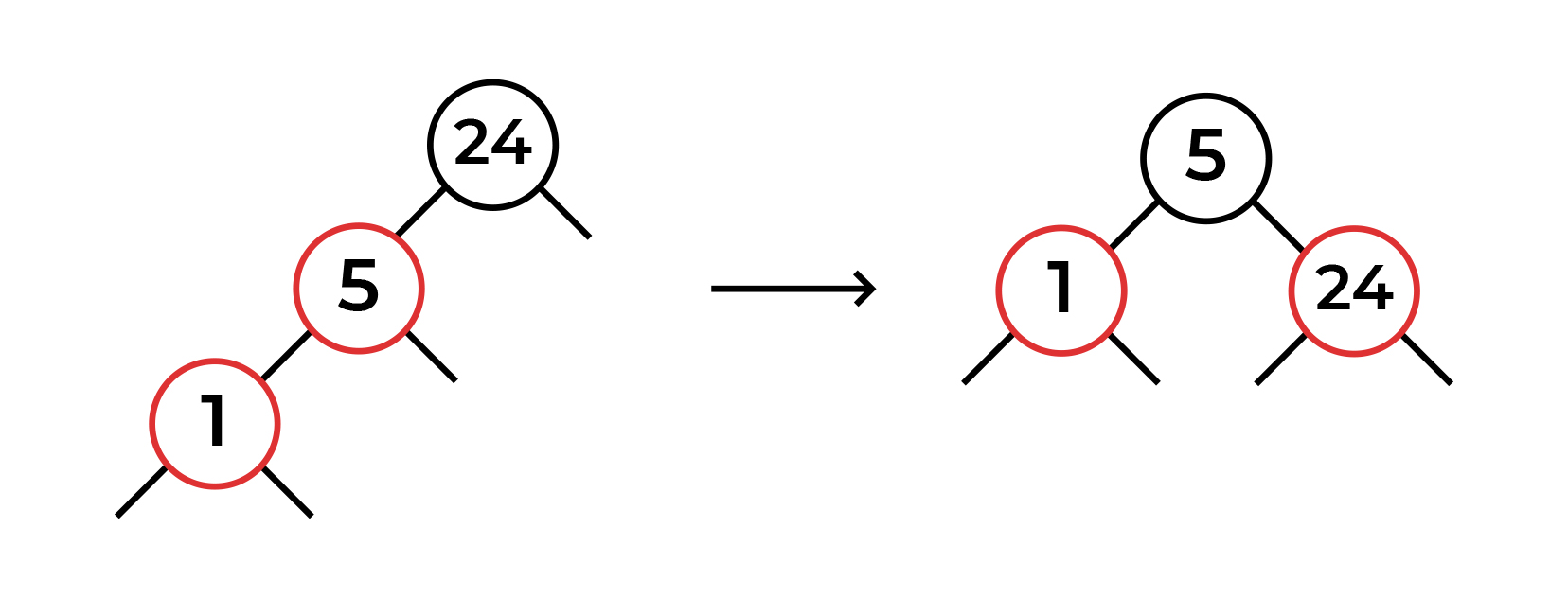
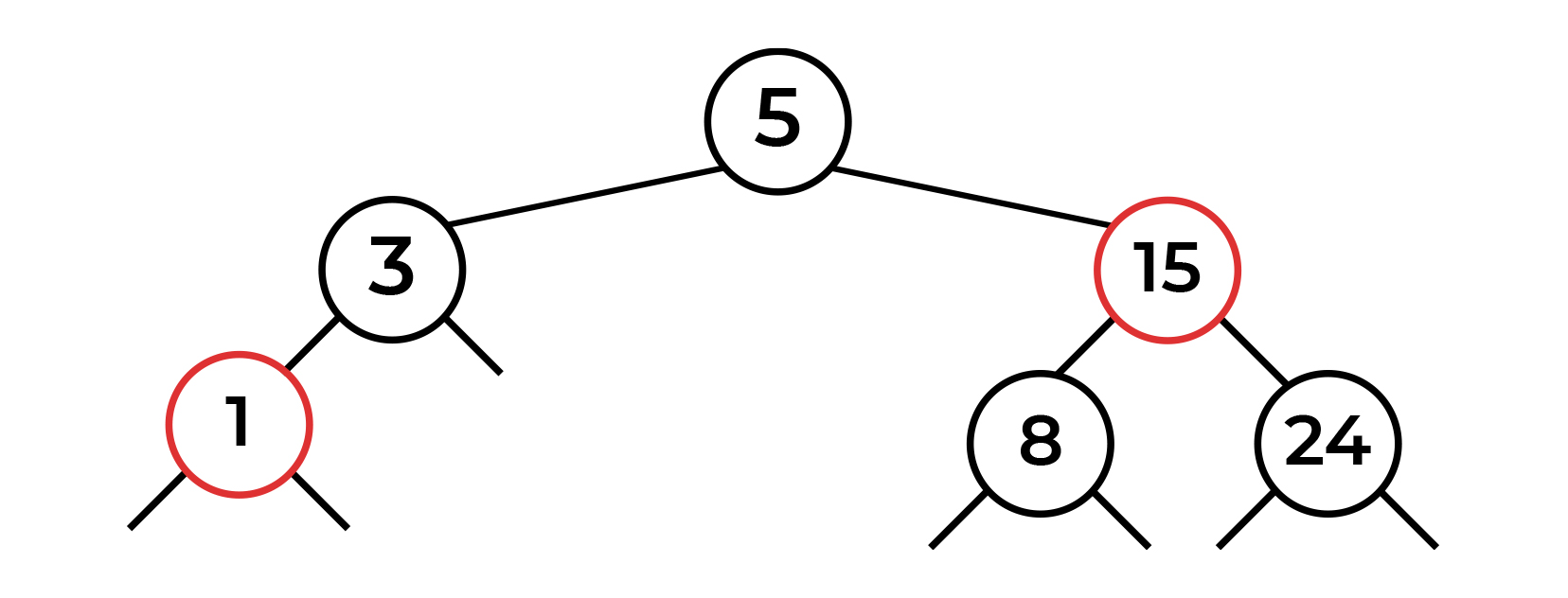
Давайте пока просто попробуем подставить наши операции. Свап цвета нам не подходит — для свапа нужно два потомка с красным цветом. Левостороний поворот не имеет смысла, так как красных нод справа нет. Остается один вариант — правосторонний поворот в ноде 24. Итог вы видите на картинке.

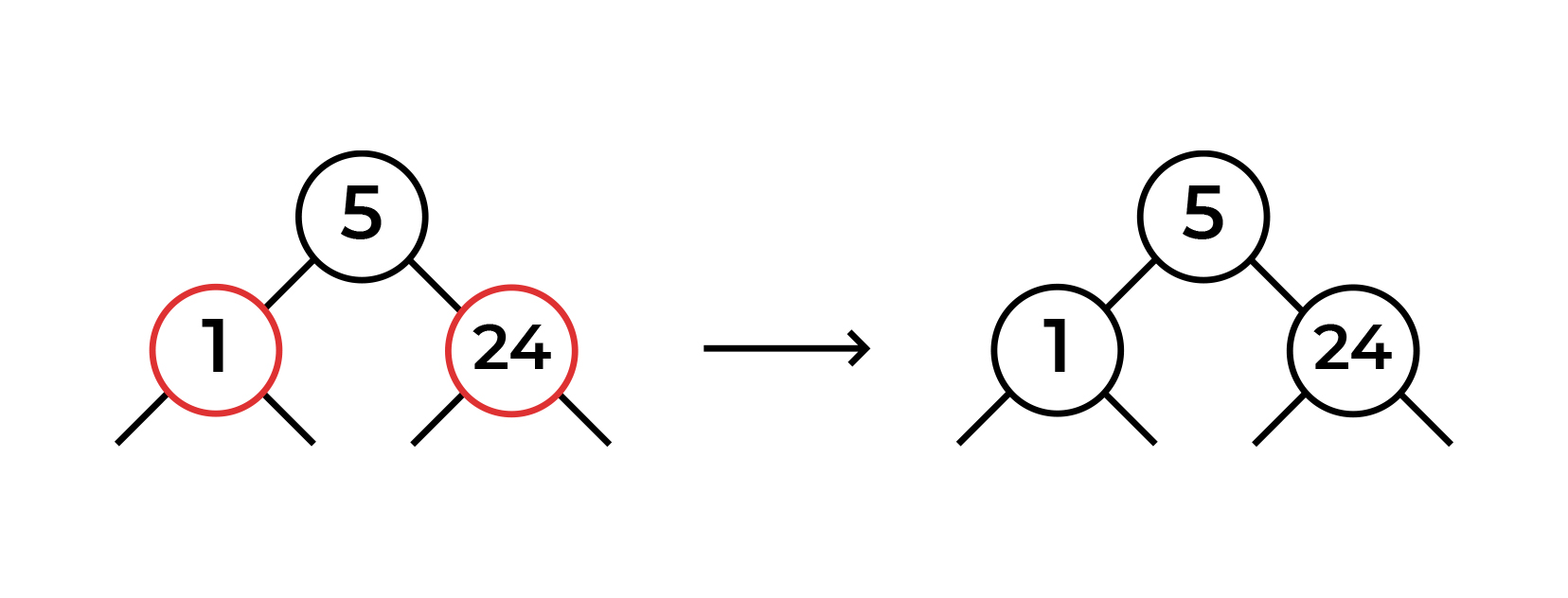
Теперь мы видим, что у корня два красных потомка. Вот здесь то нам и понадобится операция свапа цвета! Результат ниже. (По правилам свапа нода 24 должна была стать красной, но так как это корень, цвет снова стал черным)

В итоге у нас снова корректное левостороннее кчд (и даже без красных нод)! А вот как это выглядело бы в 2-3 дереве.

На картинке видно, что в 2-3 дереве нам нужно меньше операций («просачивание» ноды против поворота + свапа), но это не значит, что на практике сортировать его проще:) Операции вращения, кстати, не имеют аналогов с операциями 2-3 дерева, а операция свапа цвета — это, по сути, наше «просачивание» значения наверх.

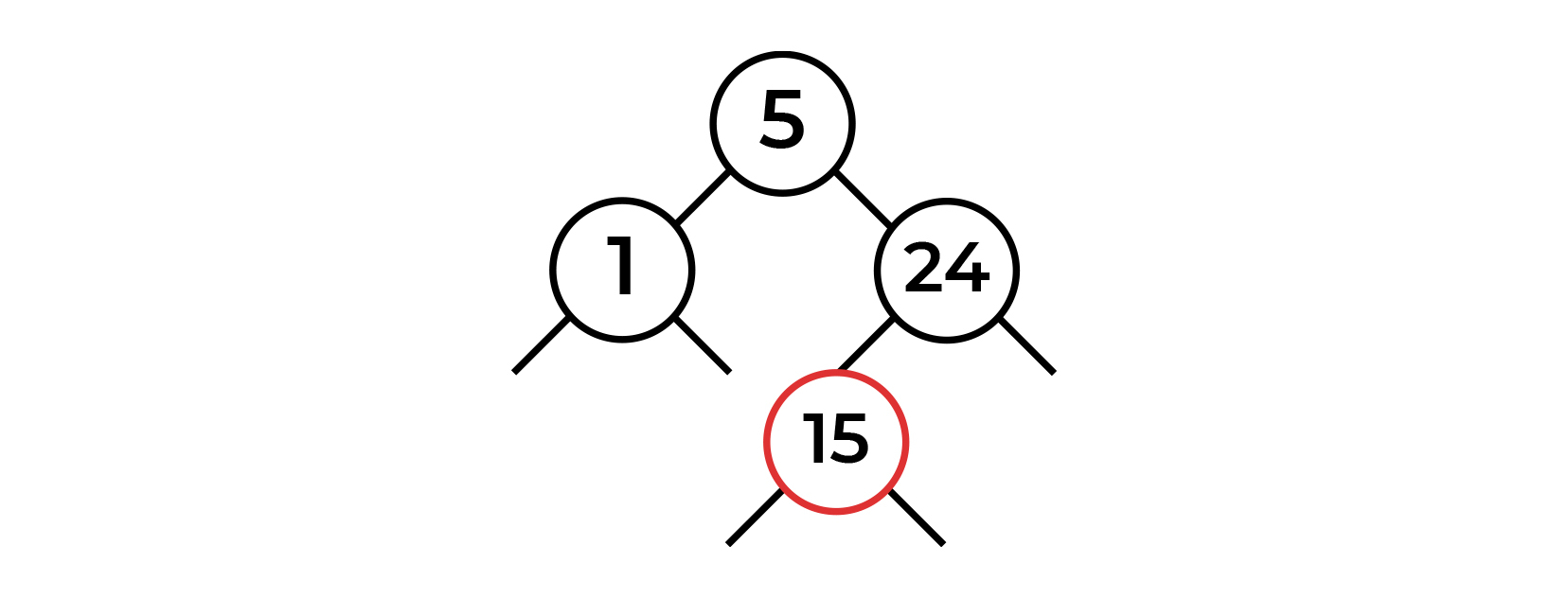
Двигаемся дальше. Вставляем значение 15. Нода уходит в левого потомка ноды 24. Здесь балансировка не нужна.

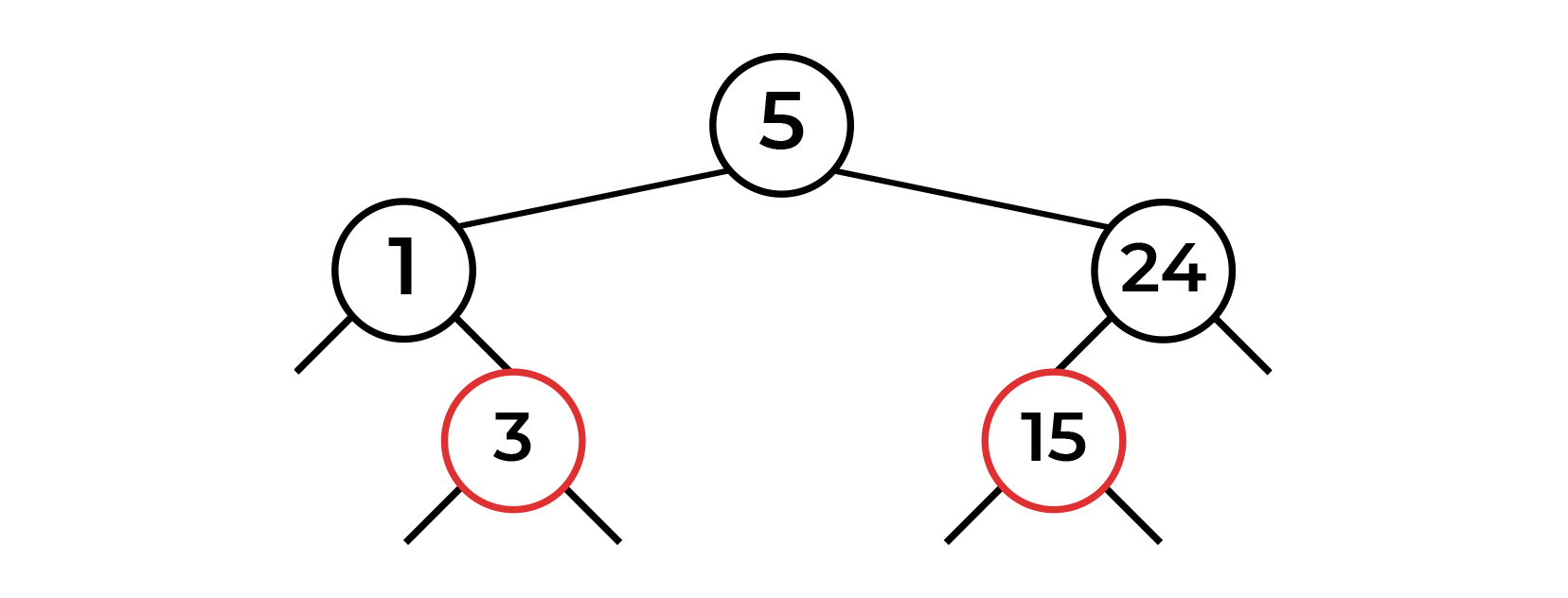
Вставляем 3. Нода будет меньше корня, но уже больше 1, поэтому нода становится правым потомком ноды-1.

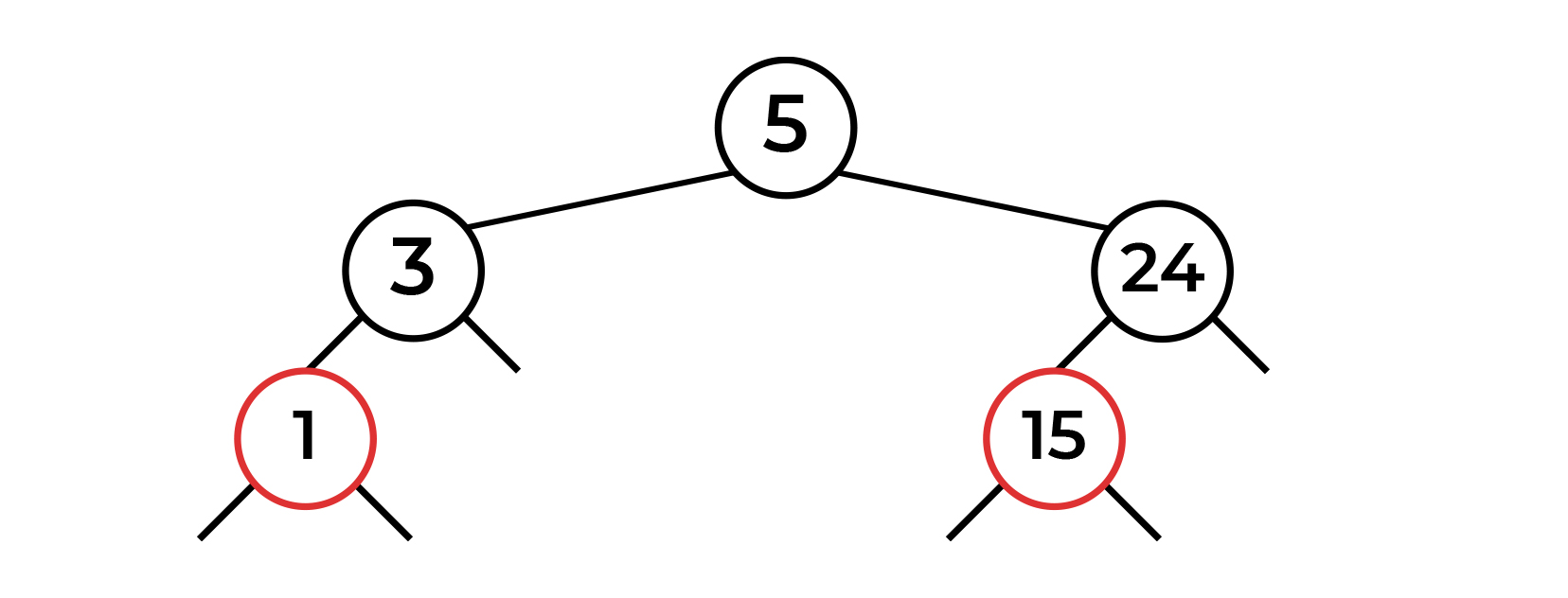
Как мы видим, красная нода находится справа. И снова балансировка. В прошлый раз нас спасла комбинация правосторонний поворот + свап цвета. В этот раз поворот в право нас не спасет (как и свап цвета, я думаю, это очевидно). Сделаем поворот влево и посмотрим, что получится.

Вуаля! Наше дерево снова корректно.

Я думаю, что уже сейчас вырисовываются какие-то правила и закономерности действий, но давайте не будем торопиться и рассмотрим еще пару примеров.

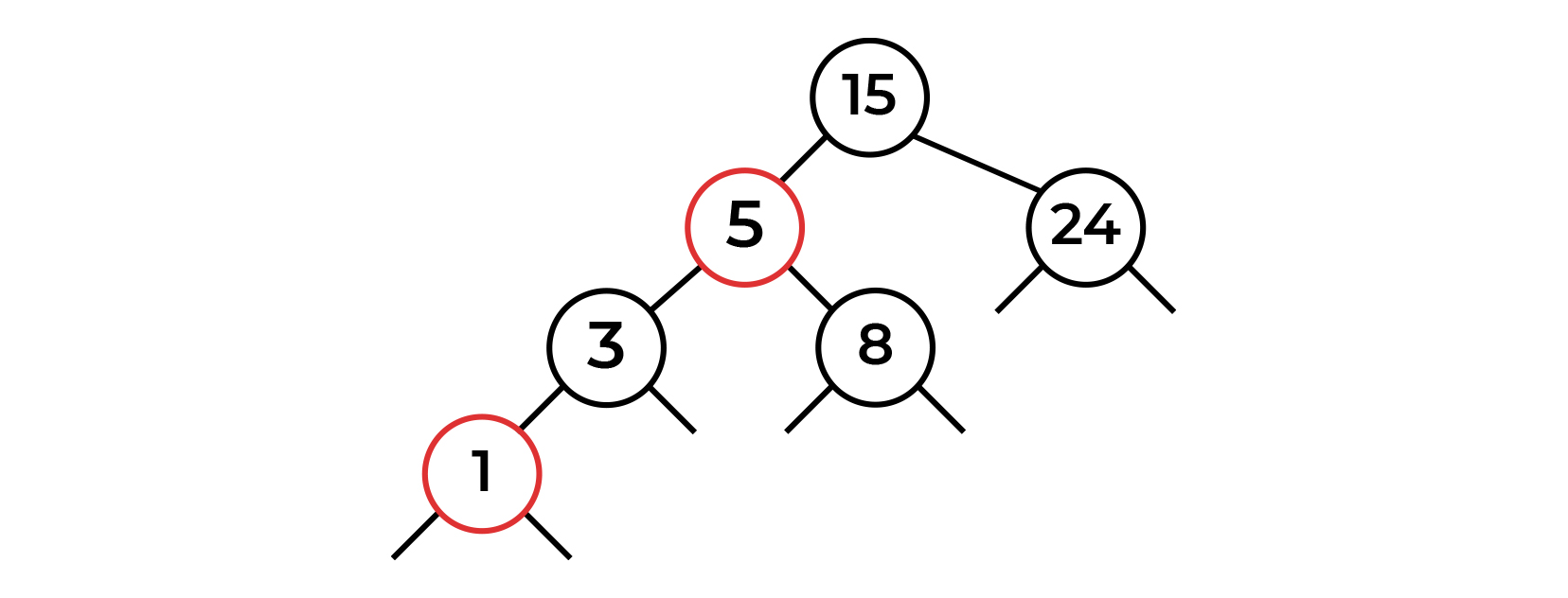
Последнее наше значение — 8. Куда оно встанет, догадайтесь сами. Результат мы видим на картинке. Такая ситуация нам уже встречалась, и мы знаем, что делать.

Правосторонний поворот + свап цвета дает нам следующий результат.

Видим, что на нашем уровне(нода 15) ситуация стала лучше — сама нода красная, оба потомка черного цвета. Условия валидны. Поднимаясь на уровень выше, мы снова видим проблему — красная нода справа. Как это решить мы также знаем. Левосторонний поворот!

Ожидаемый итог — снова корректное левостороннее красно-черное дерево.

Вам может показаться, что дерево перестроилось кардинальным образом. Но если приглядеться, то станет понятно, что это не так. Последний левосторонний поворот поменял наше дерево лишь на одном уровне. Все остальные ноды остались на месте.

Вот в целом и все. За исключением пары моментов, построение дерева будет выглядеть примерно так. Как и в случае 2-3 дерева попробуйте сейчас сами добавить пару значений в дерево (ноды 13 и 16, например, интересный случай).

Как я уже говорил выше — операция балансировки это дело локальное, поэтому мы не думаем и не должны думать о том, что происходит на этаж выше\ниже. Это очень удобно при написании кода.

Ниже в спойлере я приведу алгоритм, на который можно опираться при написании кода, а вы можете попробовать привести решение сами.

Алгоритм балансировки кчд

1. если правая нода красная и левая нода черная — левосторонний поворот
2. если левая нода красная и левая нода левой ноды красная — правосторонний поворот
3. если левая нода красная и правосторонняя нода красная — делаем свап цвета.

Все использования операций логичны — вращаем ноду влево, если красная нода справа. Вращаем ноду вправо, если две красные ноды идут подряд, чтобы потом сделать свап цвета. Не старайтесь запомнить это, постарайтесь понять!

Теперь вы можете пробежаться по построению дерева еще раз и проанализировать, свериться со свойствами из первой статьи, задаться вопросами «а что будет если. » (поверьте, это очень полезно!). В целом, это все, что я хотел рассказать вам про вставку ноды в левостороннее красно-черное дерево.

Немного об операции поиска значения

Операция получения ничем не будет отличаться от поиска в любом другом бинарном дереве — цвет тут никак не участвует.

Заключение

На этом я закончу нашу вторую часть про вставку и балансировку кчд. Задавайте свои вопросы, критикуйте и дополняйте статью ниже! В заключительной, третьей, части я расскажу про самую сложную тему красно-черного дерева — удаление элемента. До встречи:)

Источник

Красно-чёрные деревья на javascript

Привет Хабр! Изучал недавно красно-черные деревья. Попробовал визуализировать детали работы алгоритмов вставки и удаления на d3.js. Надеюсь, полученный результат поможет сэкономить немного времени тем, кто изучает алгоритмы на javascript. Посмотреть можно тут. Исходник реализации, от которой отталкивался тут . Под катом краткие подробности.

Поиск существующих решений

Главной целью задумки было разобраться в реализации алгоритма и визуализировать ее. Первым делом стал искать реализацию с полными и понятными пояснениями и кодом на js. В процессе поиска опечалило, что авторы временами недоделывают исходник, например, тут есть алгоритм вставки, но нету удаления. Или делают визуализацию как тут , но не дают ссылки на исходник. Потом нашел вот эту отличную статью. Но хоть убейте, до сих пор не могу понять почему автор вставил код картинками и не дал по запросу в коментах ссылку на исходник. Есть еще npm пакет red-black-tree , весь исходный код которого: ‘in progress. ‘ в readme. Также нашлась популярная реализация красно-черных деревьев на js, от которой зависит куча пакетов и миллионы закачек в неделю, но код там устарел лет на пять.

Расстановка приоритетов и конкретизация задачи

Пораскинув мозгами, решил, что читаемость и понятность кода для учебных целей приоритетнее, поэтому взял за основу статью, которую упоминал вначале, а не npm пакет. Реализация оказалась более удобной и наглядной в плане чтения кода. В статье автор начинает с двоичного дерева, потом расширяет его до красно-черного. Для визуализации выглядит вполне логичным наследовать от красно-черного дерева и сделать анимированное дерево. Поэтому, перенабрав код и убедившись, что он работает, приступил к рисованию анимированного дерева. Дальше на помощь приходит d3.js. Там есть замечательные transitions, которые позволяют двигать элементы в нужные позиции и плавно трансформировать в подходящие состояния, по ходу работы алгоритма.

Смысл красно-черных деревьев

Долго думал, как бы по простому, объяснить что к чему. Наверное, все таки надо почитать теорию из разных источников. Как говорится: «Из песни слов не выкинешь». Но простые итоговые выводы в двух словах сформулировать можно. Суть сводится к тому, что есть несколько кейсов при вставке и удалении элемента, в зависимости от которых «дедушки», «папы», «дяди», «дети», «братья» перекрашиваются и сдвигаются (поворачиваются) в сторону, где элементов меньше. В результате никогда не бывает, чтобы путь от самого дальнего узла к корневому был слишком длинным, поэтому поиск нужного элемента в такой структуре происходит очень быстро. Ну а компенсируется это сложностью вставки и удаления.

Источник