Какие критерии информативности используются при синтезе решающего дерева и почему?
Дерево решений — это контролируемый алгоритм обучения, используемый как для задач классификации, так и для задач регрессии. Проще говоря, он принимает форму дерева с ветвями, представляющими возможные ответы на заданный вопрос. Существуют метрики, используемые для обучения деревьев решений. Одним из них является получение информации
Можно определить прирост информации как меру того, сколько информации предоставляет функция о классе. Получение информации помогает определить порядок атрибутов в узлах дерева решений. Главный узел называется родительским узлом, тогда как подузлы называются дочерними узлами. Мы можем использовать прирост информации, чтобы определить, насколько хорошо разделение узлов в дереве решений. Это может помочь определить качество расщепления.Расчет прироста информации поможет лучше понять эту концепцию.
Термин Gain — «выигрыш» означает прирост информации. Eparent — это энтропия родительского узла, а E_
Чем больше удалено энтропии, тем больше прирост информации. Чем выше прирост информации, тем лучше разделение. В качестве родительского (корневого) узла следует выбрать атрибут с наибольшим информационным приростом из набора.
Создавайте дочерние узлы для каждого значения атрибута A, следуя тому же принципу. Повторяйте итеративно, пока не закончите построение всего дерева.
Источник
Критерии качества для построения решающих деревьев
На предыдущем занятии мы с вами познакомились с общей идеей логических методов. Здесь же продолжим эту тему и подробнее поговорим о бинарных решающих деревьях. Приведу пример такого дерева из предыдущего занятия:
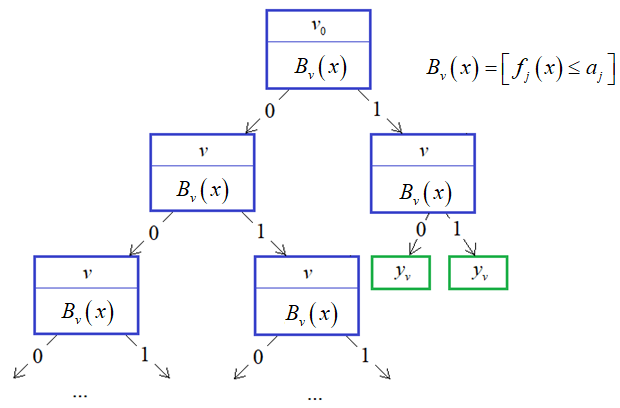
Фактически это связный ациклический граф, в котором есть корень, внутренние вершины и листы (вершины без потомков). Причем, каждая внутренняя вершина имеет ровно два ответвления, соответствующие стрелкам «да» и «нет». Именно поэтому дерево с такой структурой называют бинарным.
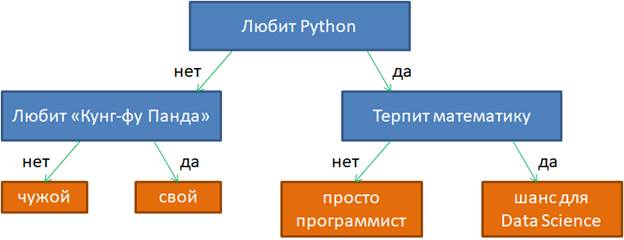
Если у нас есть уже построенное дерево по множеству данных, то логический вывод делается очень просто. Предположим, мы классифицируем вектор
с n признаками. Тогда, начиная с корневой вершины , проверяем предикат:
То есть, мы смотрим на j-й признак для вектора 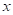
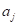
В следующей промежуточной вершине повторяем этот процесс и с помощью предиката проверяем значение другого j-го признака (или того же самого). В зависимости от ответа, переходим или по стрелке 1, или по стрелке 0.
Как только дошли до листа, относим вектор к тому классу, который прописан в текущем листе. Процесс логического вывода на этом завершается. Именно поэтому листовые вершины еще называют терминальными.
Однако, чтобы проделать такой вывод, мы с вами должны знать структуру дерева, набор предикатов для каждой промежуточной вершины и иметь правильные значения в листовых вершинах. Листы дерева, как правило, хранят определенные числа. Они могут означать или номер (метку) класса, или константное значение функции при решении задач регрессии. Но пока будем полагать, что в них записаны метки класса.
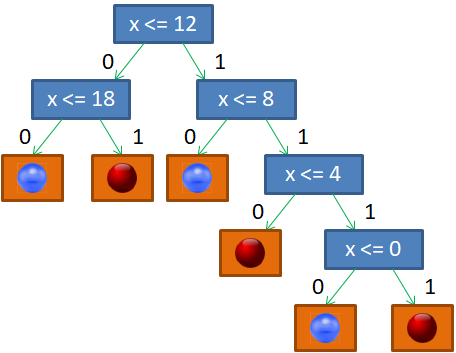
Итак, главный вопрос, как построить бинарное решающее дерево по множеству данных обучающей выборки ? Чтобы лучше понимать этот процесс, давайте возьмем очень простой пример разбиения последовательности красных и синих шаров, собственно, на красные и синие:
Здесь вектор состоит из одной компоненты и представляет собой число – номер позиции шара. Это единственный признак, по которому можно выполнять разбиение данной последовательности. В каждой промежуточной вершине бинарного решающего дерева будет использован предикат вида:
И, так как признак всего один, то . Остается найти только нужные пороги t.
Если бы разбиение делал я сам, то предложил бы следующее решающее дерево:
Почему именно так? В действительности, можно было бы придумать и другие варианты. Я руководствовался простым принципом: в каждой вершине порог t следует выбирать так, чтобы в одной части было как можно больше представителей только одного какого-либо класса (шаров одного цвета), а в другой – все оставшиеся. То есть, это некий критерий здравого смысла, естественная эвристика, которая сокращает глубину дерева. Но вы можете сказать, а зачем нам минимизировать глубину решающего дерева? Пусть оно получается таким, каким сделает его алгоритм. Например, будем поочередно перебирать пороги t от 0 до 19 и рано или поздно гарантированно разобьем последовательность шаров на красные и синие. Да, дерево будет значительно глубже, ну и что? Однако, здесь всегда следует помнить, что данная последовательность всего лишь обучающая выборка. Мы предполагаем использовать это дерево и для других подобных последовательностей с несколько другим распределением синих и красных шаров. Иначе, это была бы не задача машинного обучения, а просто разбиение конкретной выборки. Так вот, можно заметить, что чем меньше глубина решающего дерева, тем меньше используется порогов разбиения и тем выше, в среднем, обобщающая способность такого дерева. Именно поэтому стараются строить деревья минимальной глубины.
Но как это сделать? В самом простом варианте можно выполнить полный перебор всех возможных разбиений и выбрать дерево минимальной глубины. Для нашей задачи это еще как-то можно было бы реализовать. Но, как вы понимаете, в общем случае, это займет так много времени, что не хватит и жизни всего человечества. Поэтому здесь нужно искать другие подходы.
Если вернуться к моему варианту бинарного дерева, то, как я отмечал, в каждой промежуточной вершине старался порог t выбирать так, чтобы в одной части было как можно больше представителей одного класса (шаров одного цвета), а в другой как получится, т.е. все оставшиеся. Это некая эвристика. Наша цель, наделить алгоритм примерно такой же эвристикой. Как это сделать? Математики обратили свои взоры в ранние наработки самых разных формул и представили миру несколько критериев качества предикатов. Одним из популярных стала энтропия:
где — вероятность i-го класса; N – общее число классов (в нашем примере – цветов шаров). Известно, что эта величина является некой характеристикой хаотичности системы. Чем больше разнообразия, тем выше энтропия, и наоборот, чем больше порядка, тем она меньше. Ее можно естественным образом использовать для оценки характеристики текущего разбиения каждой вершины. Например:
Такую характеристику в решающих деревьях называют impurity (информативностью). Чем она меньше, тем лучше (качественнее) набор данных в вершине. И, наоборот, чем она больше, тем разнообразнее (хаотичнее) данные в вершине.
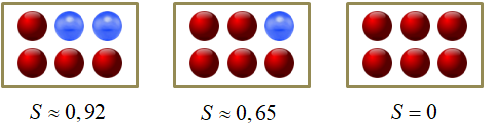
Вернемся, теперь, к примеру разбиения последовательности красных и синих шаров. Последовательность состоит из N=2 классов с вероятностями появления каждого из них:
Следовательно, impurity (в данном случае энтропия) корневой вершины дерева, равна:
Далее, мы выбираем предикат с порогом t = 12:
и получаем две подвыборки с impurity (энтропиями):
Величина 0,6 значительно меньше начального значения 0,993, а значит, во второй последовательности больше порядка, чем в исходной. И это очень хорошо. Именно этого мы и добиваемся, выбирая порог t.
Теперь, нам нужно на основе величин сформировать единый критерий (одно число), по которому мы бы судили о качестве разбиения выборки на две подвыборки. Это также можно выполнить различными способами, но часто используется следующая формула под названием информационный выигрыш (information gain):
где 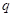
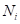
Если посчитать этот критерий для других порогов t, то окажется, что при t = 12 имеем наибольшее значение. А, значит, наилучшее разбиение с точки зрения выбранных критериев: энтропии и информационного выигрыша.
Математически поиск наилучшего предиката в текущей вершине дерева, можно записать так:
Или, в общем случае, учитывая, что мы подбираем не только пороги, но и признаки , по которым делятся объекты на две подвыборки, имеем:
А в качестве impurity, помимо энтропии также используют:
- критерий Джини (Gini impurity):
, здесь
— вероятность (частота) появления объектов k-го класса в вершине дерева;
- ошибка классификации (misclassification error):
.
(Критерий Джини не следует путать с индексом Джини, о котором мы ранее говорили – это две совершенно разные характеристики.) На практике критерий Джини работает почти также, как и энтропия. Это хорошо видно из графиков данных критериев при бинарной классификации: 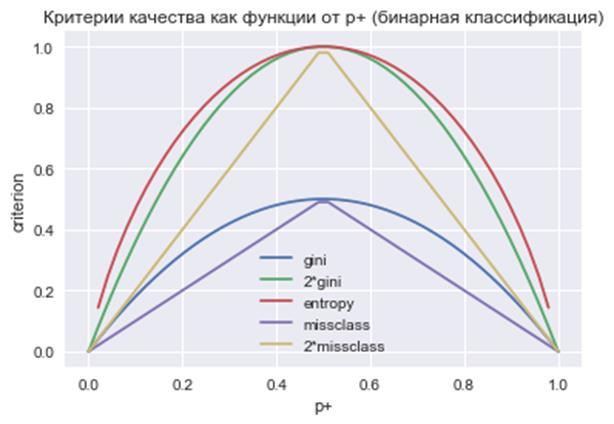
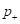
Источник
Какие критерии информативности используются при синтезе решающего дерева и почему?
Дерево решений — это контролируемый алгоритм обучения, используемый как для задач классификации, так и для задач регрессии. Проще говоря, он принимает форму дерева с ветвями, представляющими возможные ответы на заданный вопрос. Существуют метрики, используемые для обучения деревьев решений. Одним из них является получение информации
Можно определить прирост информации как меру того, сколько информации предоставляет функция о классе. Получение информации помогает определить порядок атрибутов в узлах дерева решений. Главный узел называется родительским узлом, тогда как подузлы называются дочерними узлами. Мы можем использовать прирост информации, чтобы определить, насколько хорошо разделение узлов в дереве решений. Это может помочь определить качество расщепления.Расчет прироста информации поможет лучше понять эту концепцию.
Термин Gain — «выигрыш» означает прирост информации. Eparent — это энтропия родительского узла, а E_
Чем больше удалено энтропии, тем больше прирост информации. Чем выше прирост информации, тем лучше разделение. В качестве родительского (корневого) узла следует выбрать атрибут с наибольшим информационным приростом из набора.
Создавайте дочерние узлы для каждого значения атрибута A, следуя тому же принципу. Повторяйте итеративно, пока не закончите построение всего дерева.
Источник
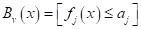
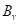
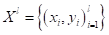

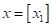
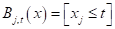
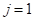
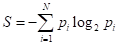
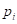
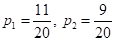
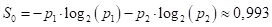
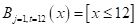
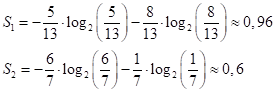
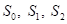
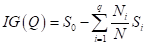
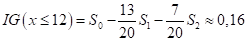
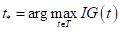
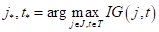
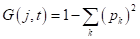 , здесь
, здесь 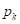 — вероятность (частота) появления объектов k-го класса в вершине дерева;
— вероятность (частота) появления объектов k-го класса в вершине дерева;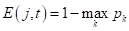 .
.