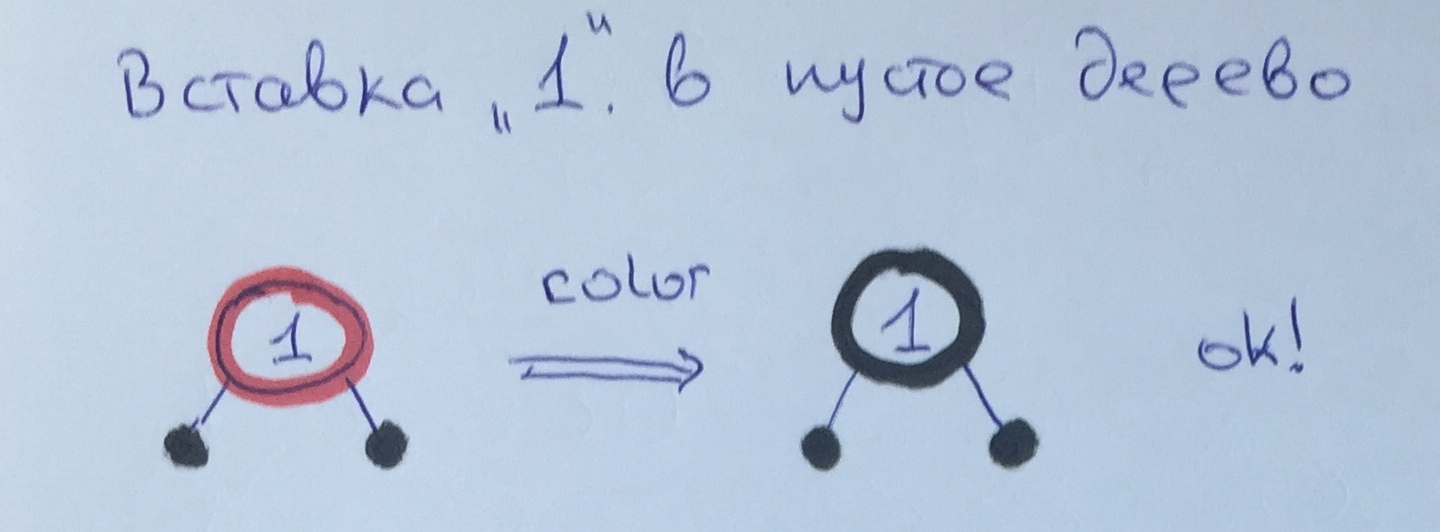Левый поворот красно черного дерева

30. Красно – черные деревья. Свойства. Вращение. Высота красно – черного дерева.

Красно-черные деревья пред­ставляют собой одну из множества «сбалансированных» схем деревьев поиска, ко­торые гарантируют время выполнения операций над динамическим множеством O(log₂n) даже в наихудшем случае.

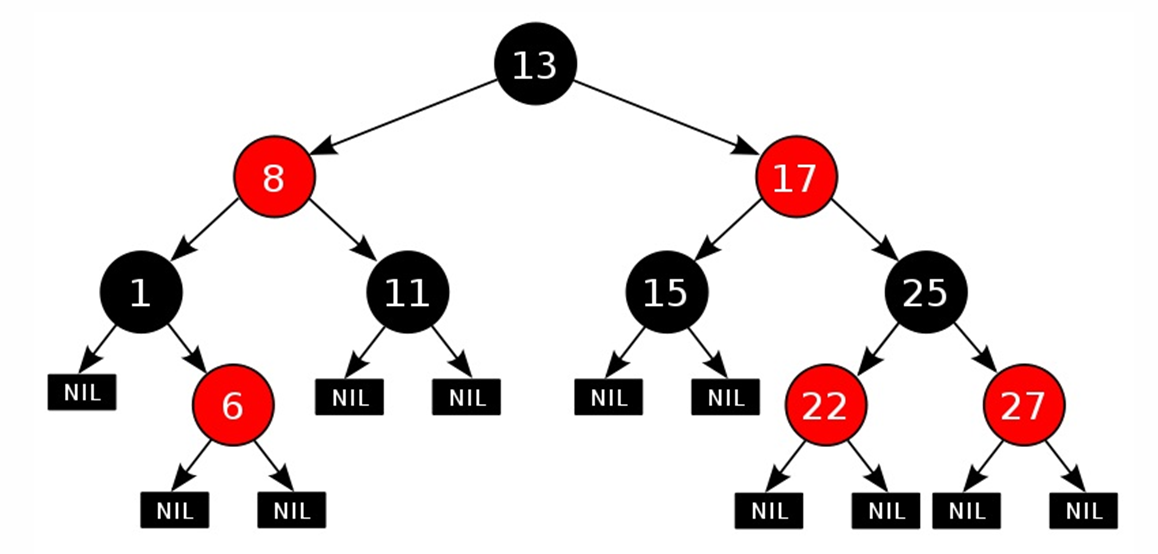
Красно-черное дерево (red-black tree) — это двоичное дерево поиска, вершины которого разделены на красные (red) и черные (black). Таким образом каждая вершина хранит один дополнительный бит — её цвет.

При этом выполняются определённые требования, которые гарантируют, что глубины любых двух листьев отличаются не более чем в два раза.

Каждая вершина красно-черного дерева имеет поля color (цвет), key (ключ), left (левый ребенок), right (правый ребенок) и p (родитель). Если у вершины отсутствует ребенок или родитель, то соответствующее поле содержит NIL.

Двоичное дерево поиска называется красно-черным, если оно обладает следующими свойствами:

1. каждая вершина — либо черная, либо красная ;
2. корень дерева является черным;
3. каждый лист (NIL) — чёрный ;
4. если вершина красная, оба её ребенка чёрные ;
5. все пути, идущие вниз от корня к листьям, содержат одинаковое количество чёрных вершин.

Повороты

Операции над деревом поиска Tree_Insert и Tree_Delete, будучи приме­нены к красно-черному дереву с n ключами, выполняются за время O(log₂n). Поскольку они изменяют дерево, в результате их работы могут нарушаться крас­но-черные свойства. Для восстановления этих свойств мы должны изменить цвета некоторых узлов дерева, а также структу­ру его указателей. Изменения в структуре указателей будут выполняться при помощи поворотов (rotations), которые представляют собой локальные операции в дереве поиска, сохраняющие свойство бинарного дерева поиска. На рис. показаны два типа поворотов — левый и правый (здесь — произвольные поддеревья). При выполнении левого поворота в узлех предполагается, что его правый дочерний узел у не является листом nil [T]. Левый поворот выполняется «вокруг» связи между х и у, делая у новым корнем поддерева, левым дочерним узлом которого становится х, а бывший левый потомок узла у — правым потомком х.

Операции поворота в бинарном дереве поиска

В псевдокоде процедуры Left_Rotate предполагается, что right[х] nil [Т], а родитель корневого узла — nil[T]. Left_Rotate(T, х)

1. у right[x] Устанавливаем у.
2. right[x] left[y] Левое поддерево у становится правым поддеревом х

3 if left[y]nil[T] 4 then p[left[y]] х

1. р[у]р[х] Перенос родителя х в у
2. if p[x] = nil[T]

1. then root[T]у
2. else if x = left[p[х]]

9 then left [p[x]] у 10 else right[p[x]] у

1. left[y] xx— левый дочерний у
2. p[x]у

31. Добавление вершины в красно – черном дереве.

Сначала выполняется обычная операция включения в двоичное дерево Tree_Insert и новая вершина помечается красным цветом. После этого восстанавливаются RB-свойства, если они нарушены путем перекраски вершин и вращений. Рассмотрим случаи нарушения RB-свойств на примере включения в дерево: При включении х нарушено третьеRB-свойство для вершины 5 (оба сына должны быть черные). Т.е. RB-свойство нарушается, если родитель нового узла красный. Как можно восстановить его: Случай 1: Если родитель красный, то родитель родителя – черный (в силу RB-свойства 2). Если у деда (7) второй сын – у ( дядя нового узла х) тоже красный, то можно перекрасить указанных предков: сделать деда красным, а родителя и дядю – черными. Это не изменит черную высоту дерева и восстановит третье свойство для родителя(5). После перекраски. Т.е. теперь 5 – черная вершина, которая может иметь и красного и черного сына. Но появился новый красный узел х(7). Теперь нарушено 3-еRB-свойство родителя узла 7 (2), т.к. этот узел тоже красный. К сожалению дядя (14) не красный и перекраску делать нельзя, не нарушив черной высоты. Тогда используем LL – поворот родителя х – (2). Исправлено нарушение 3-го свойства для узла 2, но нарушено для узла 7. Случай 3 отличается от случая 2 тем, что х является левым, а не правым сыном своего родителя. В этом случае делаем правый поворот родителя (11). Красную вершину 7, оказавшуюся в корне, окрашиваем в черную, а вершины 2 и 11 – в красные. Это не нарушит RB-свойство 4). RB_Insert (T, x)

1. Tree_Insert (T, x)
2. color [x] ← RED
3. while x ≠ root [T] and color [p[x]] = RED
4. dv if p[x] = left [p[p[x]]]
5. then y ← right [p[p[x]]]
6. if color [y] = RED
7. then color [p[x]] ← BLACK случай 1
8. color [y] ← BLACK случай 1
9. color [p[p[x]]] ← RED случай 1
10. x ← p[p[x]] случай 1
11. else if x = right [p[x]]
12. then x ← p[x] случай 2
13. Left_Rotate (T, x) случай 2
14. color [p[x]] ← BLACK случай 3
15. color [p[p[x]]] ← RED случай 3
16. Right_Rotate (T, p[p[x]]) случай 3
17. else (симметричный текст с заменой left ↔ right)
18. color [root[T]] ← BLACK

При включении, если выпадает случай 3, выполняется не более одного вращения, и в случае 2 – не более двух вращений.

Источник

Балансировка красно-чёрных деревьев — Три случая

Двоичные деревья поиска — эта структура данных для хранения элементов с возможностью быстрого поиска. Идея проста и гениальна: «меньше – налево, больше – направо». На этом простота заканчивается и начинаются сложные вопросы балансировки дерева, чтобы оно не превратилось в длинную ветку.

В этой статье мы дадим определение, перечислим правила размещения элементов в красно-чёрном дереве, рассмотрим алгоритм балансировки и закрепим сказанное на примере. Более подробно эту тему, а также другие виды двоичных деревьев поиска мы изучаем на курсе «Алгоритмы для разработчиков».

Красно-чёрное дерево — самобалансирующиеся двоичное дерево поиска, которое гарантирует логарифмический рост высоты дерева от числа узлов и быстрое выполнение основных операций дерева поиска: добавление, удаление и поиск узла.

Красно-чёрное дерево не является полностью сбалансированным, в некоторых местах его высота может различаться почти в два раза. Такое допущение ассимптотически не влияет на скорость поиска элементов, но значительно ускоряет размещение новых элементов, потому что не нужно каждый раз при добавлении элементов «сильно трясти» дерево, иной раз достаточно просто добавить красный элемент, не трогая остальные и не изменяя «чёрную высоту».

Правила размещения элементов в красно-чёрном дереве

1. Каждый узел либо красный, либо чёрный, NIL-листья всегда чёрные.
2. Корень дерева всегда чёрный
3. Оба потомка каждого красного узла — чёрные
4. Путь вниз от любого узла до любого листа-потомка содержит одинаковое число чёрных узлов.

Рассмотрим правила балансировки для выполнения 3 и 4 пункта.
На каждом рисунке предполагается, что мы уже добавили элемент Х, который нарушает 3 правило, нужно так изменить структуру дерева, чтобы 3 правило выполнялось, а 4 не нарушилось.

Условные обозначения вершин:

• X — добавленный элемент, который нарушает 3 пункт правил.
• P — папа элемента Х
• G — дедушка элемента Х, папа элемента Р
• U — дядя элемента Х, брат элемента Р, второй сын элемента G.

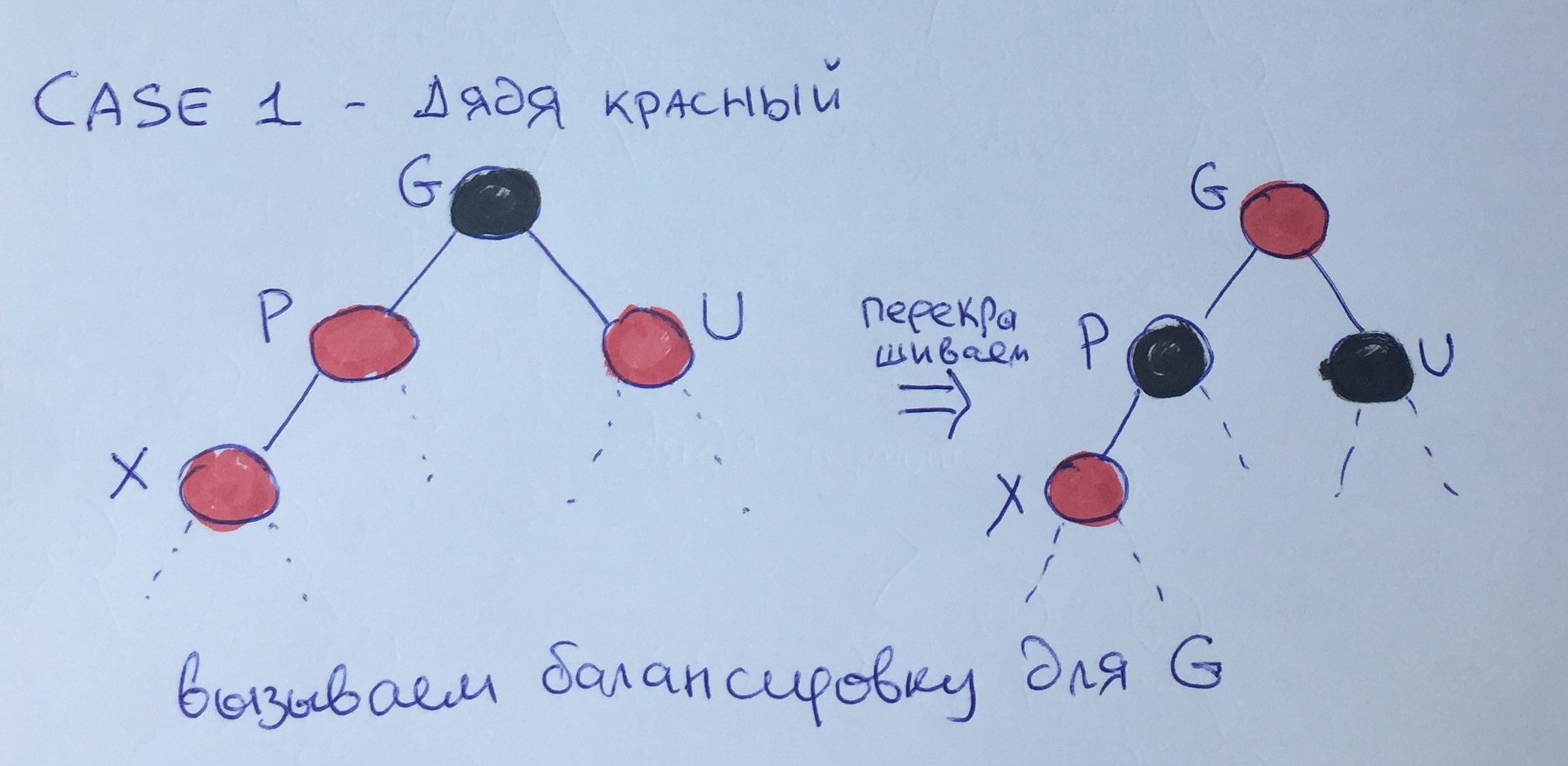
Случай первый — красный дядя

Если и отец, и дядя красного цвета, то мы можем «спустить» чёрный цвет с уровня деда на уровень отца и перекрасить узлы, как показано на рисунке. В этом случае «чёрная высота» останется прежней, однако возможно нарушение 3 правила для элемента G, поэтому необходимо рекурсивно вызвать дальнейшую балансировку для этого узла.

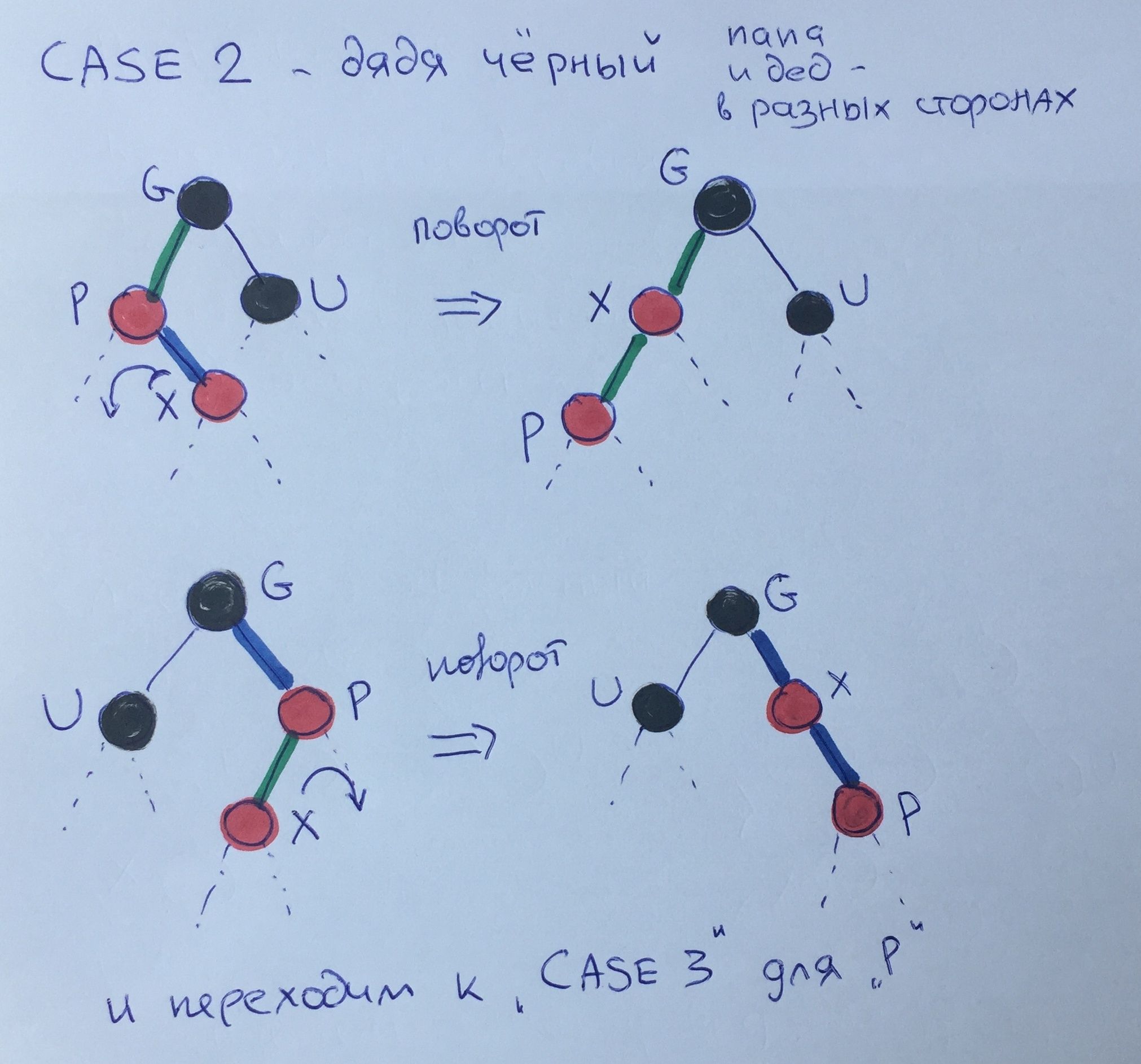
Случай второй — чёрный дядя — папа и дед в разных сторонах.

Эту структуру необходимо привести к третьему случаю, когда папа и дед идут в одну сторону. Для этого нужно выполнить малый поворот от сына Х к его отцу (правила поворотов в этой статье не рассматриваются) и вызвать 3 случай для элемента Р.

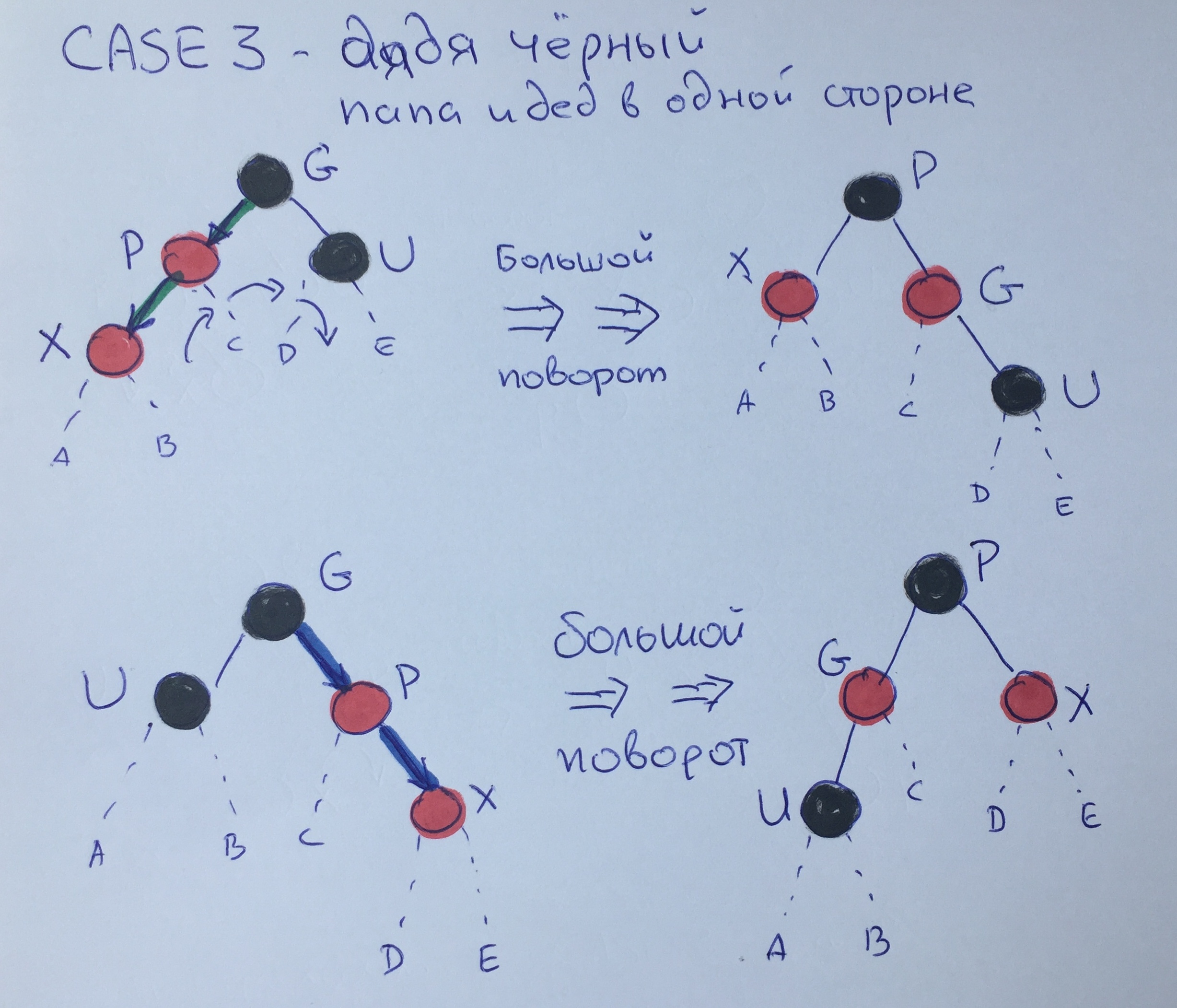
Случай третий — чёрный дядя — папа и дед в одной стороне

В этом случае мы уже можем совершить большой поворот от отца через деда к чёрному дяде и перекрасить Р в чёрный, а G в красный. В результате этого поворота 3-правило будет выполнено.

Убедимся, что 4 правило тоже выполняется. Предположим, что до большого поворота чёрная высота элемента G была N+2. Тогда высота «подвешенных» элементов будет следующей:

A = N+1,
B = N+1,
C = N+1,
D = N,
E = N.

Убедитесь сами, что после поворота 4-правило выполняется для всех элементов.

Конкретный пример

Теперь рассмотрим процесс формирования красно-чёрного дерева при последовательной вставке элементов 1, 2, 3, 4, 5 и 6.

Так как элемент 1 является корнем — мы его просто перекрашиваем для выполнения 1 правила.

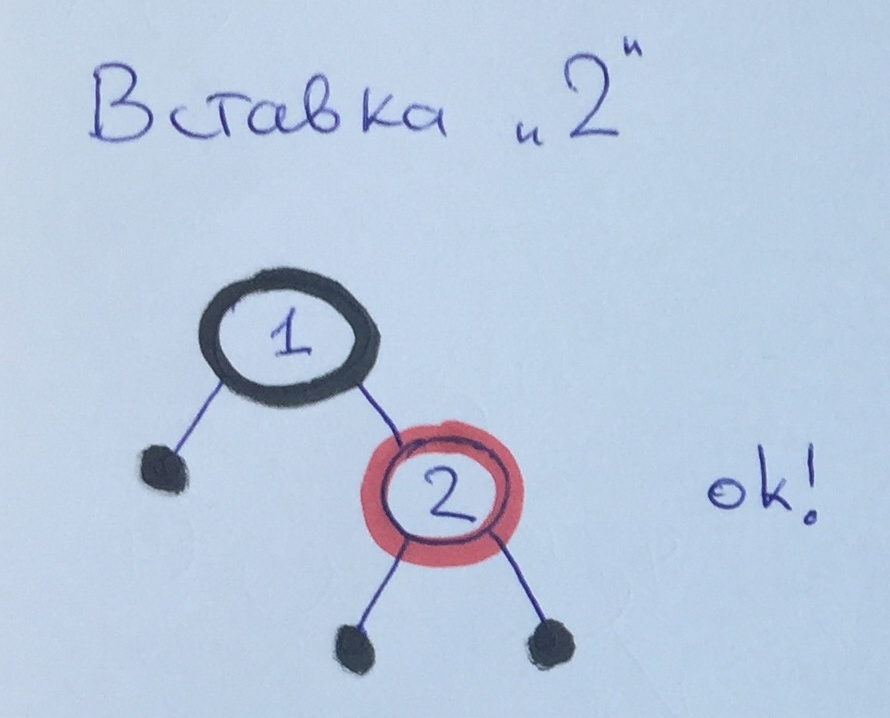
После добавления элемента 2 все правила выполняются.

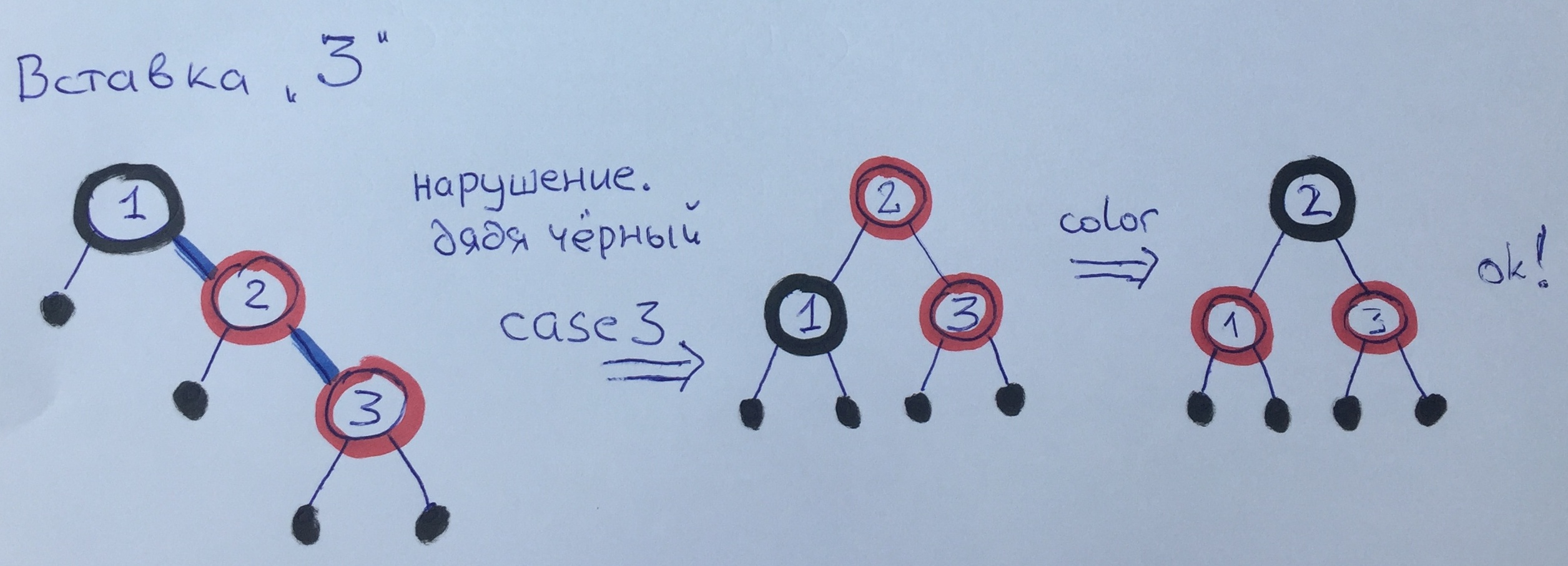
При добавлении элемента 3 у нас нарушилось 3 правило. Так как у нас дядя чёрный, а дед и отец с одной стороны, то мы применяем третий случай — делаем поворот и перекрашиваем.

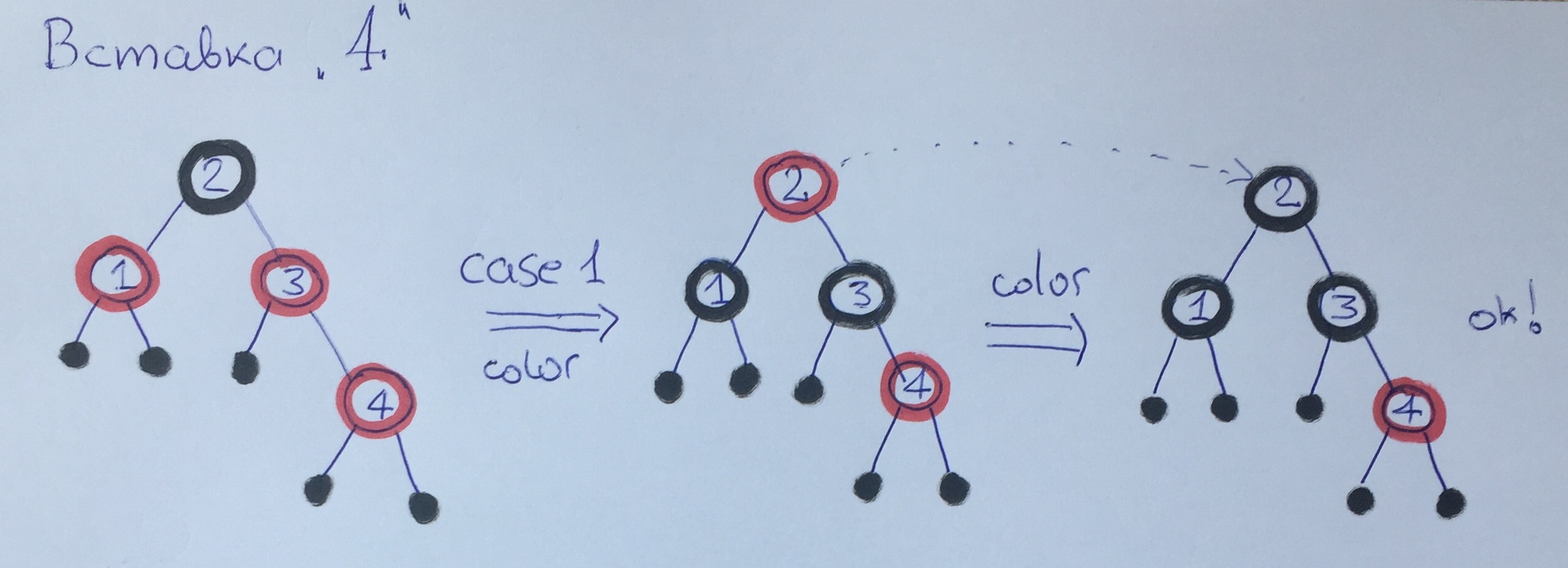
При добавлении элемента 4 у нас опять нарушается 3 правило. На этот раз дядя у нас красный, поэтому применим первый случай с перекрашиванием — чёрная высота дерева увеличится на 1. Обратите внимание. что алгоритм балансировки запускается ещё дополнительно для деда — элемента 2, который, как корень, просто перекрашивается в чёрный цвет.

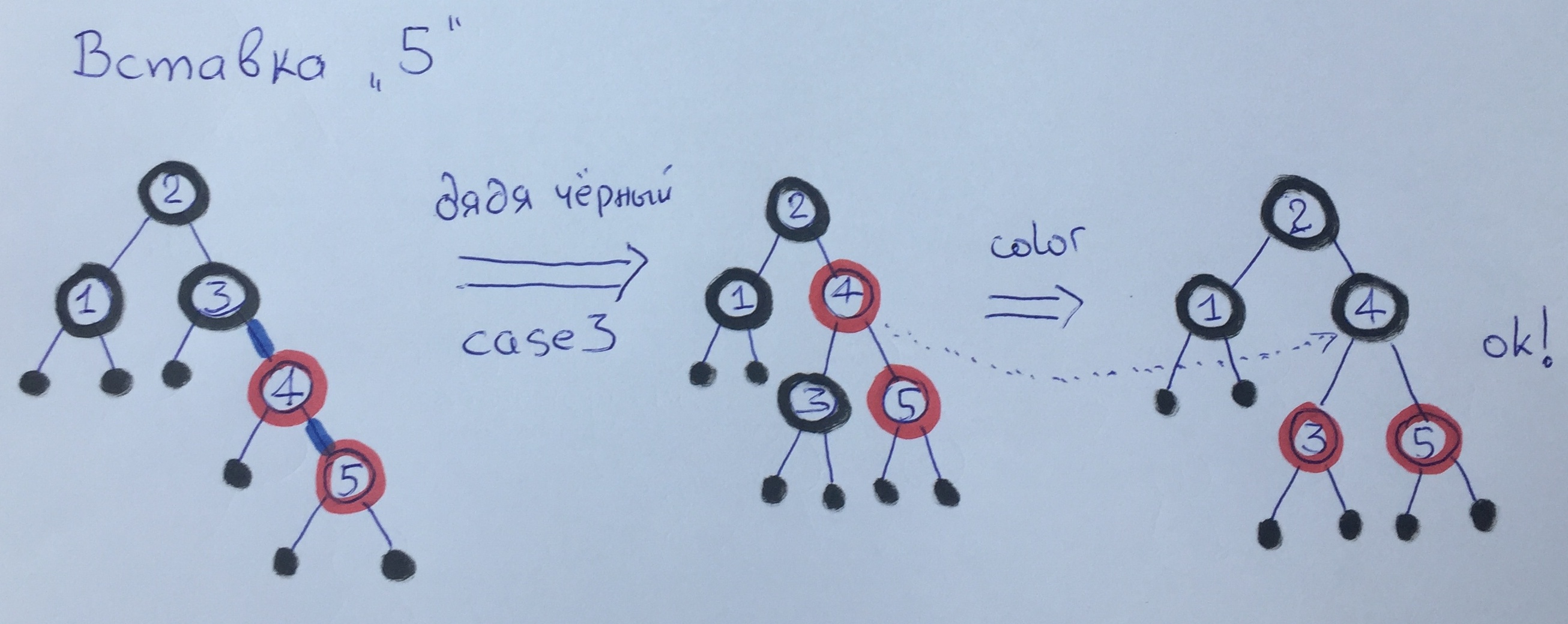
При вставке элемента 5 мы снова применяем 3 случай — делаем большой поворот и перекрашиваем вершины. Обратите внимание, что чёрная высота не изменилась.

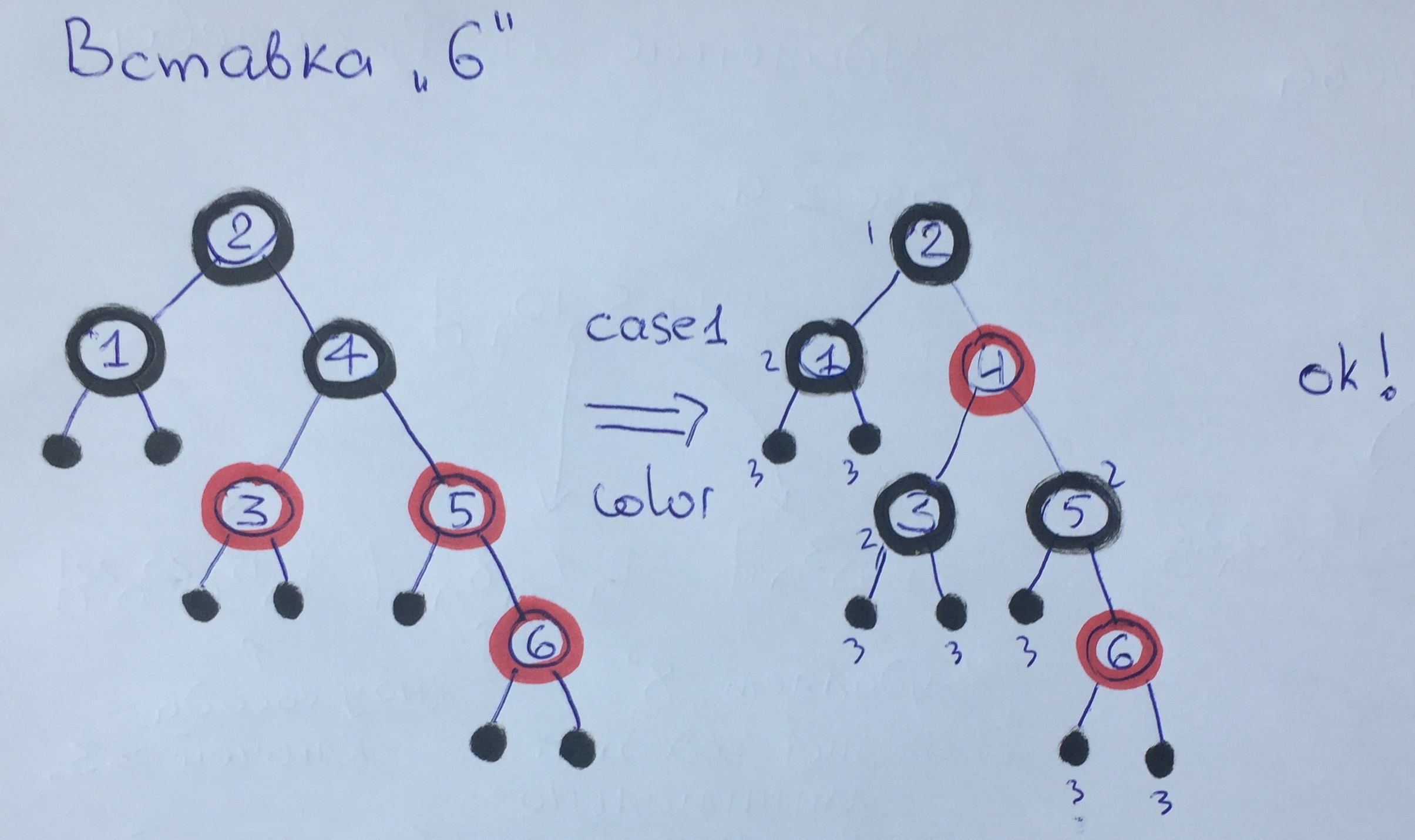
При добавлении элемента 6 мы снова нарушили 3 правило. Так как наш дядя красный, то применяем первый случай с перекрашиванием, чёрная высота не изменилась. Вызов балансировки для 4 элемента ничего не изменило в дереве, так как этот элемент не нарушает правил.

Итак, мы познакомились с вопросами балансировки красно-чёрного дерева, более подробно и с примерами алгоритмов эту тему, а также разновидности других двоичных деревьев поиска мы рассматриваем на курсе «Алгоритмы для разработчиков».

Источник