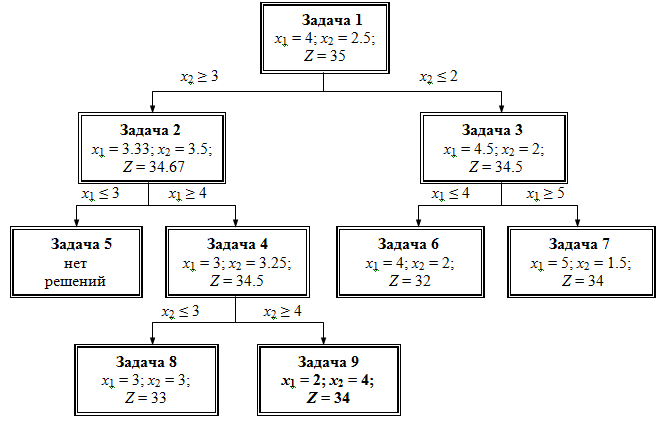
2. Метод построения дерева решений
Еще один вариант использования ситуационного анализа для прогнозирования возможных действий имеет более общее применение и основан на оценках риска.
Принятие решений экономического характера может осуществляться в одной из следующих четырех ситуаций: в условиях определенности, риска неопределенности и конфликта. Первая ситуация имеет место в том случае, если можно с приемлемой точностью предсказать однозначно трактуемые последствия принятого решения. В условиях риска поле возможных исходов, т.е. последствий принятого решения, вариабельно, однако значения исходов и вероятности их появления поддаются количественной оценке. В условиях неопределенности подобной оценки сделать уже нельзя, т.е. не могут быть перечислены все возможные исходы и/или заданы их вероятности. В условиях конфликта принятие решения осложняется не только и не столько возможностью проявления действия некоторых случайных факторов, сколько необходимостью учета безусловного, осознанного и активного противодействия участников «конфликтной» ситуации 1 , причем число этих участников, их информационные и другие ресурсы и возможности могут быть заранее не известны.
Первая ситуация достаточно редка, а ее описание и алгоритмизация не представляют сложности (например, решение принимается на основе некоторого критерия, исчисленного так называемым «прямым счетом» по исходным данным: таким критерием может быть заданная величина прибыли, расходов, рентабельности и др.
В условиях действия второй ситуации для выбора варианта действий и применяется вероятностный подход, предполагающий прогнозирование возможных исходов и присвоение им вероятностей. При этом пользуются:
а.) известными, типовыми ситуациями (типа — вероятность появления герба при бросании монеты равна 0.5);
б) предыдущими распределениями вероятностей (например, из выборочных обследований или статистики предшествующих периодов известна вероятность появления бракованной детали, относительная величина сомнительного долга и др.):
в) субъективными оценками, сделанными аналитиком самостоятельно либо с привлечением группы экспертов.
3. Линейное программирование
Метод линейного программирования, наиболее распространенный в прикладных экономических исследованиях ввиду его достаточно наглядной интерпретации, позволяет хозяйствующему субъекту дать обоснование наилучшему (по формальным признакам) решению в условиях более или менее жестких ограничений относительно доступных для предприятия ресурсов. С помощью линейного программирования в анализе финансово-хозяйственной деятельности решается ряд задач, в первую очередь относящихся к процессу планирования деятельности — он позволяет отыскивать оптимальные параметры выпуска и способы наилучшего использования имеющихся ресурсов.
Суть метода линейного программирования заключается в поиске максимума или минимума выбранной в соответствии с интересами аналитика целевой функции при имеющихся ограничениях. Примеры использования данного метода и технику расчетов можно найти в монографической и учебной литературе (см. например, [Ковалев, Волкова]).
На практике метод линейного программирования нашел применение в системах управленческого учета и внутреннего анализа, в частности при решении задачи оптимизации производственной программы (выбор программы действий при наличии ограничений на затраты сырья, величину спроса и т.п.) и транспортной задачи (оптимизация доставки продукции при наличии сети поставщиков и получателей в условиях ограничений на ресурсы различного вида).
Источник
Метод ветвей и границ
Инструкция . Укажите количество переменных и число ограничений. Полученное решение сохраняется в формате MS Word с проверкой решения в MS Excel . При этом ограничения типа xi ≥ 0 не учитывайте.
Суть метода ветвей и границ состоит в последовательном переборе вариантов, рассмотрении лишь тех из них, которые по определенным признакам оказываются перспективными, и отбрасывании бесперспективных вариантов. При использовании метода ветвей и границ область допустимых решений (ОДР) исходной задачи определенным способом разбивается на непересекающиеся подмножества, и решаются подзадачи, т.е. задачи на этих подмножествах с той же ЦФ и без учета условия целочисленности (как задачи ЛП). Если в результате получено оптимальное нецелочисленное решение, ОДР подзадачи снова разбивается на части и этот процесс продолжается до тех пор, пока не будет найдено оптимальное целочисленное решение исходной задачи.
Если в задаче на максимум при решении подзадач получаются оптимальные целочисленные решения, то запоминаются те из них, которым соответствуют возрастающие значения ЦФ. Если полученное «непрерывное» решение подзадачи оказывается не лучше сохраненного целочисленного решения, то такая подзадача исключается из списка задач. Название этого метода объясняется тем, что в процессе решения задача последовательно «ветвится», разбиваясь на более простые подзадачи.
Примечание: метод ветвей и границ используется также и в задаче коммивояжера.
Пример №1 . В задаче методом Гомори (или методом ветвей и границ) найти оптимальные решения задач целочисленного линейного программирования. Дать геометрическую интерпретацию процесса решений задач.
Z=3x1 + 2x2 → max
при ограничениях:
x1 + x2 ≤ 13
x1 — x2 ≤ 6
-3x1 + x2 ≤ 9
x1≥0, x2 ≥0
x1, x2 – целые числа.
Пример №2 .
5x1 + 2x2 ≤ 14
2x1 + 5x2 ≤ 16
x1 , x2 – целые числа
Z = 3x1 + 5x2 → max
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
Оптимальное значение переменной x1=1.81 оказалось нецелочисленным.
Разбиваем задачу 1 на две подзадачи 11 и 12.
В первой из них к условиям задачи 11 добавляется условие х1 ≥ 2, а к задаче 12 — условие х1 ≤ 1.
Эта процедура называется ветвлением по переменной х1.
Решим графически задачу 11 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x1≥2 (3)
x1≥0 (4)
x2≥0 (5)
Область допустимых решений представляет собой треугольник.
Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
5x1+2x2≤14
x1≥2
Решив систему уравнений, получим: x1 = 2, x2 = 2
Откуда найдем максимальное значение целевой функции:
F(X) = 3*2 + 5*2 = 16
Решение задачи получилось целочисленным.
Новое значение текущего рекорда будет равно F(X) = 16.
Так как найденная точка является первым целочисленным решением, то ее и соответствующее ей значение ЦФ следует запомнить. Сама точка называется текущим целочисленным рекордом или просто рекордом, а оптимальное значение целочисленной задачи — текущим значением рекорда. Это значение является нижней границей оптимального значения исходной задачи Z*.
Область допустимых решений представляет собой многоугольник
Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
2x1+5x2≤16
x1≤1
Решив систему уравнений, получим: x1 = 1, x2 = 2.8
Откуда найдем максимальное значение целевой функции:
F(X) = 3*1 + 5*2.8 = 17
Оптимальное значение переменной x2=2.8 оказалось нецелочисленным.
Разбиваем задачу 12 на две подзадачи 121 и 122.
В первой из них к условиям задачи 121 добавляется условие х2 ≥ 3, а к задаче 122 — условие х2 ≤ 2.
Текущий рекорд Z=16≥13, поэтому прекращаем ветвление из этой вершины
Оптимальное значение переменной x1=0.5 оказалось нецелочисленным.
Разбиваем задачу 121 на две подзадачи 1211 и 1212.
В первой из них к условиям задачи 1211 добавляется условие х1 ≥ 1, а к задаче 1212 — условие х1 = 0.
Текущий рекорд Z=16≥16, поэтому прекращаем ветвление из этой вершины
Оптимальное значение переменной x2=2.48 оказалось нецелочисленным. Разбиваем задачу 1 на две подзадачи 11 и 12.
В первой из них к условиям задачи 11 добавляется условие х2 ≥ 3, а к задаче 12 — условие х2 ≤ 2.
Эта процедура называется ветвлением по переменной х2.
Текущий рекорд Z=16≥16, поэтому прекращаем ветвление из этой вершины
Оптимальное значение переменной x1=0.5 оказалось нецелочисленным. Разбиваем задачу 11 на две подзадачи 111 и 112. В первой из них к условиям задачи 111 добавляется условие х1 ≥ 1, а к задаче 112 — условие х1 = 0.
Решим графически задачу 111 как задачу ЛП.
5x1+2x2≤14 (1)
2x1+5x2≤16 (2)
x2≥3 (3)
x1≥1 (4)
x1≥0 (5)
x2≥0 (6) Задача не имеет допустимых решений. ОДР представляет собой пустое множество
Источник