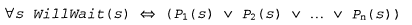Логический вывод деревьев решения

3. Преобразование дерева решений в правила

Как уже говорилось, правило «ЕСЛИ-ТО» состоит из двух частей. Часть ЕСЛИ может включать несколько условий, которые связываются между собой логическими операторами И, ИЛИ и НЕ. Часть ТО правила включается в работу только в том случае, если истинны все условия в условной части. В дереве решений обеим частям правила соответствуют связанные между собой вершина(ы) логического условия(ий) (кружки) и вершина логического вывода (прямоугольник). Условная часть содержит все вершины условия, находящиеся на пути к логическому выводу, т.е. каждая вершина решения на пути к выводу — это одно условие части ЕСЛИ, например, вершины 1 и 4. Вывод же составляет часть ТО правила, в данном примере вершина 6.

Процесс формирования правил для всех возможных логических выводов состоит из следующих шагов:

1. Выбрать из дерева решений вершину вывода (прямоугольник) и зафиксировать её.
2. В обратном направлении линии (стрелки) найти вершину условия (кружок) и зафиксировать её.
3. Повторять шаг 2 до тех пор, пока не будут исчерпаны все вершины условия, расположенные в обратном направлении стрелок от зафиксированной вершины вывода, или не встретится вершина локального вывода. Если встретилась вершина локального вывода, то её надо зафиксировать и прекратить выполнение шага 2.
4. Каждая вершина условия (кружок), составляющая путь, — это одна из переменных части ЕСЛИ правила. Эти вершины объединяются логическим оператором И.
5. Выбранный на шаге 1 логический вывод перенести в часть ТО правила.

Пример создание правила. В качестве примера рассмотрим путь 6, 4, 5, 3. Создание правила начинается с вывода (вершина 6) и дерево решения просматривается в обратную сторону. Просмотр данной ветви (пути) заканчивается на вершине 3, которая является локальным выводом. Если бы вершины 3 не было в дереве решений, то путь закончился бы на вершине 1.

Применив полученный путь, запишем правило в следующем виде:

ЕСЛИ посетитель, возможно, будет принят на работу = да

И средний балл за время учебы >=3,5

И посетитель имеет изобретения = да,

ТО предложенная должность = научный сотрудник.

Для каждой вершины логического вывода определяется путь и записывается правило. В рассматриваемом дереве решений имеется 6 вершин логического вывода (прямоугольников), в том числе и локальный вывод в вершине 3, значит будет составлено 6 правил.

Длинную фразу “посетитель, возможно, будет принят на работу ” можно заменить переменной, принимающей значения “да” или “нет”. В действительности все вершины содержат переменные, имеющие уникальные имена. Список имен переменных, текст, который они заменяют, и номера вершин пути сводят в таблицу, (табл. 6.1). Использование переменных вместо полного текста упрощает формирование и запись правил.

Источник

28. Деревья принятия решений.

Индуктивный логический вывод деревьев решений представляет собой одну из простейших и вместе с тем наиболее успешных форм алгоритмов обучения. Дерево решений принимает в качестве входных данных объект или ситуацию, описанную с помощью множества атрибутов, и возвращает “решение” — пред­сказанное выходное значение, соответствующее входным данным. Входные атрибу­ты могут быть дискретными или непрерывными. Выходные значения также могут быть дискретными или непрерывными; процесс формирования в ходе обучения функции с дискретными значениями называется обучением классификации; формирование в ходе обучения непрерывной функции называется обучением регрессии. Вначале мы сосредоточимся на булевой классификации, согласно ко­торой каждый пример обозначается как истинный (положительный) или ложный (отрицательный).

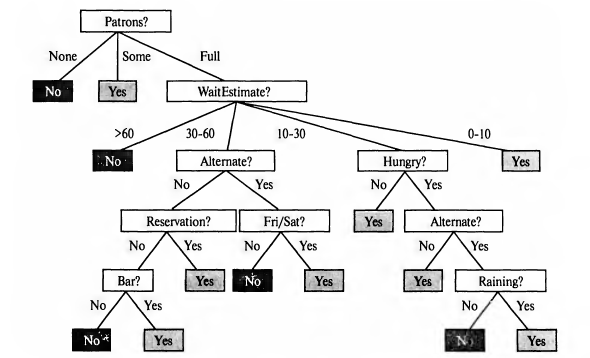
Дерево решений позволяет перейти к содержащемуся в нем решению путем вы­полнения последовательности проверок. Каждый внутренний узел в дереве соответ­ствует проверке значения одного из свойств, а ветви, исходящие из этого узла, обо­значены возможными значениями результатов проверки. Каждый листовой узел в дереве задает значение, возвращаемое после достижения этого листа.

Например: клиент ждет, пока освободится место за столиком в ресторане. Цель состоит в том, чтобы изучить определение для целевого предиката WillWait (Следует ли ждать). Используем следующие атрибуты:

• AIternate (Альтернативный вариант). Есть ли поблизости подходящий рес­торан такого же класса.
• Ваr (Бар). Имеется ли в ресторане уютный бар, в котором можно подождать.
• Fri/Sat (Уик-энд). Принимает истинное значение по пятницам и субботам.
• Hungry (Чувство голода). Испытывает ли посетитель чувство голода.
• Patrons (Посетители). Сколько людей находится в ресторане; значениями этого атрибута являются None (Ресторан пуст), Some (В ресторане есть посе­тители) иFull (Ресторан заполнен).
• Price (Цены). Ценовая категория ресторана (*, **, ***).
• Raining (Дождь). Идет ли дождь на улице.
• Reservation (Бронирование). Забронировано ли место за посетителем.
• Туре(Тип). Тип ресторана (ресторан с французской (French), итальянской (Italian), тайской (Thai) кухней или ресторан-закусочная (Burger)).
• WaitEstimate (Оценка продолжительности ожидания). Продолжитель­ность ожидания, оценка которой сделана метрдотелем (0-10, 10-30, 30-60, >60 минут).

Выразительность деревьев решений

С точки зрения логики любая конкретная гипотеза из дерева решений для целевого предиката WillWait может рассматриваться как утверждение в следующей форме:

где каждое условие P_i(s) представляет собой конъюнкцию проверок, соответст­вующих пути от корня дерева к листу с положительным результатом. Деревья решений в рамках класса пропозициональных языков являются полно­стью выразительными; это означает, что в виде дерева решений может быть оформ­лена любая булева функция.

Деревья решений вполне подходят для функций одних типов и не подходят для других(для мажоритарной функции,для функции определения четности)

Источник

Построение деревьев решений

Индуктивный логический вывод деревьев решений – одна из простейших и эффективных форм алгоритмов обучения.

Дерево решений принимает в качестве входных данных множество атрибутов, описывающих объект или ситуацию, и возвращает предсказанное выходное значение, соответствующее этим входным данным. Входные атрибуты и выходные значения могут быть дискретными или непрерывными. Будем рассматривать случай булевой классификации, когда каждый пример может быть либо истинный (положительный), либо ложный (отрицательный).

Решение, содержащееся в дереве решений, может быть получено путем выполнения последовательности проверок. В каждом узле дерева проверяется значение одного из свойств, а ветви, исходящие из этого узла, обозначаются возможными значениями результатов проверки. При достижении листового узла возвращается соответствующее ему значение.

Рассмотрим пример применения метода обучения на основе дерева решений к задаче, в которой клиент ждет, пока освободится место за столиком в ресторане. Целевой предикат WillWait (Следует ли ждать). Вначале определим, какие атрибуты доступны для описания примеров ситуаций в данной проблемной области:

Alternate – есть ли поблизости ресторан такого же класса,

Bar – имеется ли в ресторане бар, в котором можно подождать,

Fri/Sat – атрибут истинен по пятницам и субботам,

Hungry – испытывает ли посетитель чувство голода,

Patrons – Full/Some/None – количество людей в ресторане,

Price – */**/*** – ценовая категория ресторана,

Raining – идет ли дождь на улице,

Reservation – забронировано ли за посетителем место,

Type – French/Italian/Thai/Burger – тип кухни в ресторане,

WaitEstimate – 0-10/10-30/30-60/>60 минут – время ожидания.

Возможное дерево решений показано на рис.3. В нем не используются атрибуты Price и Type, что означает, что лицо, принимающее решение, рассматривает их как малозначительные. Обработка примеров ситуаций с помощью этого дерева начинается от корня и проходит по соответствующей ветви до тех пор, пока не будет достигнут какой-то лист. Например, для ситуации, в которой Patrons = Full и WaitEstimate = 0-10 будет получено положительное решение, т.е. следует дождаться освобождения столика.

Лекция 24

Обучение с использованием знаний.

Логическая формулировка задачи обучения

Обучение с использованием знаний

Рассмотрим логические связи между гипотезами, описаниями примеров и классификациями. Пусть Descriptions обозначает коньюнкцию всех описаний примеров в обучающем множестве, а Classifications – коньюнкцию всех классификаций примеров. В таком случае гипотеза, которая позволяет “объяснить результаты наблюдений”, должна удовлетворять следующему свойству:

Hypothesis & Descriptions |= Classifications

Связь такого рода называется ограничением логического следствия, в котором Hypothesis представляет собой “неизвестное”. Например, если дерево решений рассматривается как логическая формула, то дерево решений, совместимое со всеми примерами, удовлетворяет данному уравнению.

Современный подход состоит в том, что должны проектироваться агенты, которые уже что-то знают и пытаются освоить в процессе обучения некоторую дополнительную информацию. Схема, которая показывает, как в процессе обучения с накоплением знаний используется и со временем обогащается запас фоновых знаний, изображена на рис. 4.

Агент может начать свое существование без какого-либо запаса знаний, осуществляя индуктивные выводы в условиях отсутствия знаний. В дальнейшем агент должен использовать свои фоновые знания для все более эффективного обучения. Вопрос заключается в том, как фактически следует использовать знания в обучении.

Рассмотрим общеизвестные примеры обучения на основе фоновых знаний.

1. В первом примере пещерный человек поджаривает на огне ящерицу, насаженную на заостренную палочку. За ним наблюдает и обучается толпа соплеменников, которые до сих пор разогревали пищу над огнем, держа ее голыми руками.

2. Во втором примере путешественник, прибывший в Бразилию, встречает первого в своей жизни бразильца. Услышав от него речь на португальском языке, путешественник делает вывод, что бразильцы говорят на португальском, но узнав, что его собеседника зовут Фернандо, он не делает вывод, что все бразильцы носят это же имя. Аналогичный пример из научной области: когда студент-физик измеряет плотность и проводимость медного образца при определенной температуре, он обобщает эти данные на все предметы из меди. Но измерив массу этого образца, студент не рассматривает гипотезу, что все предметы из меди имеют такую же массу, хотя он может сделать такое обобщение относительно всех монет одинакового достоинства.

3. Следующий пример: студент-медик присутствует на консультации, которую дает пациенту опытный терапевт. После ряда вопросов и ответов специалист сообщает пациенту, чтобы он прошел курс лечения конкретным антибиотиком. Студент-медик делает вывод, что данный антибиотик является эффективным средством лечения при данном конкретном типе инфекции.

В данных примерах использование фоновых знаний обеспечивает гораздо более быстрое обучение по сравнению с тем, чего можно ожидать при использовании метода чисто индуктивного обучения.

Рассмотрим какие ограничения приведенного выше логического следствия применяются в каждом из этих случаев. В таких ограничениях, кроме гипотезы, описаний наблюдаемых примеров и классификации, применяются фоновые знания Backgraund.

В первом примере используется обобщение, получившее название обучения на основе объяснения (EBL – Explanation-Based Learning). Здесь общее правило следует логически из фоновых знаний, которыми обладают пещерные люди:

Hypothesis & Descriptions |= Classifications

Во втором примере априорные знания Backgraund касаются релевантности множества характеристик по отношению к целевому предикату. Эти знания, наряду с результатами наблюдений, позволяют агенту вывести новое, общее правило, которое объясняет результаты наблюдений, следующим образом:

Hypothesis & Descriptions |= Classifications

Backgraund &Descriptions & Classifications |= Hypothesis

Обобщение такого рода называется обучением с учетом релевантности (RBL – Relevance-Based Learning).

В третьем примере для объяснения примеров объединяются фоновые знания и новая гипотеза:

Backgraund & Hypothesis & Descriptions |= Classifications

Как и при чисто индуктивном обучении, алгоритм обучения должен выдвигать гипотезы, которые являются как можно более простыми и совместимыми с данным ограничением. Такие алгоритмы называются алгоритмами индуктивного обучения на основе знаний (KBIL – Knowledge-Based Inductive Learning).

Источник