Массовое обновление дерево отрезков

Несогласованные поддеревья. Реализация массового обновления

Дерево отрезков позволяет осуществлять массовые операции, то есть данная структура позволяет выполнять операции с несколькими подряд идущими элементами. Причем время работы, как и при других запросах, равно [math]O(\log n)[/math] .

Несогласованные поддеревья

Сперва рассмотрим так называемые несогласованные поддеревья.

Пусть дерево отрезков хранит в вершинах результат выполнения операции [math]\oplus[/math] на текущем отрезке, а запрос обновления идет по операции [math]\odot[/math] .

В несогласованном поддереве дерева отрезков в вершинах хранятся не истинные значения сумм (по операции [math]\oplus[/math] ) на отрезках, однако гарантируется, что на запрос они отвечают верно. При этом в корне поддерева, которому соответствует отрезок [math]a_i..a_j[/math] хранится несогласованность [math]d[/math] . Если в вершине хранится истинное значение суммы, то [math]d = \perp[/math] — нейтральный элемент относительно операции [math]\odot[/math] (например 0 для прибавления). Для реализации операция [math]\odot[/math] должна быть ассоциативной, и операции должны удовлетворять свойству дистрибутивности:

1. [math]a \odot (b \odot c) = (a \odot b) \odot c[/math]
2. [math](a \oplus b) \odot c = (a \odot c) \oplus (b \odot c)[/math]

Массовое обновление

Рассмотрим в общем виде реализацию массовой операции на отрезке. Пусть необходимо отвечать на запросы относительно операции [math]\oplus[/math] , а запрос массового обновления идет по операции [math]\odot[/math] .

Для эффективной реализации будем использовать описанную выше структуру — несогласованные поддеревья. В каждой вершине, помимо непосредственно результата выполнения операции [math]\oplus[/math] , храним несогласованность — величина, с которой нужно выполнить операцию [math]\odot[/math] для всех элементов текущего отрезка. Тем самым мы сможем обрабатывать запрос массового обновления на любом подотрезке эффективно, вместо того чтобы изменять все [math]O(N)[/math] значений. Как известно из определения несогласованных поддеревьев, в текущий момент времени не в каждой вершине дерева хранится истинное значение, однако когда мы обращаемся к текущему элементу мы работаем с верными данными. Это обеспечивается «проталкиванием» несогласованности детям (процедура push) при каждом обращений к текущей вершине. При этом после обращения к вершине необходимо пересчитать значение по операции [math]\oplus[/math] , так как значение в детях могло измениться.

Рассмотрим описанные выше операции более подробно. В каждом нижеприведенном псевдокоде в узлах дерева хранятся структуры из четырех полей:

• [math]\mathtt[/math] — левая граница полуинтервала, за который «отвечает» текущая вершина.
• [math]\mathtt[/math] — правая граница этого полуинтервала.
• [math]\mathtt< ans>[/math] — результат на отрезке по операции [math]\oplus[/math] .
• [math]\mathtt< d>[/math] — несогласованность.

push

«Проталкивание» несогласованности детям. Необходимо выполнять как только идет рекурсивный запуск от текущей вершины к её детям. Нужно это для того, чтобы в детях в момент обработки были корректные данные.

void push(int node) < // node - текущая вершина tree[2 * node + 1].d = tree[2 * node + 1].d [math]\odot[/math] tree[node].d; tree[2 * node + 2].d = tree[2 * node + 2].d [math]\odot[/math] tree[node].d; tree[node].d = [math]\perp[/math]; // Нейтральный элемент >

update

Процедура обновления на отрезке. Данная процедура выполняет разбиение текущего отрезка на подотрезки и обновление в них несогласованности. Очень важно выполнить push как только идет рекурсивный вызов от детей, чтобы избежать некорректной обработки в детях. И так как значение в детях могло измениться, то необходимо выполнить обновление ответа по операции [math]\oplus[/math] на текущем отрезке.

void update(int node, int a, int b, T val) < // val - значение, которое поступило в качестве параметра на запрос, a и b - границы запроса l = tree[node].left; r = tree[node].right; if [l, r) [math]\cap [/math] [a, b) == [math] \varnothing[/math] return; if [l, r) [math]\subset [/math] [a, b) tree[node].d = tree[node].d [math]\odot[/math] val; return; push(node); // Обновление детей update(2 * node + 1, a, b, val); update(2 * node + 2, a, b, val); // Пересчет значения на текущем отрезке tree[node].ans = (tree[2 * node + 1].ans [math]\odot[/math] tree[2 * node + 1].d) [math]\oplus[/math] (tree[2 * node + 2].ans [math]\odot[/math] tree[2 * node + 2].d); >

query

Получение ответа по операции [math]\oplus[/math] . Отличие от операции обновления лишь в том, что для каждого отрезка разбиения необходимо не обновить несогласованность, а сложить по операции [math]\oplus[/math] с текущим ответом истинное значение на отрезке (то есть результат сложения по операции [math]\odot[/math] значения в вершине с несогласованностью).

T query(int node, int a, int b) < l = tree[node].left; r = tree[node].right; if [l, r ) [math]\cap[/math] [a, b) == [math] \varnothing[/math] return [math]\perp[/math]; if [l, r) [math]\subset[/math] [a, b) return tree[node].ans [math]\odot[/math] tree[node].d; push(node); T ans = query(node * 2 + 1, a, b) [math]\oplus[/math] query(node * 2 + 2, a, b)); tree[node].ans = (tree[2 * node + 1].ans [math]\odot[/math] tree[2 * node + 1].d) [math]\oplus[/math] (tree[2 * node + 2].ans [math]\odot[/math] tree[2 * node + 2].d); return ans; >

См. также

Источники информации

Источник

Дерево отрезков

Дерево отрезков — структура данных, позволяющая выполнять многие операции с отрезками массива за \(O(\log N)\). Дерево отрезков — универсальная структура данных, для которой можно реализовать неограниченный набор операций (иногда за большую сложность: \(O(\log^2 N)\)). Самая простая версия дерева отрезков позволяет находить сумму или минимум на отрезке, и изменять отдельные элементы.

Построение дерева отрезков

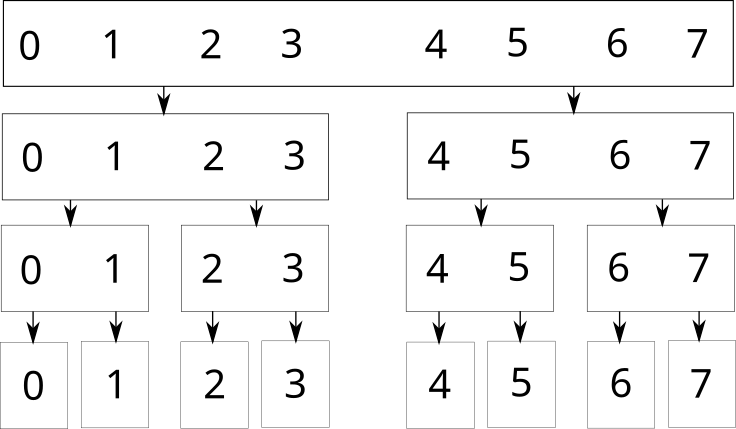
Дерево отрезков — полное бинарное дерево, в котором каждая вершина отвечает за некоторый отрезок в массиве. Корень дерева отвечает за весь массив, его две дочерних вершины — за две половины, и так далее. У каждой вершины, отвечающей за отрезок длиной больше \(1\), есть две дочерних вершины, отвечающих за левую и правую половины этого отрезка. Листья дерева отрезков отвечают за отдельные элементы (отрезки длиной \(1\)).

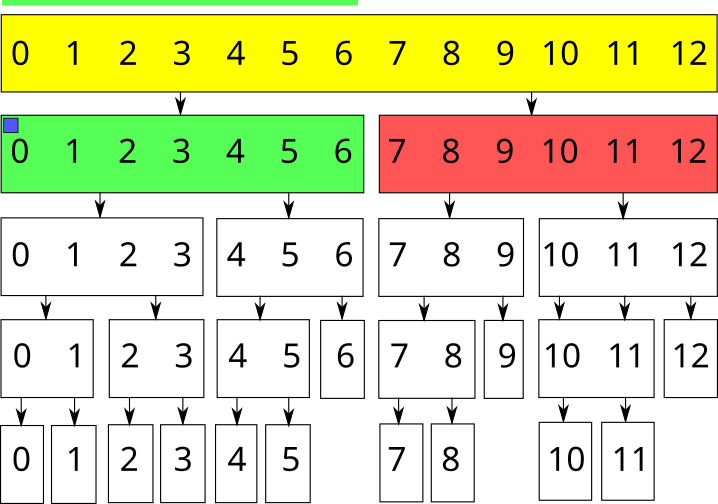
Графически это выглядит следующим образом (для массива из 8 элементов):

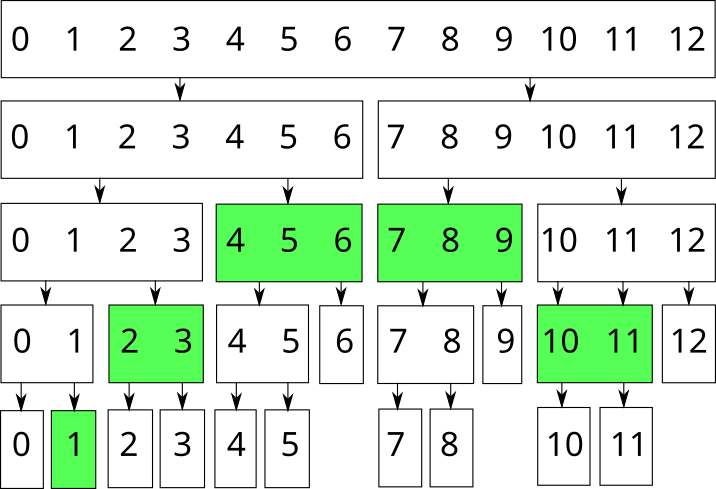
Каждый прямоугольник — вершина дерева отрезков. Если некоторая вершина отвечает за отрезок нечётной длины, то одна из её дочерних вершин будет отвечать за отрезок длиной \(\lceil \rceil\), а другая — за отрезок длиной \(\lfloor \rfloor\). Например, так выглядит дерево отрезков для массива из 13 элементов:

Для массива из \(n\) элементов дерево отрезков имеет около \(2n\) вершин (\(n + + + \ldots\)), а его высота равна порядка \(\log n\).

Главное свойство дерева отрезков, на котором и строятся все алгоритмы работы с ним: любой непрерывный отрезок в массиве из \(n\) элементов можно представить с помощью около \(2 \log n\) вершин в дереве отрезков.

Например, отрезок \([1; 11]\) в массиве длиной \(13\) можно представить с помощью следующих вершин:

Дерево отрезков для поиска суммы

Одна из простейших функций, которую можно считать за \(O(\log N)\) с помощью дерева отрезков — сумма.

При построении дерева в каждой его вершине сохраним сумму на соответствующем отрезке (построение будет вестись рекурсивно, поэтому достаточно просто сложить суммы на двух дочерних отрезках). Затем каждый запрос суммы на отрезке будем разбивать на \(2 \log N\) отрезков, и находить сумму на каждом из них за \(O(1)\), используя предпросчитанные значения. Таким образом сложность запроса суммы равна \(O(\log N)\).

Кроме запросов суммы к дереву отрезков также могут поступать запросы на изменение отдельных элементов (модификацию). Заметим, что от изменения одного элемента значение суммы изменится в одной вершине на каждом уровне дерева отрезков (в которую входит этот элемент). Пересчитаем значения суммы (опять же, рекурсивно) только в этих вершинах. Таким образом сложность запроса модификации равна высоте дерева, или \(O(\log N)\).

Для реализации запроса суммы и запроса модификации обход дерева реализуется с помощью одного и того же алгоритма, основанного на DFS. Пусть границы нашего запроса \([L; R]\) (в случае запроса модификации \(L = R\)), а границы отрезка, соответствующего текущей вершине \([TL; TR]\). В зависимости от взаимного положения этих границ, существуют три варианта действий алгоритма:

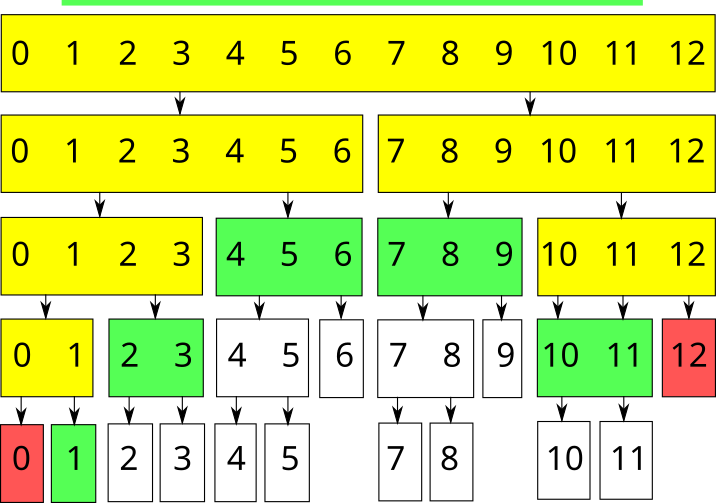
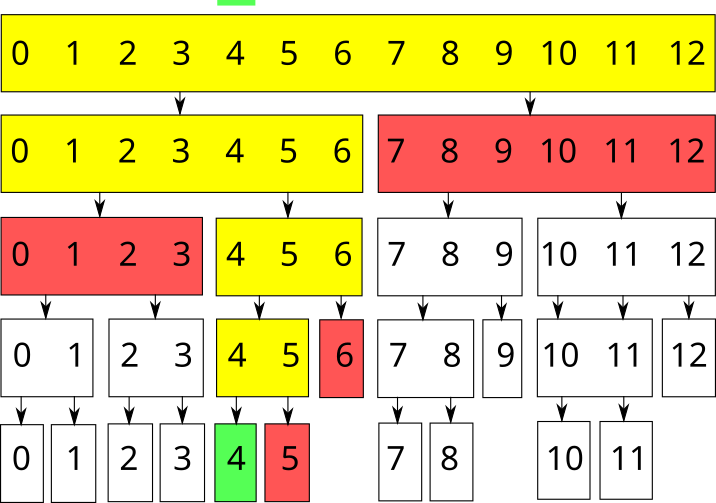
• Текущий отрезок полностью входит в запрос (\(L \le TL; TR \le R\)). Если это запрос суммы, вернём предпросчитанную сумму на отрезке. Если это запрос модификации, изменим элемент и пересчитаем сумму. В дочерние вершины спускаться нет надобности.
• Текущий отрезок полностью не входит в запрос (\(TR < L\) или \(R < TL\)). Никаких действий выполнять не нужно, просто выйдем из функции. Если это запрос суммы, просто вернём \(0\).
• Текущий отрезок частично входит в запрос. Вызовем функцию рекурсивно для двух дочерних отрезков. Если это запрос суммы, вернём сумму двух полученных значений. Если это запрос модификации, пересчитаем значение суммы для текущего отрезка (так как оно могло измениться).

Обозначим эти варианты соответственно зелёным, красным и жёлтым цветом. Тогда запрос суммы на отрезке \([1; 11]\) массива длиной \(13\) будет обработан следующим образом:

А запрос модификации \(4\)-го элемента:

Реализация дерева отрезков для поиска суммы

Полное бинарное дерево представляем, как и, например, кучу, с помощью массива и формул перехода \(l = 2v\) и \(r = 2v + 1\). Для предотвращения всех возможных переполнений размер дерева отрезков для массива из \(n\) элементов принимают равным \(4n\).

brestprog

Источник

Массовое обновление дерево отрезков

pakhomovee → Codeforces Round #893 (Div. 2)

roycf123 → A question on data structures

stdfloat → Groups contain OI problems on Codeforces

Mo7amed_Mohsen → Can’t find my city

-is-this-fft- → Glossary of frequently misused words

ajit → Divide by Zero 2021 and Codeforces Round #714 (Div. 2) Editorial

WH6BNNS → A small suggestion

ssk4988 → How to become a Master

Medeali → Solving Div 1 A in two hours.Is it good for gray coder?

induk_v_tsiane → Codeforces Round #892 (Div. 2) Editorial

induk_v_tsiane → Codeforces Round 892 (Div. 2).

MikeMirzayanov → Изменение правил об использовании стороннего кода в соревнованиях Codeforces

steveonalex → [Tutorial] Divide and Conquer Offline Query — A Niche Way to solve Static Range Query

Shreyash_123 → Sir I have not copied the code from any sources

Vladithur → Codeforces Round #890 (Div. 2) Editorial

__Math_Lover__ → Mojo is Coming and it’s better than C++ AND Python !

BroOnAMission → practice 1600-2000

G eothermal → I’m Geothermal. AMA!

atcoder_official → AtCoder Beginner Contest 314 Announcement

waaitg → Codeforces Round #808 Editorial

_Untrackable_ → div2 892 d

Chess.Master → Interesting problem from ECPC

diskoteka → Codeforces Round #885 (Div.2) Разбор

KitasCraft → I feel like I’m not improving

andrei_iorgulescu → Participating unofficialy no matter your rating

Блог пользователя FairyWinx

Дерево отрезков с массовыми операциями без пушей.

Автор FairyWinx, 2 года назад ,

Решим следующую задачу: Требуется уметь находить произведение чисел на отрезке по модулю, а также умножать все числа на отрезке на некое число x на отрезке. И все по модулю

Понятно, что это решается обычным деревом отрезков с отложенными массовыми операциями. Но в этом случае мы при каждом вызове функции get и update будем пушить значения в детей, что очень долго (У нас в этом случае будет 4 умножения по модулю в функции push). Давайте научимся делать массовые операции не проталкивая значения в детей.

Утверждение, такой код работает (там есть беды с переполнением, но это остается, как упражнение читателю):

void update(int v, int l, int r, int L, int R, int val) < if (R int m = (l + r) / 2; update(v * 2 + 1, l, m, L, R, val); update(v * 2, m, r, L, R, val); t[v] = t[v * 2 + 1] * t[v * 2] * pow(mod[v], (r - l)) % MOD; > 

int get(int v, int l, int r, int L, int R) < if (R 

Почему это так: понятно, что в вершине корректное значение, если мы не смотрим на обновления, которые были сверху. (По аналогии с обычным деревом отрезков). Ну а верхние обновления мы учтем, когда будем спускаться в функции get.

Брать модуль у числа не самое быстрое занятие, поэтому функция push в ДО работает очень долго, и такой способ написания ДО очень сильно ускоряет код (когда я пихал корнячку с таким ДО (ну и там не только операции с ДО были) время с 8 секунд уменьшилось до 6, что очень и очень существенно) Ну и это также работает с минимумом/максимумом/суммой и многими другими функциями, и работает быстрее. Такие вот пироги

Источник