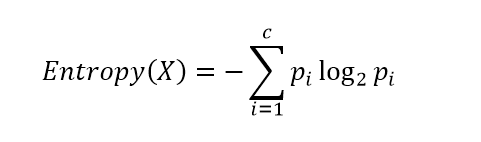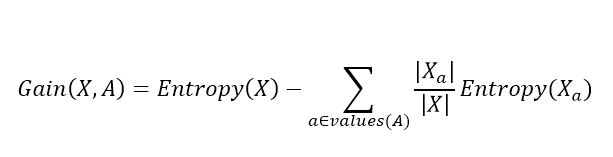9.2. Преимущества деревьев решений
Интуитивность деревьев решений. Классификационная модель, представленная в виде дерева решений, является интуитивной и упрощает понимание решаемой задачи. Результат работы алгоритмов конструирования деревьев решений, в отличие, например, от нейронных сетей, представляющих собой «черные ящики», легко интерпретируется пользователем. Это свойство деревьев решений не только важно при отнесении к определенному классу нового объекта, но и полезно при интерпретации модели классификации в целом. Дерево решений позволяет понять и объяснить, почему конкретный объект относится к тому или иному классу.
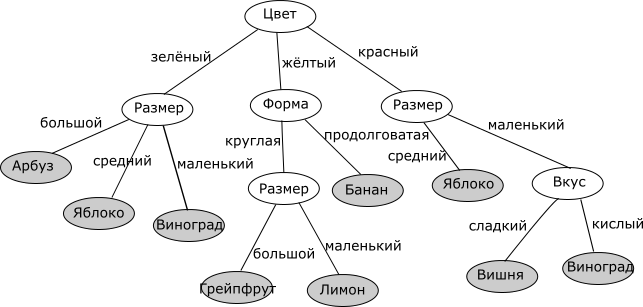
Деревья решений дают возможность извлекать правила из базы данных на естественном языке. Пример правила: Если Возраст > 35 и Доход > 200, то выдать кредит.
Деревья решений позволяют создавать классификационные модели в тех областях, где аналитику достаточно сложно формализовать знания. Алгоритм конструирования дерева решений не требует от пользователя выбора входных атрибутов (независимых переменных). На вход алгоритма можно подавать все существующие атрибуты, алгоритм сам выберет наиболее значимые среди них, и только они будут использованы для построения дерева. В сравнении, например, с нейронными сетями, это значительно облегчает пользователю работу, поскольку в нейронных сетях выбор количества входных атрибутов существенно влияет на время обучения.
Точность моделей, созданных при помощи деревьев решений, сопоставима с другими методами построения классификационных моделей (статистические методы, нейронные сети).
Разработан ряд масштабируемых алгоритмов, которые могут быть использованы для построения деревьев решения на сверхбольших базах данных; масштабируемость здесь означает, что с ростом числа примеров или записей базы данных время, затрачиваемое на обучение, т.е. построение деревьев решений, растет линейно. Примеры таких алгоритмов: SLIQ, SPRINT.
Быстрый процесс обучения. На построение классификационных моделей при помощи алгоритмов конструирования деревьев решений требуется значительно меньше времени, чем, например, на обучение нейронных сетей.
Большинство алгоритмов конструирования деревьев решений имеют возможность специальной обработки пропущенных значений.
Многие классические статистические методы, при помощи которых решаются задачи классификации, могут работать только с числовыми данными, в то время как деревья решений работают и с числовыми, и с категориальными типами данных.
Многие статистические методы являются параметрическими, и пользователь должен заранее владеть определенной информацией, например, знать вид модели, иметь гипотезу о виде зависимости между переменными, предполагать, какой вид распределения имеют данные. Деревья решений, в отличие от таких методов, строят непараметрические модели. Таким образом, деревья решений способны решать такие задачи Data Mining, в которых отсутствует априорная информация о виде зависимости между исследуемыми данными.
9.3. Процесс конструирования дерева решений
Напомним, что рассматриваемая нами задача классификации относится к стратегии обучения с учителем, иногда называемого индуктивным обучением. В этих случаях все объекты тренировочного набора данных заранее отнесены к одному из предопределенных классов.
Алгоритмы конструирования деревьев решений состоят из этапов «построение» или «создание» дерева (tree building) и «сокращение» дерева (tree pruning). В ходе создания дерева решаются вопросы выбора критерия расщепления и остановки обучения (если это предусмотрено алгоритмом). В ходе этапа сокращения дерева решается вопрос отсечения некоторых его ветвей.
Рассмотрим эти вопросы подробней.
Источник
Использование деревьев решений в задачах прогнозной аналитики
В последние десятилетия одними из самых популярных методов решения задач прогнозной аналитики являются методы построения деревьев решений. Эти методы универсальны, используют эффективную процедуру вычислений, позволяют найти достаточно качественное решение задачи. Именно об этих методах я расскажу в данной статье.
Дерево решений
Дерево решений – структура данных, в процессе обхода которой в каждом узле в зависимости от проверяемого условия принимается определенное решение – перемещение по той или иной ветке дерева от корня к «листьевым» (конечным) вершинам. В «листьевой» вершине дерева содержится искомое значение интересующего атрибута. Деревья решений могут оценивать значения категориальных атрибутов (конечное число дискретных значений), а также количественных. В первом случае говорят о задаче классификации – отнесении объекта к одному из «классов», определяемых атрибутом (например, Да/Нет, Хорошо/Удовлетворительно/Плохо и т.д.). Во втором случае говорят о задаче регрессии, то есть об оценке количественной величины.
Мы рассмотрим алгоритм, позволяющий построить такое дерево решений для оценивания и предсказания значений интересующего нас категориального атрибута анализируемого набора данных на основе значений других атрибутов (задача классификации).
Вообще способов построить дерево может быть бесконечно много – атрибуты можно рассматривать в разном порядке, проверять в узлах дерева различные условия, останавливать процесс, используя разные критерии. Но нас интересуют только деревья, которые наиболее точно оценивают значение атрибута, с минимальной ошибкой, а также позволяют выявлять зависимость между атрибутами и успешно выполнять прогнозирование значений атрибутов на новых данных. К сожалению, не существует хороших алгоритмов, позволяющих гарантированно найти такое «оптимальное» дерево (за приемлемое время). Однако существуют достаточно хорошие алгоритмы, которые пытаются построить «почти оптимальное» дерево, выполняя на каждой итерации определенный «локальный» критерий оптимальности в надежде, что получившееся дерево тоже в целом будет «оптимальным». Такие алгоритмы называются «жадными». Именно такой алгоритм мы и рассмотрим.
Алгоритм построения дерева решений
Принцип построения дерева следующий. Дерево строится «сверху вниз» от корня. Начинается процесс с определения, какой атрибут следует выбрать для проверки в корне дерева. Для этого каждый атрибут исследуется на предмет, как хорошо он в одиночку классифицирует набор данных (разделяет на классы по целевому атрибуту). Когда атрибут выбран, для каждого его значения создается ветка дерева, набор данных разделяется в соответствии со значением к каждой ветке, процесс повторяется рекурсивно для каждой ветки. Также следует проверять критерий остановки.
Главный вопрос – как выбирать атрибуты. В соответствии с идеей подхода, когда в концевых узлах дерева (листьях) будет искомый нами класс целевого атрибута, необходимо, чтобы при разбиении набора данных в каждом узле получавшиеся наборы данных были все более однородны в плане значений классов (например, большинство объектов в наборе принадлежало бы к классу Арбуз). И необходимо определить количественный критерий, чтобы оценить однородность разбиения.
Энтропия
Рассмотрим набор вероятностей pi, описывающий вероятность соответствия строки данных в нашем наборе (обозначим его X) классу i. Вычислим следующую величину:
Данная функция представляет собой так называемую энтропию. Энтропия возникла в теории информации и описывает количество информации (в битах), которое необходимо, чтобы закодировать сообщение о принадлежности случайно выбранного объекта (строки) из нашего набора X к одному из классов и передать его получателю. Если класс только один, получателю ничего не нужно передавать, энтропия равна 0 (принимается, что 0log20 = 0). Если все классы равновероятны, то потребуется log2c бит (c – общее количество классов) – максимум функции энтропии.
Далее, для выбора атрибута, для каждого атрибута A вычисляется так называемый прирост информации:
Где values(A) – все принимаемые значения атрибута A, Xa – подмножество набора данных, где A = a, |X| – количество элементов во множестве. Данная величина описывает ожидаемое уменьшение энтропии после разбиения набора данных по выбранному атрибуту. Второе слагаемое – это сумма энтропий для каждого подмножества, взятая со своим весом. Общая разница описывает, как уменьшится энтропия, сколько мы сэкономим бит для кодирования класса случайного объекта из набора X, если мы знаем значения атрибута A и разобьем набор данных на подмножества по данному атрибуту.
Алгоритм выбирает атрибут, соответствующий максимальному значению прироста информации.
Когда атрибут выбран, исходный набор разбивается на подмножества в соответствии с его значениями, исходный атрибут исключается из анализа, процесс повторяется рекурсивно.
Процесс останавливается, когда созданные подмножества стали достаточно однородны (преобладает один класс), а именно когда max(Gain(X,A)) становится меньше некоторого заданного параметра Θ (величина, близкая к 0). Как альтернативный вариант, можно контролировать само множество X, и когда оно стало достаточно мало или стало полностью однородным (только один класс), останавливать процесс.
Жадный алгоритм построения дерева решений
Более структурно алгоритм можно представить следующим образом:
1. Если max(Gain(X,A))
Источник