Простые задачи Контрольный пример
Предположим, что решения принимаются с позиции объективиста. Руководство некоторой компании решает, какую новую продукцию им производить: декоративную косметику, лечебную косметику, бытовую химию. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка:
Выигрыш, при состоянии экономической среды, руб.
Декоративная косметика (а1)
Вероятность благоприятного и неблагоприятного состояний экономической среды равна 0,5.
а основе табл. 3.1 выигрышей (потерь) можно построить дерево решений (рис. 3.1, 3.2). Обозначения — решение (решение принимает игрок); — случай (решение «принимает» случай); // — отвергнутое решение.
Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ОДО.
Рис. 3.1. Дерево решений без дополнительного обследования рынка
Рис. 3.2. Итоговое дерево решений
Определим средний ожидаемый выигрыш:
для вершины 1 ОДО1 = 0,5 * 300 000 + 0,5 * (-150 000) = 75 000 руб.;
для вершины 2 ОДО2 = 0,5 * 250 000 + 0,5 * (-70 000) = 90 000 руб.;
для вершины 3 ОДО3 = 0,5 * 100 000 + 0,5 * (-10 000) = 45 000 руб.;
Вывод. Наиболее целесообразно выбрать стратегию а2, т.е. выпускать лечебную косметику, а ветви (стратегии) а1 и а3 дерева решений можно отбросить. ОДО наилучшего решения равна 90 000 руб.
Индивидуальное задание
Решите задачу, согласно вашему варианту, используя метод дерева решений.
Вариант1
Молодой российский бизнесмен предполагает построить ночную дискотеку неподалеку от университета. По одному из допустимых проектов предприниматель может в дневное время открыть в здании дискотеки столовую для студентов. Другой вариант не связан с дневным обслуживанием клиентов. Представленные бизнес-планы показывают, что план, связанный со столовой, может принести доход в 250 тыс. рублей. Без открытия столовой бизнесмен может заработать 175 тыс. рублей Потери в случае открытия дискотеки со столовой составят 55 тыс. рублей, а без столовой — 20 тыс. рублей Определите наиболее эффективную альтернативу на основе средней стоимостной ценности в качестве критерия. Вероятность наступления благоприятного состояния равен 0,5; неблагоприятного – 0,5.
Вариант 2
Директор лицея, обучение в котором осуществляется на платной основе, решает, следует ли расширять здание лицея на 250 мест, на 50 мест или не проводить строительных работ вообще. Если население небольшого города, в котором организован платный лицей, будет расти, то большая реконструкция могла бы принести прибыль 250 тыс. рублей в год, незначительное расширение учебных помещений могло бы приносить 90 тыс. рублей прибыли. Если население города увеличиваться не будет, то крупное расширение обойдется лицею в 120 тыс. рублей убытка, а малое — 45 тыс. рублей. Однако информация о том, как будет изменяться население города, отсутствует. Постройте дерево решений и определите лучшую альтернативу.
Источник
Дерево решений
Пример №1 . Требуется принять решение о замене старого оборудования на новое того же вида или его ремонте. Отремонтированное оборудование впоследствии можно частично заменить на новое, более современное, или отремонтировать его заново.
Решение определяется будущим спросом на продукцию, которую производят на этом оборудовании.
Полная замена оборудования экономически оправдана при высоком уровне спроса. С другой стороны, можно отремонтировать старое оборудование и через один год, например, заменить его на новое, более совершенное, или заново его отремонтировать.
В данной задаче процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о замене или ремонте оборудования и решение, принимаемое через один год, относительно частичной его замены и ремонта.
Предполагается, что спрос может оказаться высоким, средним и низким.
Дерево решений имеет два типа вершин: «решающие» и «случайные» (рис.).
Рис. Дерево решений
Начиная с «решающей» вершины 1, необходимо принять решение о полной замене оборудования или его ремонте.
Вершины 2 и 3 являются «случайными». Фирма будет рассматривать возможность установления более совершенного оборудования или повторного ремонта старого в том случае, если спрос по истечении одного года установится на высоком уровне. Поэтому в вершине 4 принимается решение о частичной замене старого оборудования более совершенным или ремонте старого. Вершины 5 и 6 «случайные».
Допускается, что фирма рассматривает эту задачу на пятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого, среднего и низкого уровней спроса составляют соответственно 0,6, 0,3 и 0,1. Замена новым оборудованием того же вида, что и старое, обойдется в 2,5 млн р., а ремонт старого – в 0,8 млн р.
Затраты на частичную замену оборудования более совершенным оцениваются в 1,5 млн р., а повторный ремонт старого – в 0,8 млн р.
Ежегодные доходы для каждой стратегии фирмы следующие.
1. Замена старого оборудования на новое того же вида при высоком, среднем и низком уровнях спроса даёт соответственно 0,95, 0,7 и 0,45 млн р.
2. Ремонт старого оборудования при высоком, среднем и низком уровнях спроса оценивается соответственно в 0,3, 0,15 и 0,1 млн р.
3. Частичная замена оборудования на более совершенное при высоком, среднем и низком уровнях спроса составит соответственно 0,9, 0,6 и 0,4 млн р.
4. Повторный ремонт старого оборудования при высоком, среднем и низком уровнях спроса предполагает 0,3, 0,2 и 0,1 млн р. соответственно.
Определим оптимальную стратегию фирмы в замене оборудования.
Решение.
Оценим результаты каждой стратегии и определим, какие решения следует принимать в «решающих» вершинах 1 и 4.
Вычисления начнем с этапа 2. Для последних 4 лет альтернативы, относящиеся к вершине 4, оцениваются так:
ДЧЗ = (0,9 × 0,6 + 0,6 × 0,3 + 0,4 × 0,1) × 4 – 1,5 = 1,54 млн р.,
ДДР = (0,3 × 0,6 + 0,2 × 0,3 + 0,1 × 0,1) × 4 – 0,8 = 0,2 млн р.,
где ДЧЗ – доход от частичной замены оборудования на более совершенное; ДДР – доход от замены оборудования, прошедшего дважды ремонт.
Так как ДЧЗ > ДДР , то в вершине 4 выгоднее частично заменить оборудование на более совершенное, при этом доход составит 1,54 млн р.
Для дальнейших расчетов в вершине 4 можно оставить одну ветвь, которой соответствует доход в 1,54 млн р. за 4 года.
Вычислим доходы на 1-м этапе для «решающей» вершины 1:
ДЗН = (0,95 × 0,6 + 0,7 × 0,3 + 0,45 × 0,1) × 5 – 2,5 = 1,625 млн р.,
ДЗО = 0,3 × 0,6 × 1 + 0,15 × 0,3 × 5 + 0,1 × 0,1 × 5 +1,54 – 0,8 = 1,195 млн р.,
где ДЗН – доход от замены старого оборудования на новое того же вида; ДЗО— доход от отремонтированного оборудования и дальнейшей замены на более совершенное.
Так как ДЗН > ДЗО , то оптимальным решением в вершине 1 является полная замена старого оборудования на новое того же вида.
Итак, оптимальной стратегией фирмы в замене оборудования является полная замена старого оборудования на новое того же вида, при этом доход составит 1,625 млн р.
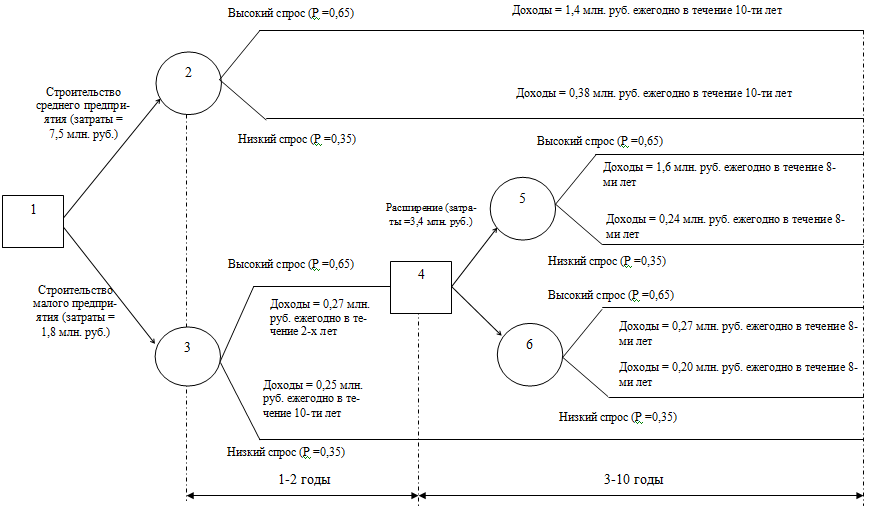
- среднее предприятие при высоком (низком) спросе – F=1,4 (K=0,38) млн. руб.;
- малое предприятие при низком спросе – L=0,25 млн. руб.;
- малое предприятие при высоком спросе – М=0,27 млн. руб.;
- расширенное предприятие при высоком (низком) спросе дает N=1,6 (P=0,24) млн. руб.;
- малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает R=0,2 млн. руб. за остальные восемь лет.
Начиная с вершины 1, являющейся «решающей», необходимо принять решение относительно размера предприятия. Вершины 2 и 3 являются «случайными». Фирма будет рассматривать возможность расширения малого предприятия только в том случае, если спрос по истечении первых двух лет установится на высоком уровне. Поэтому в вершине 4 принимается решение о расширении или не расширении предприятия. Вершины 5 и 6 будут «случайными».
Вычисления начнем со 2-го этапа. Для последних восьми лет альтернативы, относящиеся к вершине 4, оцениваются так:
— доход малого предприятия с последующим расширением:
ДР = (1,6*0,65 + 0,24*0,35)*8 – 3,4 = 5,592 млн. руб.
— доход малого предприятия без расширения
ДБР = (0,27*0,65 + 0,2*0,35)*8 = 1,964 млн. руб.
Таким образом, в вершине 4 выгоднее провести расширение, при этом доход составит 5,592 млн. руб.
Перейдем к вычислениям 1-го этапа. Для вершины 1:
— доход среднего предприятия:
ДС = (1,4*0,65 + 0,38*0,35)*10 – 7,5 = 2,93 млн. руб.
— доход малого предприятия с последующим расширением через 2 года:
ДМ = 5,592 + 0,27*0,65*2 + 0,25*0,35*10 – 1,8 = 5,018 млн. руб.
Сравнивая получаемые в вершине 1 доходы среднего и малого предприятий, видим, что более предпочтительным является вариант строительства малого предприятия с последующим расширением через 2 года.
Источник