Метод графа дерево решения

Как построить дерево решений?

Пусть нам задано некоторое обучающее множество T, содержащее объекты (примеры), каждый из которых характеризуется m атрибутами (атрибутами), причем один из них указывает на принадлежность объекта к определенному классу.

Идею построения деревьев решений из множества T, впервые высказанную Хантом, приведем по Р. Куинлену (R. Quinlan).

Пусть через 1, C₂, . C_k> обозначены классы(значения метки класса), тогда существуют 3 ситуации:

1. множество T содержит один или более примеров, относящихся к одному классу C_k. Тогда дерево решений для Т – это лист, определяющий класс C_k;
2. множество T не содержит ни одного примера, т.е. пустое множество. Тогда это снова лист, и класс, ассоциированный с листом, выбирается из другого множества отличного от T, скажем, из множества, ассоциированного с родителем;
3. множество T содержит примеры, относящиеся к разным классам. В этом случае следует разбить множество T на некоторые подмножества. Для этого выбирается один из признаков, имеющий два и более отличных друг от друга значений O₁, O₂, . O_n. T разбивается на подмножества T₁, T₂, . T_n, где каждое подмножество T_i содержит все примеры, имеющие значение O_i для выбранного признака. Это процедура будет рекурсивно продолжаться до тех пор, пока конечное множество не будет состоять из примеров, относящихся к одному и тому же классу.

Вышеописанная процедура лежит в основе многих современных алгоритмов построения деревьев решений, этот метод известен еще под названием разделения и захвата (divide and conquer). Очевидно, что при использовании данной методики, построение дерева решений будет происходит сверху вниз.

Поскольку все объекты были заранее отнесены к известным нам классам, такой процесс построения дерева решений называется обучением с учителем (supervised learning). Процесс обучения также называют индуктивным обучением или индукцией деревьев (tree induction).

На сегодняшний день существует значительное число алгоритмов, реализующих деревья решений CART, C4.5, NewId, ITrule, CHAID, CN2 и т.д. Но наибольшее распространение и популярность получили следующие два:

• CART (Classification and Regression Tree) – это алгоритм построения бинарного дерева решений – дихотомической классификационной модели. Каждый узел дерева при разбиении имеет только двух потомков. Как видно из названия алгоритма, решает задачи классификации и регрессии.
• C4.5 – алгоритм построения дерева решений, количество потомков у узла не ограничено. Не умеет работать с непрерывным целевым полем, поэтому решает только задачи классификации.

Большинство из известных алгоритмов являются «жадными алгоритмами». Если один раз был выбран атрибут, и по нему было произведено разбиение на подмножества, то алгоритм не может вернуться назад и выбрать другой атрибут, который дал бы лучшее разбиение. И поэтому на этапе построения нельзя сказать даст ли выбранный атрибут, в конечном итоге, оптимальное разбиение.

Этапы построения деревьев решений

При построении деревьев решений особое внимание уделяется следующим вопросам: выбору критерия атрибута, по которому пойдет разбиение, остановки обучения и отсечения ветвей. Рассмотрим все эти вопросы по порядку.

Источник

2.3. Задача нахождения кратчайшего пути. Дерево решений

Задача состоит в определении в транспортной сети кратчайшего пути между заданными исходным пунктом и пунктом назначения. Такая модель может быть использована для описания различных экономических ситуаций.

Введем следующие обозначения:

d_ij — расстояние на сети между смежными узлами x_i и x_j;

U_j — кратчайшее расстояние от узла x_i до узла x_j , U₁ = 0.

Алгоритм нахождения кратчайшего пути состоит в последовательном на­хождении значений U_j для каждого узла: от исходного до узла назначения. Значение U_j для каждого узла рассчитывается по формуле

где U_i — кратчайшее расстояние до предыдущего узла x_i; d_ij — расстояние между текущим узлом x_j и предыдущим узлом х_i.

Процедура заканчивается, когда получено значение U_n для узла назначения.

Кратчайший маршрут от исходного узла до узла назначения определяется начиная с узла назначения путем прохождения узлов в обратном направлении по дугам, на которых реализовались минимальные значения расстояний на каждом шаге.

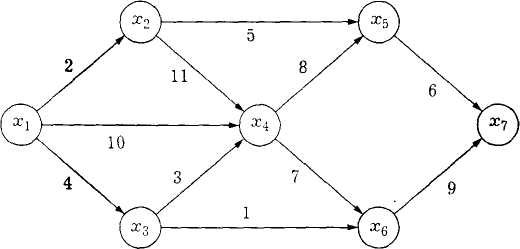
Для определения кратчайшего расстояния между узлами x₁ и x₇ получена обратная последовательность узлов и дуг:

Минимальное расстояние между узлами x₁ и x₇ равно 13, а соответствующий маршрут — 1, x₂, х₅, х₇>.

В качестве примера определения кратчайшего расстояния рассмотрим зада­чу замены автомобильного парка.

Пример 2.11. Компания по прокату автомобилей планирует замену авто­мобильного парка на очередные пять лет. Автомобиль должен проработать не менее одного года, прежде чем компания поставит вопрос о его замене. На рис. 2.33 приведен граф, который иллюстрирует стоимость замены автомобилей (в тыс. ден. ед.), зависящую от времени замены и числа лет, в течение которых автомобиль находился в эксплуатации. Определить план замены автомобилей, обеспечивающий ­ мини­мальные расходы.

Таким образом, кратчайший путь 1 — 2 — 5, стоимость — 12,1 тыс. ден. ед. Это означает, что каждый автомобиль заменяется через два года, а через пять лет списывается.

Дерево решений. На практике одно решение, как правило, приводит к необходимости принятия следующего решения и т. д. Графически подобные процессы могут быть представлены с помощью дерева решений. Дерево представляет собой связный граф без циклов, имеющий ствол и ветви, и облегчает описание многоэтапного процесса принятия управленческого решения в целом. Такое дерево дает возможность рассмотреть различные ситуации, соотнести с ними финансовые результаты, скорректировать их в соответствии с приписанной им вероятностью, а затем сравнить альтернативы и выбрать наилучший вариант действий.

Составляя дерево решений, рисуют ствол и ветви, отображающие структуру проблемы. Располагают дерево решений слева направо. Ветви обозначают альтернативные решения, которые могут быть приняты, и вероятные исходы, возникающие в результате этих решений.

Квадратные узлы на дереве решений обозначают принимаемые решения, круглые узлы — исходы. Так как влиять на исходы не представляется возмож­ным, в круглых узлах вычисляют вероятности этих исходов. Когда все решения и их исходы указаны на дереве, оценивается каждый из вариантов и проставля­ются денежные доходы. Все расходы, связанные с решениями, проставляются на соответствующих ветвях.

Рассмотрим задачу с применением дерева решений.

Пример 2.12. Компания может принять решение о строительстве среднего и малого предприятий. Малое предприятие впоследствии можно расширить. Решение определяется будущим спросом на продукцию, которую предполага­ется выпускать на сооружаемом предприятии.

Строительство среднего предприятия экономически оправдано при высоком спросе. В то же время можно построить малое предприятие и через два года его расширить. Компания рассматривает данную задачу на десятилетний период.

Анализ рыночной ситуации показывает, что вероятности высокого и низкого уровней спроса равны соответственно 0,7 и 0,3. Строительство среднего предприятия обойдется в 4 млн. руб., малого — в 1 млн руб. Затраты на расширение малого предприятия через два года оцениваются в 3,5 млн руб.

Ожидаемые ежегодные доходы для каждой из возможных альтернатив:

• среднее предприятие при высоком (низком) спросе дает 0,9 (0,2) млн руб.;
• малое предприятие при высоком (низком) спросе дает 0,2 (0,1) млн руб.;
• расширенное предприятие при высоком (низком) спросе дает 0,8 (0,1) млн руб.

Определить оптимальную стратегию компании в отношении строительства предприятий.

Решение. Данная задача является многоэтапной, так как если компания решит строить малое предприятие, то через два года она может принять решение о его расширении. В этом случае процесс принятия решения состоит из двух этапов: решения в настоящий момент о размере предприятия и решения, принимаемого через два года, о необходимости его расширения.

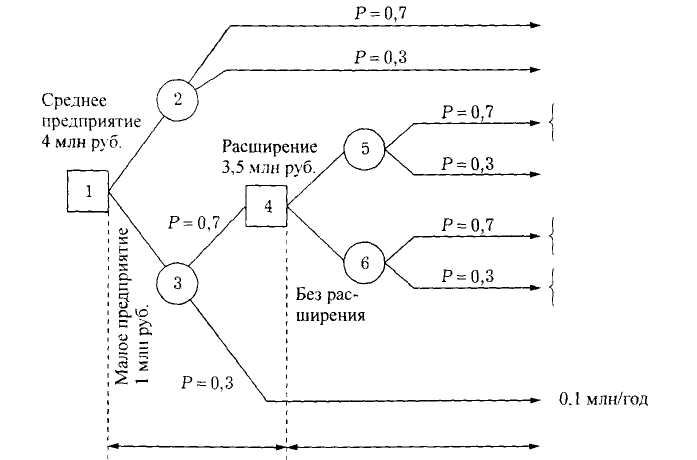
Задача представлена в виде дерева решений (рис. 2.34). Предполагается, что спрос может оказаться высоким и низким. Дерево имеет два типа вершин: «решающие» вершины обозначены квадратами, а «случайные» — кругами.

В вершине 1, являющейся «решающей», необходимо выбрать размер пред­приятия. Вершины 2 и 3 являются «случайными». Компания будет рассматривать вопрос о расширении малого предприятия только в том случае, если спрос по истечении первых двух лет установится на высоком уровне. Поэтому в вер­шине 4 принимается решение о расширении или не расширении предприятия. Вершины 5 и 6 «случайные».

Проведем расчеты для каждой из альтернатив. Вычисления начнем со 2-го этапа. Для последних восьми лет альтернативы, относящиеся к вершине 4, оцениваются:

ДР = (0,8 · 0,7 + 0,1 · 0.3) ·8-3,5 = 1,22 (млн руб.);

ДБР = (0,2 · 0,7 + 0.1 · 0,3) · 8 = 1,36 (млн руб.),

где ДР—доход в случае расширения предприятия; ДБР—доход без расширения предприятия.

Таким образом, в вершине 4 выгоднее не проводить расширение, тогда доход составит 1,36 млн руб.

Перейдем к вычислениям 1-го этапа, оставив для дальнейших расчетов одну «ветвь», выходящую из вершины 4, которой соответствует доход 1,36 млн руб. за последние восемь лет.

ДС = (0,9 · 0,7 + 0,2 · 0,3) · 10 — 4,0 = 2,9 (млн руб.);

ДМ = 1,36 + 0,2 · 0,7 · 2 + 0,1 · 0,3 · 10 — 1,0 = 0,94 (млн руб.),

где ДС — доход среднего предприятия; ДМ — доход малого предприятия.

Сравнивая полученные в вершине 1 доходы среднего и малого предприятий, видим, что предпочтительно строительство среднего предприятия.

Оценим степень риска каждого решения по величине среднеквадратического отклонения:

Рассматривая среднеквадратические отклонения, следует отметить, что строительство малого предприятия дает более гарантированный доход.

Источник