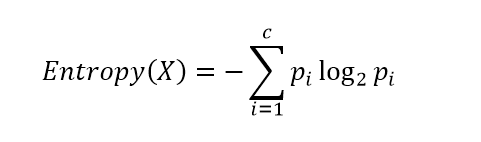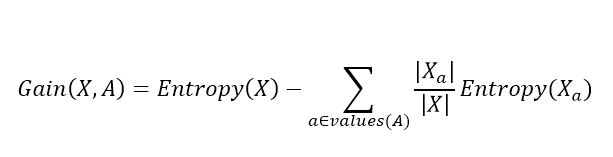Методы интеллектуального анализа деревья решений

Использование деревьев решений в задачах прогнозной аналитики

В последние десятилетия одними из самых популярных методов решения задач прогнозной аналитики являются методы построения деревьев решений. Эти методы универсальны, используют эффективную процедуру вычислений, позволяют найти достаточно качественное решение задачи. Именно об этих методах я расскажу в данной статье.

Дерево решений

Дерево решений – структура данных, в процессе обхода которой в каждом узле в зависимости от проверяемого условия принимается определенное решение – перемещение по той или иной ветке дерева от корня к «листьевым» (конечным) вершинам. В «листьевой» вершине дерева содержится искомое значение интересующего атрибута. Деревья решений могут оценивать значения категориальных атрибутов (конечное число дискретных значений), а также количественных. В первом случае говорят о задаче классификации – отнесении объекта к одному из «классов», определяемых атрибутом (например, Да/Нет, Хорошо/Удовлетворительно/Плохо и т.д.). Во втором случае говорят о задаче регрессии, то есть об оценке количественной величины.

Мы рассмотрим алгоритм, позволяющий построить такое дерево решений для оценивания и предсказания значений интересующего нас категориального атрибута анализируемого набора данных на основе значений других атрибутов (задача классификации).

Вообще способов построить дерево может быть бесконечно много – атрибуты можно рассматривать в разном порядке, проверять в узлах дерева различные условия, останавливать процесс, используя разные критерии. Но нас интересуют только деревья, которые наиболее точно оценивают значение атрибута, с минимальной ошибкой, а также позволяют выявлять зависимость между атрибутами и успешно выполнять прогнозирование значений атрибутов на новых данных. К сожалению, не существует хороших алгоритмов, позволяющих гарантированно найти такое «оптимальное» дерево (за приемлемое время). Однако существуют достаточно хорошие алгоритмы, которые пытаются построить «почти оптимальное» дерево, выполняя на каждой итерации определенный «локальный» критерий оптимальности в надежде, что получившееся дерево тоже в целом будет «оптимальным». Такие алгоритмы называются «жадными». Именно такой алгоритм мы и рассмотрим.

Алгоритм построения дерева решений

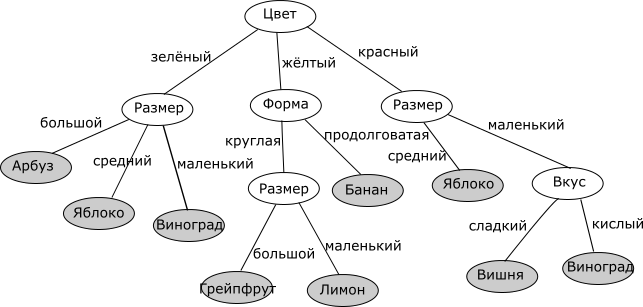
Принцип построения дерева следующий. Дерево строится «сверху вниз» от корня. Начинается процесс с определения, какой атрибут следует выбрать для проверки в корне дерева. Для этого каждый атрибут исследуется на предмет, как хорошо он в одиночку классифицирует набор данных (разделяет на классы по целевому атрибуту). Когда атрибут выбран, для каждого его значения создается ветка дерева, набор данных разделяется в соответствии со значением к каждой ветке, процесс повторяется рекурсивно для каждой ветки. Также следует проверять критерий остановки.

Главный вопрос – как выбирать атрибуты. В соответствии с идеей подхода, когда в концевых узлах дерева (листьях) будет искомый нами класс целевого атрибута, необходимо, чтобы при разбиении набора данных в каждом узле получавшиеся наборы данных были все более однородны в плане значений классов (например, большинство объектов в наборе принадлежало бы к классу Арбуз). И необходимо определить количественный критерий, чтобы оценить однородность разбиения.

Энтропия

Рассмотрим набор вероятностей pi, описывающий вероятность соответствия строки данных в нашем наборе (обозначим его X) классу i. Вычислим следующую величину:

Данная функция представляет собой так называемую энтропию. Энтропия возникла в теории информации и описывает количество информации (в битах), которое необходимо, чтобы закодировать сообщение о принадлежности случайно выбранного объекта (строки) из нашего набора X к одному из классов и передать его получателю. Если класс только один, получателю ничего не нужно передавать, энтропия равна 0 (принимается, что 0log20 = 0). Если все классы равновероятны, то потребуется log2c бит (c – общее количество классов) – максимум функции энтропии.

Далее, для выбора атрибута, для каждого атрибута A вычисляется так называемый прирост информации:

Где values(A) – все принимаемые значения атрибута A, Xa – подмножество набора данных, где A = a, |X| – количество элементов во множестве. Данная величина описывает ожидаемое уменьшение энтропии после разбиения набора данных по выбранному атрибуту. Второе слагаемое – это сумма энтропий для каждого подмножества, взятая со своим весом. Общая разница описывает, как уменьшится энтропия, сколько мы сэкономим бит для кодирования класса случайного объекта из набора X, если мы знаем значения атрибута A и разобьем набор данных на подмножества по данному атрибуту.

Алгоритм выбирает атрибут, соответствующий максимальному значению прироста информации.

Когда атрибут выбран, исходный набор разбивается на подмножества в соответствии с его значениями, исходный атрибут исключается из анализа, процесс повторяется рекурсивно.

Процесс останавливается, когда созданные подмножества стали достаточно однородны (преобладает один класс), а именно когда max(Gain(X,A)) становится меньше некоторого заданного параметра Θ (величина, близкая к 0). Как альтернативный вариант, можно контролировать само множество X, и когда оно стало достаточно мало или стало полностью однородным (только один класс), останавливать процесс.

Жадный алгоритм построения дерева решений

Более структурно алгоритм можно представить следующим образом:

1. Если max(Gain(X,A))

Источник

Деревья решений и алгоритмы их построения

Сегодня мы поговорим об одном из классических методов интеллектуального анализа данных (англ. data mining) – построении деревьев решений, расскажем о его основных принципах и подробнее остановимся на алгоритмах его реализации.

Что такое дерево принятия решений?

Согласно наиболее общему определению, дерево принятия решений – это средство поддержки принятия решений при прогнозировании, широко применяющееся в статистике и анализе данных. Нас с вами больше интересует второй вариант использования, однако прежде чем перейти к вопросам о пользе деревьев решений для мира больших данных и конкретным алгоритмам, хотелось бы упомянуть о важнейших понятиях, связанных с методом в целом.

Итак, дерево решений, подобно его «прототипу» из живой природы, состоит из «ветвей» и «листьев». Ветви (ребра графа) хранят в себе значения атрибутов, от которых зависит целевая функция; на листьях же записывается значение целевой функции. Существуют также и другие узлы – родительские и потомки – по которым происходит разветвление, и можно различить случаи.

Пример использования

Цель всего процесса построения дерева принятия решений – создать модель, по которой можно было бы классифицировать случаи и решать, какие значения может принимать целевая функция, имея на входе несколько переменных.

Как пример, представим случай, когда необходимо принять решение о выдаче кредита (целевая функция может принимать значения «да» и «нет») на основе информации о клиенте (несколько переменных: возраст, семейное положение, уровень дохода и так далее). К примеру, переменная «возраст» с атрибутом «менее 21 одного года = да» сразу приведет от корневого узла дерева к его листу, причем целевая функция «выдача кредита» примет значение «нет». Если возраст составляет более 21 года, то ветвь приведет нас к очередному узлу, который, к примеру, «спросит» нас об уровне дохода клиента. Таким образом, классификация каждого нового случая происходит при движении вниз до листа, который и укажет нам значение целевой функции в каждом конкретном случае.

Общий алгоритм построения дерева принятия решения

Предлагаем рассмотреть на нашем примере общий алгоритм построения дерева, чтобы затем перейти к его частным случаям:

• Вначале необходимо выбрать атрибут Q (в нашем случае, допустим: уровень дохода > 500$ в месяц) и поместить его в корневой узел.
• Затем, из наших тестовых примеров (или набора данных) для каждого значения атрибута i (в нашем случае их два – «да» и «нет») выбираем только те, для которых Q=i.
• Далее, рекурсивно строим дерево принятия решений.

Основная проблема, очевидно, кроется в первом шаге – на каком основании выбирается каждый следующий атрибут Q? На этот вопрос существует несколько ответов в виде частных алгоритмов принятия решений – главными из которых являются алгоритмы ID3, C4.5 и CART

Основные частные алгоритмы

1. ID3. В основе этого алгоритма лежит понятие информационной энтропии – то есть, меры неопределенности информации (обратной мере информационной полезности величины). Для того чтобы определить следующий атрибут, необходимо подсчитать энтропию всех неиспользованных признаков относительно тестовых образцов и выбрать тот, для которого энтропия минимальна. Этот атрибут и будет считаться наиболее целесообразным признаком классификации.
2. C5. Этот алгоритм – усовершенствование предыдущего метода, позволяющее, в частности, «усекать» ветви дерева, если оно слишком сильно «разрастается», а также работать не только с атрибутами-категориями, но и с числовыми. В общем-то, сам алгоритм выполняется по тому же принципу, что и его предшественник; отличие состоит в возможности разбиения области значений независимой числовой переменной на несколько интервалов, каждый из которых будет являться атрибутом. В соответствии с этим исходное множество делится на подмножества. В конечном итоге, если дерево получается слишком большим, возможна обратная группировка – нескольких узлов в один лист. При этом, поскольку перед построением дерева ошибка классификации уже учтена, она не увеличивается.
3. CART. Алгоритм разработан в целях построения так называемых бинарных деревьев решений – то есть тех деревьев, каждый узел которых при разбиении «дает» только двух потомков. Грубо говоря, алгоритм действует путем разделения на каждом шаге множества примеров ровно напополам – по одной ветви идут те примеры, в которых правило выполняется (правый потомок), по другой – те, в которых правило не выполняется (левый потомок). Таким образом, в процессе «роста» на каждом узле дерева алгоритм проводит перебор всех атрибутов, и выбирает для следующего разбиения тот, который максимизирует значение показателя, вычисляемого по математической формуле и зависящего от отношений числа примеров в правом и левом потомке к общему числу примеров.

Резюме

Деревья принятий решений – один из основных и наиболее популярных методов помощи в принятии решений. Действительно, построение деревьев решений позволяет наглядно продемонстрировать другим и разобраться самому в структуре данных, создать работающую модель классификации данных, какими бы «большими» они ни были.

Источник