Минимальное покрывающее дерево сети

остовного дерева сети

В экономических приложениях графы принято называть сетями, а их вершины — узлами. Каждому ребру (дуге) придают некоторое числовое значение, которое в зависимости от смысла задачи может обозначать расстояние, пропускную способность, время и т.д. С каждым видом сети связан определенный тип потоков (например, поток нефти в нефтепроводах, автомобильные потоки в сети городских дорог).

Определение 1. Остовным деревом сети называется дерево, содержащее все узлы сети.

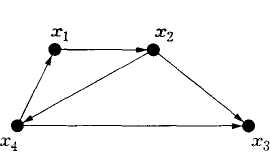
Пример 1. Рассмотрим сеть с пятью узлами:

Для данной сети можно построить следующие остовные деревья:

и т.д. Можно утверждать, что для данной сети существует множество остовных деревьев.

При изучении сетей возникает задача построения минимального остовного дерева, т.е. задача соединения всех узлов сети с помощью путей наименьшей длины. Примером такой задачи является проектирование сети дорог, соединяющих населенные пункты, где дороги, соединяющие два пункта, могут проходить через другие населенные пункты. Наиболее экономичный проект должен минимизировать общую длину дорог.

Рассмотрим процедуру построения минимального остовного дерева. Обозначим:

X = < x ₁ , x ₂ , …, x _n > — множество узлов сети;

C _k — связное множество узлов сети, соединенных алгоритмом после выполнения k -й итерации.

— множество узлов сети, не соединенных с узлами множества C _k после выполнения k -й итерации.

Алгоритм построения минимального остовного дерева сети

1. Выбрать произвольный узел сети x _i , C ₁ = < x_i >, = X \ < x_i >.

2. Выбрать из оставшихся узлов узел x _j , ближайший к множеству узлов C ₁ , C ₂ = < x_i , x _j >, = X \ < x_i , x _j >.

3. Выбрать из множества узел, ближайший к узлам множества C ₂ , включить его в множество C ₂ и исключить из множества .

За конечное число шагов будут обработаны все узлы сети и построено минимальное остовное дерево. C _n = X , = f .

Пример 2. Телевизионная компания планирует подключение к кабельной сети пяти новых районов. Структура планируемой сети и расстояния между пунктами заданы рисунком.

Источник

2.2. Ориентированные графы. Построение минимального остовного дерева сети

Понятие ориентированного графа лежит в основе решения многих прикладных задач, имеющих непосредственное отношение к задачам логистики. Одной из таких задач является построение минимального остовного дерева сети. При изучении сетей возникает названная задача, т. е. задача соединения всех узлов сети с помощью путей наименьшей длины. Примером такой задачи является проектирование сети дорог между населенными пунктами, где дороги, соединяющие два пункта, могут проходить через другие населенные пункты. Наиболее экономичный проект должен минимизировать общую длину дорог.

Ребро графа G(X, Т) называется ориентированным, или дугой, если одну вершину считают началом, а другую концом этого ребра

На рисунке дугу обозначают стрелкой. Дугу с началом в вершине x_i и концом в вершине x_j записывают (x_i, x_j).

Определение2.7. Граф, все ребра которого ориентированы, называется ориентированным графом.

Число дуг, исходящих из вершины ориентированного графа x_i, называется полустепенью исхода вершины x_i, число дуг, входящих в вершину x_i, − полустепенью захода вершины x_i.

Вершина x_i называется источником, если ее полустепень захода равна нулю, и стоком, если ее полустепень исхода равна нулю.

Рассмотрим ориентированный граф на рисунке 2.25. Полустепень исхода вершины х₁ равна 1, полустепень захода этой вершины – 2, степень вершины х₁ равна 3. Вершина х₃ является источником, вершина х₂ – стоком.

Определение 2.8. Последовательность дуг (x₁, x₂), (x₂, x₃), …, (x_k-1, x_k), в которой конец предыдущей дуги совпадает с началом следующей, называется маршрутом от x₁ до x_k .

Маршрут, в котором первая и последняя вершины совпадают, называется замкнутым.

Маршрут, в котором все вершины различны, называется путем от x₁ до x_k.

Если существует путь из вершины x_i в вершину x_j, то говорят, что x_j достижима из x_i.

Замкнутый путь называется контуром.

Полным ориентированным графом называется граф G(X, Т), в котором каждая пара вершин соединена в точности одной дугой.

Ориентированный граф, изображенный на рис.2.28, является полным.

Ориентированный граф G(X.T) можно задать с помощью матрицы инци­дентности. Пусть x₁, x₂, . х_n — вершины графа, 1₁, 1₂, …, l_m — дуги графа.

Определение 2.9. Матрицей инцидентности ориентированного графа G(X, T) называется матрица В_{n х m}, у которой элемент b_ij равен 1, если дуга l_j исходит из вершины x_i, равен (−1), если дуга l_j входит в вершину x_i; равен 0, если дуга l_j и вершина x_i не инцидентны.

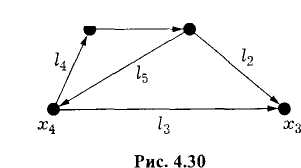
Пример 2.7. Для ориентированного графа, изображенного на рис. 2.29, матрица инцидентности имеет следующий вид:

Построение минимального остовного дерева сети. В экономических приложениях графы принято называть сетями, а их верши­ны — узлами. Каждому ребру (дуге) придают некоторое числовое значение, которое в зависимости от смысла задачи может обозначать расстояние, про­пускную способность, время и т. д. С каждым видом сети связан определенный тип потоков например, поток нефти в нефтепроводах, автомобильные потоки в сети городских дорог).

Определение 2.10. Остовным деревом сети называется дерево, содержа­щее все узлы сети.

Пример 2.8. Рассмотрим сеть с пятью узлами (рис. 2.30, а). Для этой сети можно построить множество остовных деревьев. Некоторые примеры таких остовных деревьев изображены на рис. 2.30, б-е.

Источник

Алгоритм Краскала, Прима для нахождения минимального остовного дерева

Алгоритмы нахождения MST применимы в различных областях, начиная от кластеризации данных до построения компьютерных, транспортных сетей.
Я надеюсь, что вы после прочтения данной статьи, примерно понимали, как работают жадные алгоритмы нахождения MST.

Формальная постановка задачи

Имеется следующий неориентированный взвешенный граф. Назовем остовным деревом подграф, содержащий все вершины исходного графа, который является деревом. И задача состоит в том, чтобы найти такое остовное дерево, сумма рёбер которого минимальна.

Неформальная постановка задачи

Представьте исходный граф без рёбер, теперь вам нужно как-то соединить все вершины между собой, чтобы можно было бы попасть из любой вершины в другую, не имея при этом циклов в получившемся графе с минимально возможной суммой весов включенных рёбер.

Алгоритм Краскала

Механизм, по которому работает данный алгоритм, очень прост. На входе имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева. Будем рассматривать только связные графы, в другом случае при применении алгоритма Краскала мы будем получать не минимальное остовное дерево, а просто остовной лес.

• Вначале мы производим сортировку рёбер по неубыванию по их весам.
• Добавляем i-ое ребро в наш подграф только в том случае, если данное ребро соединяет две разные компоненты связности, одним из которых является наш подграф. То есть, на каждом шаге добавляется минимальное по весу ребро, один конец которого содержится в нашем подграфе, а другой — еще нет.
• Алгоритм завершит свою работу после того, как множество вершин нашего подграфа совпадет с множеством вершин исходного графа.

Данный алгоритм называется жадным из-за того, что мы на каждом шаге пытаемся найти оптимальный вариант, который приведет к оптимальному решению в целом.

Разбор конкретного примера по шагам

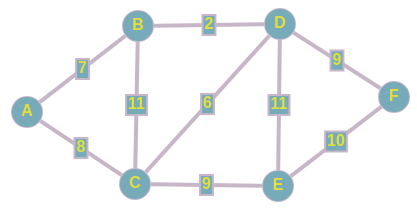
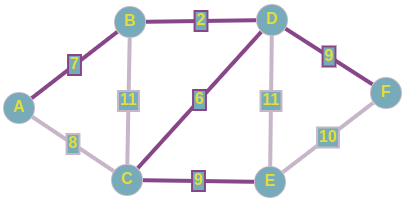
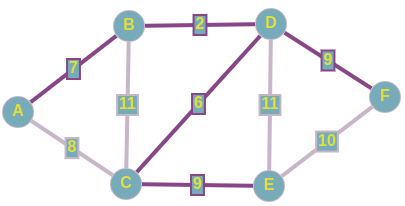
Из представленного сверху графа, выпишем все его ребра в отсортированном порядке:

1) D B; w = 2
2) D C; w = 6
3) A B; w = 7
4) A C; w = 8
5) C E; w = 9
6) D F; w = 9
7) F E; w = 10
8) B C; w = 11
9) D E; w = 11

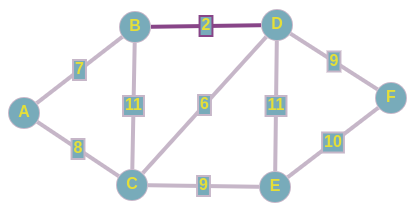
И начнем по списку добавлять эти ребра в наш остов:

При добавлении в наше остовное дерево ребра A C, как вы можете заметить, образовывается цикл, поэтому мы просто пропускаем данное ребро.

По итогу у нас образовывается следующий подграф, и как вы заметили, мы соединили все вершины ребрами с минимально-возможными весами, а значит, нашли минимальное остовное дерево для нашего исходного графа.

Проводим проверку с помощью встроенного алгоритма для нахождения MST на graphonline, и видим, что подграфы идентичны.
И да, из-за того, что при равенстве весов рёбер мы можем выбрать любое из них, конечные подграфы, являющиеся минимальными остовными деревьями, могут различаться с точностью до некоторых рёбер.

Суммарный вес искомого MST равен 33.

Реализация

Реализовать представленный алгоритм проще всего с помощью СНМ(система непересекающихся отрезков).

Вначале, как мы уже раннее говорили, необходимо отсортировать ребра по неубыванию по их весам. Далее с помощью вызовов функции make_set() мы каждую вершину можем поместить в свое собственное дерево, то есть, создаем некоторое множество подграфов. Дальше итерируемся по всем ребрам в отсортированном порядке и смотрим, принадлежат ли инцидентные вершины текущего ребра разным подграфам с помощью функции find_set() или нет, если оба конца лежат в разных компонентах, то объединяем два разных подграфа в один с помощью функции union_sets().

В итоге асимптотическая сложность данного алгоритма сводится к:

, где:
sort() —
make_set()-
find_set —
union_sets —

vector parent, rank; void make_set(int v) < parent[v] = v; rank[v] = 0; >int find_set(int v) < if (v == parent[v]) return v; return parent[v] = find_set(parent[v]); >void union_sets(int a, int b) < a = find_set(a); b = find_set(b); if (a != b) < if (rank[a] < rank[b]) swap(a, b); parent[b] = a; if (rank[a] == rank[b]) rank[a]++; >> struct Edge < int u, v, weight; bool operator<(Edge const& other) < return weight < other.weight; >>; int n; vector edges; int cost = 0; vector result; parent.resize(n); rank.resize(n); for (int i = 0; i < n; i++) make_set(i); sort(edges.begin(), edges.end()); for (Edge e : edges) < if (find_set(e.u) != find_set(e.v)) < cost += e.weight; result.push_back(e); union_sets(e.u, e.v); >>

Алгоритм Прима

Суть самого алгоритма Прима тоже сводится к жадному перебору рёбер, но уже из определенного множества. На входе так же имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева.

• Изначально наш подграф состоит из одной любой вершины исходного графа.
• Затем из рёбер инцидентных этой вершине, выбирается такое минимальное ребро, которое связала бы две абсолютно разные компоненты связности, одной из которых и является наш подграф. То есть, как только у нас появляется возможность добавить новую вершину в наш подграф, мы тут же включаем ее по минимальмально возможному весу.
• Продолжаем выполнять предыдущий шаг до тех пор, пока не найдем искомое MST.

Разбор конкретного примера

Выбираем чисто случайно вершину E, далее рассмотрим все ребра исходящие из нее, включаем в наше остовное дерево ребро C E; w = 9, так как данное ребро имеет минимальный вес из всех рёбер инцидентных множеству вершин нашего подграфа. Имеем следующее:

Теперь выборка производится из рёбер:
D C; w = 6
A C; w = 8
F E; w = 10
B C; w = 11
D E; w = 11

То есть, в данный момент, мы знаем только о двух вершинах, соответственно, знаем о всех ребрах, исходящих из них. Про связи между другими вершинами, которые не включены в наш подграф, мы ничего не знаем, поэтому они на этом шаге не рассматриваются.

Добавляем в наш подграф ребро D C и по аналогии добаляем ребро D B . Получаем следующее:

Давайте добьем наш подграф до минимального остовного дерева. Вы, наверное, уже догадались о том, по каким ребрам мы будем связывать наши оставшиеся вершины:
A и F.

Проводим последние штрихи и получили тот же самый подграф в качестве минимального остовного дерева. Но как мы раннее говорили, сам подграф ничего не решает, главное тут — множество рёбер, которые включены в наше остовное дерево.

Суммарный вес искомого MST равен 33.

Источник