Модель разрешающих деревьев это

математическая-логика — Сложность вычисления дизъюнкции

Какова сложность вычисления дизъюнкции $$\bigvee_ x_$$ в модели разрешающих деревьев?

задан 6 Фев ’18 21:21

@Oldfield: а какова циркумполярная элоквенция бозона Хиггса в переменном магнитном поле эквипотенциального соленоида для уравнения Кадомцева — Петвиашвили второго рода? 🙂

Это я к той простой мысли, что любые понятия, не относящиеся к обязательной части математических курсов, следует сопровождать пояснениями или ссылками. Иными словами, понятие дизъюнкции знают все, а вот про «модель разрешающих деревьев» слышали только «избранные» 🙂

@falcao Разрешающие деревья для булевых функций. В этой модели требуется вычислить булеву функцию f : ^n → , то есть на вход подается ~x = (x1, . . . , xn) ∈ ^n и при этом за один ход разрешается спрашивать значение одной переменной из x1, . . . , xn. Формально в рамках нашей общей модели это означает, что в промежуточных вершинах разрешающего дерева могут быть написаны только подмножества множества ^n, состоящие из всех векторов, в которых одна фиксированная координата одинакова.

Но на самом деле удобно в случае булевых функцию в промежуточных вершинах дерева просто писать переменную, которую мы спрашиваем, и в пути, соответствующему вычислению, переходить по ребру помеченному нулем, если эта переменная равна нулю, и по ребру помеченному единицей, если переменная равна единице

@Oldfield: если подходить без лишних формальностей, то не будет ли тогда ответом число n? Ясно, что n вопросов заведомо хватает, а меньшего числа уже нет, так как если мы не все переменные знаем, и там везде 0, то значение дизъюнкции нам не известно. Это всё слишком просто выглядит; может ли такое упражнение быть предложено?

@falcao Да, слишком просто, что и вызывает сомнения, но меньше n точно нельзя, а больше смысла нет

@Oldfield: у меня сейчас практически не осталось сомнений в том, что здесь имелось в виду именно это простое решение. Я смотрел в Сети ту лекцию, в которой встречался термин «модель разрешающих деревьев» — там рассматривались именно такие простенькие примеры, когда шёл разговор о функциях и сложности их вычисления.

Источник

ТМВ-2020-Лекция-04.02.2020

Разрешающее дерево — бинарное дерево, в котором каждая вершина содержит некоторое действие, в случае сортировки — сравнение. Из каждой вершины выходит два ребра, одно из них достигается, если i-й элемент больше j-го; другое — если i-й элемент меньше j-го. Вычисление на конечном наборе входных значений (массив чисел) происходит следующем образом: в начале вычисления мы находимся в корне дерева. Находясь в какой-либо вершине, мы смотрим на значения i-го и j-го элементов. Если i-й элемент больше j-го, то переходим в следующую вершину по 1-му ребру(левому), если i-й элемент меньше j-го, то переходим в следующую вершину по 2-му ребру(правому). На листьях(выходе) мы получаем итоговую перестановку \(\pi\).

Вычислительная сложность алгоритма сортировки

Минимальное количество сравнений — длина пути из корня в лист. В массиве всего n элементов, соответственно листьев будет: $$m \geq \log_2 m \geq \log_2 n! \approx /$$по Формуле Стирлинга $$n! \sim \sqrt<2\pi n>(\frac)^n/ \approx \log_2<\sqrt<2\pi n>(\frac)^n> = const + n\log_2 n \approx n\log_2 n$$

Бинарный счётчик

Бинарный счётчик

Бинарный счетчик – массив, состоящий из \(n\) бит, в котором записано двоичное число, и определена одна операция — инкремент: \(Inc()\) (сложность операции \(O(n)\)).

Пример счётчика:

1	0	1	.	1	0	0
1	2	3	.	n-2	n-1	n

Пример операции

Исходный массив
0	1	1	1	1	1
Результирующий массив(применение Inc())
1	0	0	0	0	0

Если цепь из \(m\) инкрементов: сложность \(O(m*n)\), в хорошем случае \(O(m)\).

Посмотрим на изменения ячеек при проведении операции \(Inc()\) \(m\) раз.

Оценка сложности

Оценка сложности:$$m + \frac + \frac + \frac + \ldots \le \sum_^\infty \frac = m\sum_^\infty \frac = 2m$$
Пояснение:

$$q(1 + q + \ldots + q^ + q^n — q^n) = q(1 + Q_n — q^n) = Q_n$$

Амортизационный анализ

Наряду с получением верхних и нижних оценок и оценок в среднем, часто используются так называемые амортизационные оценки. Амортизационный анализ — подход к оценке вычислительной сложности алгоритма. Амортизационный анализ применяется при оценке времени выполнения корректной последовательности, состоящей из однотипных или разнотипных операций с некоторой структурой данных. Учетная сложность — сложность в среднем на длительной цепочке операций.

Метод потенциалов

\(t_i\) — время выполнения операции(истинная стоимость операции)

\(c_\) — учётная(приведённая) стоимость операции

\(\Phi_\) — потенциал (функция состояния, принимает на вход текущее состояние структуры данных и возвращает некоторое неотрицательное число)

$$\sum_^mt_i = \sum_^m(c_i + \Phi_i — \Phi_) = \sum_^mc_i + \Phi_1 — \Phi_m$$ (если правая часть данного выражения является ограниченной, то алгоритм является линейным)

Если \(c_i = const\), то \(\sum_^mt_i = mc + \Phi_i — \Phi_m = O(mc + \Phi_i — \Phi_m ) \)

Пример: задача про бинарный счётчик

Как нужно выбрать функцию потенциала с тем, чтобы скорректированная с помощью этой функции потенциала стоимость оказалась равномерно ограничена по всем операциям?

Потенциалом состояния назовем число единиц в этом состоянии \( \Phi\) — количество единиц

Разность потенциалов – количество ячеек, в которые вносим изменения.

\(t_ = k+1 = c_ + \Phi_i — \Phi_ = t_ + k — 1 \Rightarrow c_i = 2\)

\(O(mc + \Phi_1 — \Phi_m) = O(2m + 0 — 0\) (пояснение: минимальная оценка)\() = O(m)\)

Динамический массив

Пусть динамический массив строится так:

2) Элементы добавляются в него по одному. При исчерпании места в массиве выделяется новый участок памяти, в котором зарезервировано дополнительно \(l\) элементов

3) Все уже присутствовавшие в массиве элементы копируются в новый участок памяти

4) Добавляется очередной элемент.

Сколько суммарно копирований элементов необходимо осуществить, если всего добавляется \(n=kl\) элементов?

На первом шаге мы копируем \(l\) элементов, затем \(2l\), затем \(3l\), и так далее, вплоть до \(n-l\) элементов. Сумма этих количеств:

\(t_ = c_ — n_i + s_i + n_ = c_ — 1 = 1 \Rightarrow c_ = 2\)

\(t_ = s_i + 1 = c_ — n_i + s_i + n_ — s_ = c_ + 2s_i -s_i — 1 = c_ + s_i — 1 = s_i + 1\)

\(n + \frac + \frac + \cdots + \frac \le 2n\)

Источник

математическая-логика — Сложность вычисления дизъюнкции

Какова сложность вычисления дизъюнкции $$\bigvee_ x_$$ в модели разрешающих деревьев?

задан 6 Фев ’18 21:21

@Oldfield: а какова циркумполярная элоквенция бозона Хиггса в переменном магнитном поле эквипотенциального соленоида для уравнения Кадомцева — Петвиашвили второго рода? 🙂

Это я к той простой мысли, что любые понятия, не относящиеся к обязательной части математических курсов, следует сопровождать пояснениями или ссылками. Иными словами, понятие дизъюнкции знают все, а вот про «модель разрешающих деревьев» слышали только «избранные» 🙂

@falcao Разрешающие деревья для булевых функций. В этой модели требуется вычислить булеву функцию f : ^n → , то есть на вход подается ~x = (x1, . . . , xn) ∈ ^n и при этом за один ход разрешается спрашивать значение одной переменной из x1, . . . , xn. Формально в рамках нашей общей модели это означает, что в промежуточных вершинах разрешающего дерева могут быть написаны только подмножества множества ^n, состоящие из всех векторов, в которых одна фиксированная координата одинакова.

Но на самом деле удобно в случае булевых функцию в промежуточных вершинах дерева просто писать переменную, которую мы спрашиваем, и в пути, соответствующему вычислению, переходить по ребру помеченному нулем, если эта переменная равна нулю, и по ребру помеченному единицей, если переменная равна единице

@Oldfield: если подходить без лишних формальностей, то не будет ли тогда ответом число n? Ясно, что n вопросов заведомо хватает, а меньшего числа уже нет, так как если мы не все переменные знаем, и там везде 0, то значение дизъюнкции нам не известно. Это всё слишком просто выглядит; может ли такое упражнение быть предложено?

@falcao Да, слишком просто, что и вызывает сомнения, но меньше n точно нельзя, а больше смысла нет

@Oldfield: у меня сейчас практически не осталось сомнений в том, что здесь имелось в виду именно это простое решение. Я смотрел в Сети ту лекцию, в которой встречался термин «модель разрешающих деревьев» — там рассматривались именно такие простенькие примеры, когда шёл разговор о функциях и сложности их вычисления.

Источник

Разрешающее дерево сортировки сравнениями

В предыдущих разделах были рассмотрены различные алгоритмы, которые могут отсортировать п чисел за время О (п ×log n). Алгоритмы сортировки слиянием (merge sort) и сортировки с помощью кучи (heap sort) работают за такое время в худшем случае, а у алгоритма быстрой сортировки таковым является среднее время работы. Оценка O (n ×log n) точна: для каждого из этих алгоритмов можно предъявить последовательность из п чисел, время обработки которой будет W(n ×log n).

Все упомянутые алгоритмы проводят сортировку, основываясь исключительно на попарных сравнениях элементов, поэтому их иногда называют сорти­ровками сравнением (comparison sort). В дальнейшем будет доказано, что алгоритм такого типа сортирует п элементов за время не меньше W(n ×log n) в худшем случае. Тем самым алгоритмы сортировки слиянием и с помощью кучи асимптотически оптимальны: не существует алгоритма сортировки сравнением, который превосходил бы указанные алгоритмы более чем в конечное число раз.

Три алгоритма сортировки – сортировка подсчётом, цифровая сортировка и сортировка вычерпыванием могут работать за линейное время. Разумеется, они улучшают оценку W(n ×log n) за счёт того, что используют не только попарные сравнения, но и внутреннюю структуру сортируемых объектов, т.е. дополнительную априорную информацию. Без использования дополнительной информации сортировка за линейное время невозможна.

Говорят, что алгоритм сортировки основан на сравнениях, если он никак не использует внутреннюю структуру сортируемых элементов, а лишь сравнивает их и после некоторого числа сравнений выдаёт ответ (указывающий истин­ный порядок элементов).

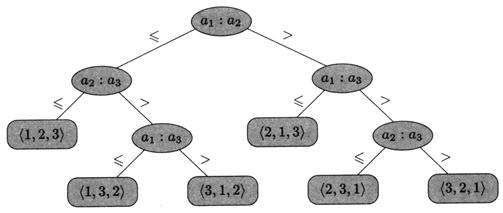
На рис. 2.8 изображено разрешающее дерево (decision tree), соответствующее сортировке последовательности из трёх элементов с по­мощью алгоритма сортировки вставками.

Рисунок 2.8 – Разрешающее дерево сортировки вставками

Поскольку число перестановок из трёх элементов равно 3! = 6, у дерева должно быть не менее 6 листьев. Поскольку двоичное дерево высоты h имеет не более 2 h листьев, имеем n! ≤ 2 h . Логарифмируя это неравенство по основанию 2 и пользуясь неравенством п! > (п / е) п , вытекающим из формулы Стирлинга , получаем, что

что и утверждалось. Наилучшее время работы алгоритма сортировки сравнениями есть O (n ×log n), причем эта оценка не может быть асимптотически улучшена (т.к. доказано, что нижний предел для любой сортировки сравнениями, не использующей дополнительной информации есть W(n ×log n)).

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник