Найти код дерева методом прюфера

Создание графа

С помощью данной программы можно онлайн нарисовать любой граф (ориентированный, неориентированный, с петлями), сетевой график, дерево, граф состояний или блок-схему. Во вкладке Примеры графов можно ознакомиться с возможностями онлайн сервиса.
Граф можно нарисовать или задать в виде матрицы или схемы (меню Действия ).

• Поиск кратчайшего пути с помощью алгоритма Дейкстры, задача о кратчайшем пути (см. вкладку Параметры графа ).
• Построить дерево.
• Построить дерево по коду Прюфера (затем можно будет найти его инверсию).

• Редактор графа
• Параметры графа
• Решение
• Примеры реализаций
• Оформление Word

Размеры графического полотна

Созданный граф можно сохранить в форматах docx и png (меню Действия ). Далее можно найти характеристики графа (матрица смежности, матрица инциденций, матрица расстояний).

Граф состояний кредитной карты

Здесь объектом анализа выступает такой банковский продукт как кредитная карта K . На графе состояний операций по кредитной карте отмечены следующие события: начисления процентов на остаток счета ( P — петля), покупка П на сумму S , возврат CashBack в виде бонусных баллов на счет карты.

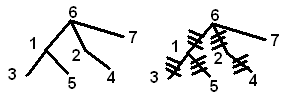
Сетевой график получения кредитной истории

1 — устройство на работу с трудовой книжкой; 2 , 3 — получение кредитной карты с минимальным кредитным лимитом. Некоторые банки выдают кредиты уже после 3 -х месячного трудового стажа, другие банки устанавливают этот срок от 1 года; 4 , 5 — продвинутый уровень , получение кредитных карт с большим cashback-ом; 6 — хорошая кредитная история, полученная с выгодой от использования кредитных карт.

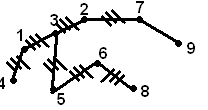
Схема транспортной сети

На схеме показаны взаимное расположение пунктов, длинны звеньев, потребность грузов в развозочной системе.

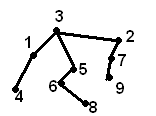
Задача календарного планирования с заданной технологией

Здесь показан пример ориентированного графа

Схема канала распределения

Товар после изготовления поступает в оптовую продажу, далее доходит либо до потребителя, либо следует в розничную продажу, а затем уже к потребителю. По данной схеме работают и продуктовые рынки.

Еще один пример построения схемы классификации аннуитетных платежей можно посмотреть здесь.

Видеоинструкция

Инструкция к сервису по рисованию графа

Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить . Если название вершины не задано, будет показан ее номер. По умолчанию, нумерация начинается с номера 1 . Чтобы нумерация начиналась с 0 , необходимо снять отметку с пункта Нумерация вершин с №1 . Название вершины может содержать символьную строку (перенос строк осуществляется через символ | ).
Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить . Если выбрана одна вершина, то будет создана петля. У выбранных элементов (вершин или дуг) можно изменить свойства или удалить их.

Основные определения

В математической теории графов и информатике граф представляет собой совокупность объектов со связями между ними. Граф G задается множеством точек (вершин) X=1,…,x_n> и множеством линий (ребер) A=1,…,a_m> , соединяющих между собой все или часть этих точек. На данный момент в сервисе для графического отображения вершин используются следующие фигуры: круг, квадрат и треугольник. Каждая вершина может иметь собственный вид: цвет и толщина линии, фон и размеры . Для изменения характеристик вершины необходимо выделить ее левой кнопки мыши и нажать на кнопку Свойства .

Ребра графа – линии, соединяющие вершины. Чтобы соединить вершины, необходимо выбрать одну или две из них. Каждое ребро графа имеет собственные свойства: цвет и толщина линии, значение (отображается поверх ребра).

Ребро графа называется неориентированным, если порядок расположения его концов (направление стрелок) в графе не принимается во внимание. Ребро графа называется ориентированным, если этот порядок существенен. Ориентированное ребро называют также дугой графа. Две вершины, соединённые дугой или ребром называются смежными. Для задания дуги необходимо при соединении вершин отметить пункт концевой маркер → . Для изменения типа дуги необходимо выделить ее левой кнопки мыши и нажать на кнопку Свойства .

С каждым ребром можно связать число или символ — вес ребра. Для задачи коммивояжера это может быть расстояние между городами, а для транспортной сети — стоимость проезда. Такой граф называется взвешенным.

Для каждого графа G(Х) существует обратный граф G -1 (Х) , полученный изменением ориентации каждого из ребер графа G(Х) на противоположную.

Петлей называется ребро g(x_i,x_i) , у которого начальная и конечная вершины совпадают. Петля обычно считается неориентированной. Для создания петли необходимо выделить только одну вершину и нажать на кнопку Соединить .

Ребра ориентированного графа с одинаковыми весами могут быть представлены в разном виде. Для настройки отображения используйте пункт Дуги с одинаковыми весами .

В неизменном виде: отображается каждая дуга с весом.

Источник

Коды Прюфера

Кодирование Прюфера переводит помеченные деревья порядка [math]n[/math] в последовательность чисел от [math]1[/math] до [math]n[/math] по алгоритму:
Пока количество вершин больше двух:

1. Выбирается лист [math]v[/math] с минимальным номером.
2. В код Прюфера добавляется номер вершины, смежной с [math]v[/math] .
3. Вершина [math]v[/math] и инцидентное ей ребро удаляются из дерева.

Полученная последовательность называется кодом Прюфера (англ. Prüfer code) для заданного дерева.

Номер вершины [math]v[/math] встречается в коде Прюфера тогда и только тогда, когда [math]v[/math] не является листом, причём встречается этот номер к коде дерева в точности [math]\deg v — 1[/math] раз.

1. Вершина с номером [math]n[/math] не может быть удалена, следовательно на последнем шаге у неё была смежная вершина, и число [math]n[/math] встретилось в коде.
2. Если вершина не является листом, то у неё на некотором шаге была смежная вершина [math]-[/math] лист, следовательно номер этой вершины встречается в коде.
3. Если вершина является листом с номером меньше [math]n[/math] , то она была удалена до того, как был удален её сосед, следовательно её номер не встречается в коде.

По любой последовательности длины [math]n — 2[/math] из чисел от [math]1[/math] до [math]n[/math] можно построить помеченное дерево, для которого эта последовательность является кодом Прюфера.

Доказательство проведем по индукции по числу [math]n[/math]
База индукции:

[math]n = 1[/math] [math]-[/math] верно.

Пусть для числа [math]n[/math] верно, построим доказательство для [math]n+1[/math] :

Пусть у нас есть последовательность: [math]A = [a_1, a_2, . a_].[/math]

Кодирование Прюфера задаёт биекцию между множествами помеченных деревьев порядка [math]n[/math] и последовательностями длиной [math]n — 2[/math] из чисел от [math]1[/math] до [math]n[/math]

Следствием из этой теоремы является формула Кэли.

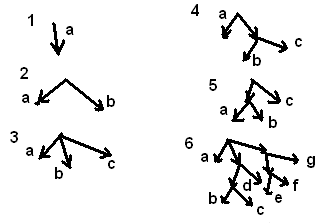
Пример построения кода Прюфера

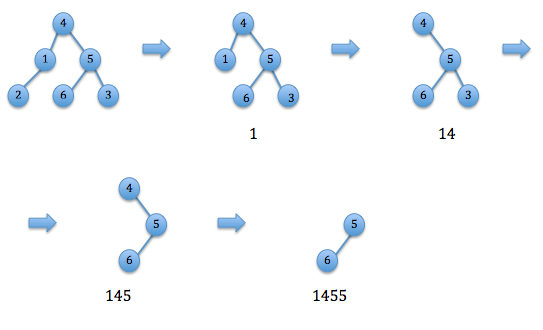
Алгоритм декодирования кодa Прюфера

В массиве вершин исходного дерева [math]V[/math] найдём вершину [math]v_[/math] с минимальным номером, не содержащуюся в массиве с кодом Прюфера [math]P[/math] , т.е. такую, что она является листом или концом уже добавленного в граф ребра, т.е. она стала листом в процессе построения кода Прюфера (по первому пункту построения). Вершина [math]p_1[/math] была добавлена в код Прюфера как инцидентная листу с минимальным номером (по второму пункту построения), поэтому в исходном дереве существует ребро < [math]p_1[/math] , [math]v_[/math] >, добавим его в список ребер. Удалим первый элемент из массива [math]Р[/math] , а вершину [math]v_[/math] — из массива [math]V[/math] т.к. она больше не может являться листом (по третьему пункту построения). Будем выполнять вышеуказанные действия, пока массив [math]P[/math] не станет пустым. В конце работы алгоритма в массиве [math]V[/math] останутся две вершины, составляющие последнее ребро дерева (это следует из построения).

Реализация

# P - код Прюфера # V - вершины function buildTree(P, V): while not P.empty(): u = P[0] v = min(x [math]\in[/math] V: P.count(x) == 0) G.push() P.erase(0) V.erase(indexOf(v)) G.push() return G

Пример декодирования кода Прюфера

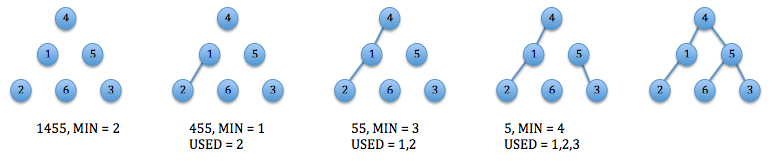
См. также

Источник

3.5. Код Прюфера.

Немецкий математик К.Прюфер изобрёл способ представления любых деревьев и ордеревьев. Изложим алгоритм построения кода Прюфера.

Пусть имеется дерево с n пронумерованными вершинами. В списке всех вершин слева направо ищем первую висячую вершину. Пусть это a_1. Ищем единственную вершину b₁ с которой смежна a₁. Величину b₁ заносим в новый список – будущий код Прюфера, а вершину a₁ вычеркиваем и из списка, и из дерева. Этот процесс повторяем n-2 раза. В результате получим новый список. 1, b₂,…, b_n-2> – это и есть код Прюфера. Заметим, что в процессе построения дерево все время уменьшается, и возникают новые висячие вершины

Построить код Прюфера для дерева.

В этом списке слева направо ищем первую висячую.

Доказано, что код Прюфера определяет дерево однозначно. Более того, любой список < b₁, b₂. b_n-2> чисел от 1 до n является кодом Прюфера некоторого дерева.

Восстановить дерево по коду Прюфера.

Введем понятие неприкосновенной вершины: если вершина встречается в коде Прюфера дальше, то она неприкосновенна

Д обавляем оставшиеся вершины.

Общее число деревьев с n пронумерованными вершинами равно n n -2 /

Таких деревьев ровно столько, сколько кодов Прюфера. b – число от 1 до n.

По правилу произведения n n-2

Например, для n=5, получим 5 5-2 =152 раз.

3.6. Обход деревьев.

Часто необходимо обойти все вершины дерева или ордерева не хаотично, а по определённому алгоритму.

Самые простые алгоритмы обхода для бинарного ордерева. Из 3 на выбор.

1)Прямой метод – обойти корень, затем левое поддерево, затем правое (КЛП)

Этот принцип соблюдается в любой момент времени.

2)Обратный метод: обойти левое поддерево, корень, правое поддерево (ЛКП)

3)Концевой метод: обойти левое поддерево, правое, корень (ЛПК)

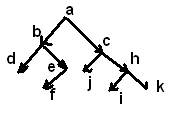
Обойти 3 способам данное бинарное дерево (не менее 10 вершин)

1 ) Прямой (КЛП) a b d e f c g h I k

2) Обратный (ЛКП) d b f e a g c I h k

3) Концевой (ЛПК) d f e b g I k h c a

Для не бинарных деревьев и ордеревьев алгоритм гораздо сложнее.

3.7. Деревья и списки.

Бытовое понятие списков всем известно, но в информатике имеется формальное понятие списка.

Опр. Назовем атомом любой неделимый объект (букву, цифру и т.д.). Списками называется последовательность атомов и списков, разделенных запятыми и заключенными в общие скобки.

Это так называемая рекурсивное определение (использующие само себя). В математике это запрещается, а информатике широко применяется.

Каждому списку можно сопоставить ордерево, действуя по правилу

Атомом или списком, заключенным в общие скобки, соответствует общая безымянная вершина, потомками которой они являются.

П ример.

Видим, что атомам соответствуют только висячие вершины дерева. Поэтому обратная связь такова: каждому дереву соответствует список его висячих вершин.

Вводится понятие глубины списка: наибольшее число вложенных друг в друга скобок.

При этом глубина списка совпадает с глубиной соответствующего дерева (число уровней).

Источник