Найти минимальное дерево графа

Минимальное остовное дерево (алгоритм Прима) онлайн калькулятор

Минимальное остовное дерево (алгоритм Прима)онлайн калькулятор
—>

Алгоритм Прима принимает квадратную матрицу (представляющую собой граф с взвешенными дугами) и находит дуги, которые образуют минимального остов . .

Вы можете повторно ввести значения (возможно, вам необходимо изменить симметричные значения вручную) и повторно вычислить решение. Программа не работает, если минимальное покрывающее дерево имеет вес более одного миллиарда . Эта реализация всегда начинает расчет с строки 1. Используемые дуги выделены красным цветом.
Если граф не связный остовное дерево будет найдено (но некоторые дуги могут быть выделены ).
Если граф связный , то используемые дуги буду выделены, а общий вес будет рассчитан.

Описание

1.введите размерность матрицы
2.заполните матрицу инцидентности для вашего графа
3.нажмите»запустить Prim»
4.выделите на вашемграфе нужные дуги входящие в остновное дерево, проверьте общий вес
пример расчета и преобразования графа в матрицу на картинке ниже

В информатике , Алгоритм Прима (также известный как Алгоритм Ярник ) является жадный алгоритмом , который находит минимальное остовное дерево для взвешенного неориентированного графа . Это означает, что он находит подмножество ребер, которое формирует дерево , включающее каждую вершину , где общий вес всех ребер в дереве минимизирован. Алгоритм строит это дерево по одной вершине за раз, из произвольной начальной вершины, на каждом шаге добавляя самое дешевое возможное соединение из дерева в другую вершину. Алгоритм был разработан в 1930 году чешским математиком Войтехом Ярником , а затем переоткрыт и переиздан компьютерными учеными Робертом К. Примом в 1957 году и Эдсгером В. Дейкстрой в 1959 году Поэтому его также иногда называют Алгоритмом Ярника , Алгоритмом Прима – Ярника , Алгоритмом Прима – Дейкстры или Алгоритмом DJP .

Источник

Алгоритм Краскала, Прима для нахождения минимального остовного дерева

Алгоритмы нахождения MST применимы в различных областях, начиная от кластеризации данных до построения компьютерных, транспортных сетей.
Я надеюсь, что вы после прочтения данной статьи, примерно понимали, как работают жадные алгоритмы нахождения MST.

Формальная постановка задачи

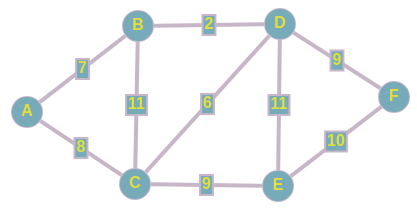
Имеется следующий неориентированный взвешенный граф. Назовем остовным деревом подграф, содержащий все вершины исходного графа, который является деревом. И задача состоит в том, чтобы найти такое остовное дерево, сумма рёбер которого минимальна.

Неформальная постановка задачи

Представьте исходный граф без рёбер, теперь вам нужно как-то соединить все вершины между собой, чтобы можно было бы попасть из любой вершины в другую, не имея при этом циклов в получившемся графе с минимально возможной суммой весов включенных рёбер.

Алгоритм Краскала

Механизм, по которому работает данный алгоритм, очень прост. На входе имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева. Будем рассматривать только связные графы, в другом случае при применении алгоритма Краскала мы будем получать не минимальное остовное дерево, а просто остовной лес.

• Вначале мы производим сортировку рёбер по неубыванию по их весам.
• Добавляем i-ое ребро в наш подграф только в том случае, если данное ребро соединяет две разные компоненты связности, одним из которых является наш подграф. То есть, на каждом шаге добавляется минимальное по весу ребро, один конец которого содержится в нашем подграфе, а другой — еще нет.
• Алгоритм завершит свою работу после того, как множество вершин нашего подграфа совпадет с множеством вершин исходного графа.

Данный алгоритм называется жадным из-за того, что мы на каждом шаге пытаемся найти оптимальный вариант, который приведет к оптимальному решению в целом.

Разбор конкретного примера по шагам

Из представленного сверху графа, выпишем все его ребра в отсортированном порядке:

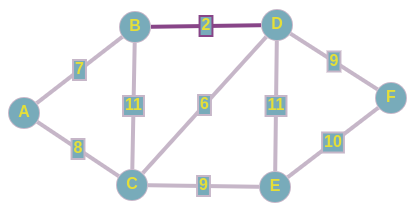
1) D B; w = 2
2) D C; w = 6
3) A B; w = 7
4) A C; w = 8
5) C E; w = 9
6) D F; w = 9
7) F E; w = 10
8) B C; w = 11
9) D E; w = 11

И начнем по списку добавлять эти ребра в наш остов:

При добавлении в наше остовное дерево ребра A C, как вы можете заметить, образовывается цикл, поэтому мы просто пропускаем данное ребро.

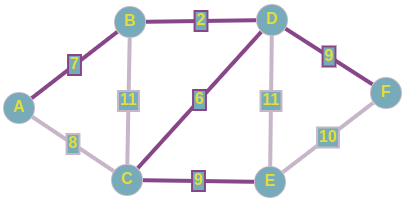
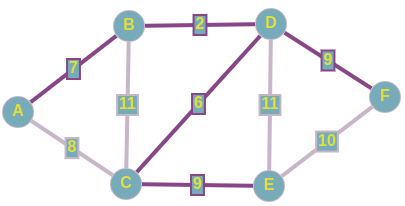
По итогу у нас образовывается следующий подграф, и как вы заметили, мы соединили все вершины ребрами с минимально-возможными весами, а значит, нашли минимальное остовное дерево для нашего исходного графа.

Проводим проверку с помощью встроенного алгоритма для нахождения MST на graphonline, и видим, что подграфы идентичны.
И да, из-за того, что при равенстве весов рёбер мы можем выбрать любое из них, конечные подграфы, являющиеся минимальными остовными деревьями, могут различаться с точностью до некоторых рёбер.

Суммарный вес искомого MST равен 33.

Реализация

Реализовать представленный алгоритм проще всего с помощью СНМ(система непересекающихся отрезков).

Вначале, как мы уже раннее говорили, необходимо отсортировать ребра по неубыванию по их весам. Далее с помощью вызовов функции make_set() мы каждую вершину можем поместить в свое собственное дерево, то есть, создаем некоторое множество подграфов. Дальше итерируемся по всем ребрам в отсортированном порядке и смотрим, принадлежат ли инцидентные вершины текущего ребра разным подграфам с помощью функции find_set() или нет, если оба конца лежат в разных компонентах, то объединяем два разных подграфа в один с помощью функции union_sets().

В итоге асимптотическая сложность данного алгоритма сводится к:

, где:
sort() —
make_set()-
find_set —
union_sets —

vector parent, rank; void make_set(int v) < parent[v] = v; rank[v] = 0; >int find_set(int v) < if (v == parent[v]) return v; return parent[v] = find_set(parent[v]); >void union_sets(int a, int b) < a = find_set(a); b = find_set(b); if (a != b) < if (rank[a] < rank[b]) swap(a, b); parent[b] = a; if (rank[a] == rank[b]) rank[a]++; >> struct Edge < int u, v, weight; bool operator<(Edge const& other) < return weight < other.weight; >>; int n; vector edges; int cost = 0; vector result; parent.resize(n); rank.resize(n); for (int i = 0; i < n; i++) make_set(i); sort(edges.begin(), edges.end()); for (Edge e : edges) < if (find_set(e.u) != find_set(e.v)) < cost += e.weight; result.push_back(e); union_sets(e.u, e.v); >>

Алгоритм Прима

Суть самого алгоритма Прима тоже сводится к жадному перебору рёбер, но уже из определенного множества. На входе так же имеется пустой подграф, который и будем достраивать до потенциального минимального остовного дерева.

• Изначально наш подграф состоит из одной любой вершины исходного графа.
• Затем из рёбер инцидентных этой вершине, выбирается такое минимальное ребро, которое связала бы две абсолютно разные компоненты связности, одной из которых и является наш подграф. То есть, как только у нас появляется возможность добавить новую вершину в наш подграф, мы тут же включаем ее по минимальмально возможному весу.
• Продолжаем выполнять предыдущий шаг до тех пор, пока не найдем искомое MST.

Разбор конкретного примера

Выбираем чисто случайно вершину E, далее рассмотрим все ребра исходящие из нее, включаем в наше остовное дерево ребро C E; w = 9, так как данное ребро имеет минимальный вес из всех рёбер инцидентных множеству вершин нашего подграфа. Имеем следующее:

Теперь выборка производится из рёбер:
D C; w = 6
A C; w = 8
F E; w = 10
B C; w = 11
D E; w = 11

То есть, в данный момент, мы знаем только о двух вершинах, соответственно, знаем о всех ребрах, исходящих из них. Про связи между другими вершинами, которые не включены в наш подграф, мы ничего не знаем, поэтому они на этом шаге не рассматриваются.

Добавляем в наш подграф ребро D C и по аналогии добаляем ребро D B . Получаем следующее:

Давайте добьем наш подграф до минимального остовного дерева. Вы, наверное, уже догадались о том, по каким ребрам мы будем связывать наши оставшиеся вершины:
A и F.

Проводим последние штрихи и получили тот же самый подграф в качестве минимального остовного дерева. Но как мы раннее говорили, сам подграф ничего не решает, главное тут — множество рёбер, которые включены в наше остовное дерево.

Суммарный вес искомого MST равен 33.

Источник

Минимальное остовное дерево. Алгоритм Прима. Алгоритм Крускала

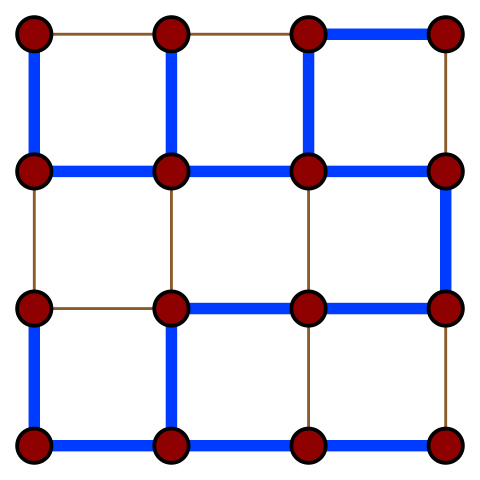
Остовным деревом графа называется дерево, которое можно получить из него путём удаления некоторых рёбер. У графа может существовать несколько остовных деревьев, и чаще всех их достаточно много.

На иллюстрации приведено одно из остовных деревьев (рёбра выделены синим цветом) решёткообразного графа.

Для взвешенных графов существует понятие веса остовного дерева, которое определено как сумма весов всех рёбер, входящих в остовное дерево. Из него натурально вытекает понятие минимального остовного дерева — остовного дерева с минимальным возможным весом.

Для нахождения минимального остовного дерева графа существуют два основных алгоритма: алгоритм Прима и алгоритм Крускала. Они оба имеют сложность \(O(M \log N)\), поэтому выбор одного из них зависит от ваших личных предпочтений. В этой лекции мы разберём оба.

Алгоритм Прима

Алгоритм Прима в идее и реализации очень похож на алгоритм Дейкстры. Как и в алгоритме Дейкстры, мы поддерживаем уже обработанную часть графа (минимального остовного дерева), и постепенно её расширяем за счёт ближайших вершин.

Утверждается, что если разделить вершины графа на два множества (обработанные и необработанные), первое из которых составляет связную часть минимального остовного дерева, то ребро минимальной длины, связывающее эти два множества гарантированно будет входить в минимальное остовное дерево.

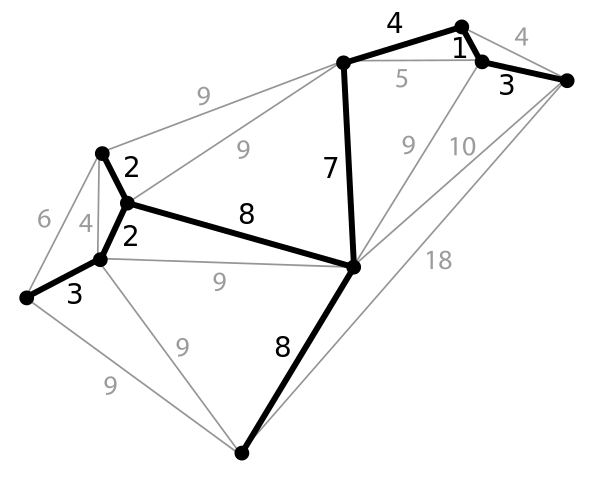
Таким образом, для нахождения минимального остовного дерева начнём с произвольной вершины и будем постепенно добавлять ближайшие к уже имеющимся.

На иллюстрации красным цветом выделены рёбра, уже вошедшие в минимальный остов, а чёрным — текущие кандидаты, из которых выбирается ребро с минимальным весом.

Реализация алгоритма Прима

Будем искать вес минимального остовного дерева. Для нахождения ближайшей вершины воспользуемся очередью с приоритетом (аналогично алгоритму Дейкстры), в которой будем хранить пары (расстояние от остова до вершины, номер вершины).

Различия в скорости работы

Хотя оба алгоритма работают за \(O(M \log N)\), существуют константные различия в скорости их работы. На разреженных графах (количество рёбер примерно равно количеству вершин) быстрее работает алгоритм Крускала, а на насыщенных (количество рёбер примерно равно квадрату количеству вершин) — алгоритм Прима (при использовании матрицы смежности).

На практике чаще используется алгоритм Крускала.

brestprog

Олимпиадное программирование в Бресте и Беларуси

Источник