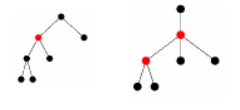
Алгоритмы на деревьях
Пусть дан граф [math]G = \langle V, E \rangle [/math] . Тогда диаметром [math]d[/math] называется [math]\max\limits_ dist(v, u)[/math] , где [math]dist[/math] — кратчайшее расстояние между вершинами.
Алгоритм
- Возьмём любую вершину [math] v \in V [/math] и найдём расстояния до всех других вершин. [math]d[i] = dist(v, i)[/math]
- Возьмём вершину [math] u \in V [/math] такую, что [math]d[u] \geqslant d[t][/math] для любого [math]t[/math] . Снова найдём расстояние от [math]u[/math] до всех остальных вершин. Самое большое расстояние — диаметр дерева.
Расстояние до остальных вершин будем искать алгоритмом [math]BFS[/math] .
Реализация
//граф g представлен списком смежности int diameterTree(list> g): v = u = w = 0 d = bfs(g, v) for i = 0, i < n, i++ if d[i] > d[u] u = i d = bfs(g, u) for i = 0, i < n, i++ if d[i] > d[w] w = i return d[w] Обоснование корректности
Будем пользоваться свойством, что в любом дереве больше одного листа. Исключительный случай — дерево из одной вершины, но алгоритм сработает верно и в этом случае.
После запуска алгоритма получим дерево [math]BFS[/math] .
В дереве [math]BFS[/math] не существует ребер между вершинами из разных поддеревьев некоторого их общего предка.
Предположим, существует ребро [math]u, v[/math] между соседними поддеревьями:
Мы свели задачу к нахождению вершины [math]w[/math] , такой что сумма глубин поддеревьев максимальна.
Докажем, что одно из искомых поддеревьев содержит самый глубокий лист. Пусть нет, тогда, взяв расстояние от [math]w[/math] до глубочайшего листа, мы можем улучшить ответ.
Таким образом мы доказали, что нам нужно взять вершину [math]u[/math] с наибольшей глубиной после первого [math]BFS[/math] , очевидно, что ей в пару надо сопоставить вершину [math]w[/math] , такую что [math]dist(u, w)[/math] максимально. Вершину [math]w[/math] можно найти запуском [math]BFS[/math] из [math]u[/math] .
Оценка времени работы
Все операции кроме [math]BFS[/math] — [math]O(1)[/math] . [math]BFS[/math] работает за линейное время, запускаем мы его два раза. Получаем [math]O(|V| + |E|)[/math] .
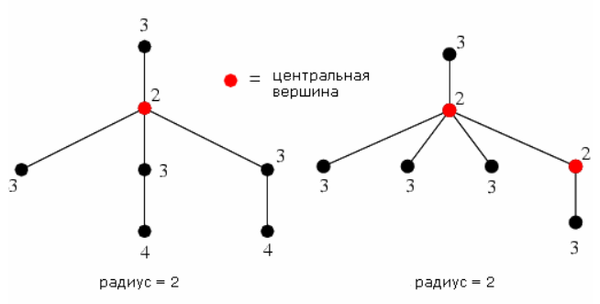
Центр дерева
Определения
| Определение: |
| Эксцентриситет вершины [math]e(v)[/math] (англ. eccentricity of a vertex) — [math]\max\limits_ |
| Определение: |
| Радиус [math]r(G)[/math] (англ. radius) — наименьший из эксцентриситетов вершин графа [math]G[/math] . |
| Определение: |
| Центральная вершина (англ. central vertex) — вершина графа [math]G[/math] , такая что [math]e(v) = r(G)[/math] |
| Определение: |
| Центр графа [math]G[/math] (англ. center of a graph) — множество всех центральных вершин графа [math]G[/math] . |
Алгоритм
Наивный алгоритм
Найдём центр графа исходя из его определения.
- Построим матрицу [math]A_[/math] ( [math]n[/math] — мощность множества [math]V[/math] ), где [math]a_ = d_[/math] , то есть матрицу кратчайших путей. Для её построения можно воспользоваться алгоритмом Флойда-Уоршелла или Дейкстры.
- Подсчитаем максимум в каждой строчке матрицы [math]A[/math] . Таким образом, получим массив длины [math]n[/math] .
- Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами.
Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет [math]O(V^3)[/math] , а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и [math]O(V^2)[/math] , за которую мы находим максимумы в матрице.
Алгоритм для дерева за O(n)
Собственно, алгоритм нахождения центра описан в доказательстве теоремы.
- Пройдёмся по дереву обходом в глубину и пометим все висячие вершины числом [math]0[/math] .
- Обрежем помеченные вершины.
- Образовавшиеся листья пометим числом [math]1[/math] и тоже обрежем.
- Будем повторять, пока на текущей глубине не окажется не более двух листьев, и при этом в дереве будет тоже не более двух листьев.
Оставшиеся листья являются центром дерева.
Для того, чтобы алгоритм работал за [math]O(n)[/math] , нужно обрабатывать листья по одному, поддерживая в очереди два последовательных по глубине слоя.
См. также
Источники информации
Источник
§ 12. Центры дерева
Пусть каждое ребро графа G имеет единичную длину. Длина цепи, соединяющей вершины v и u , в этом случае, равна числу ребер этой цепи. Пусть v – некоторая вершина дерева G, от которой можно прийти к любой другой вершине u , при этом длину цепи обозначим через d(v,u) . Максимальное из этих величин d(v,u) по всевозможным u G называется эксцентриситетом вершины v и обозначается как е ( v ) . Итак, эксцентриситет вершины v равен числу е ( v ) = max d(v,u) . На рис. 5.23, а) приведён граф u G (дерево), для вершин v и u которого, очевидно, имеем: е ( v ) = 3, е ( u ) = 2. Наибольший из эксцентриситетов вершин
150 графа G называется диаметром графа G, который обозначают d(G), d(G)= max d(v,u) . Таким образом, диаметр графа G равен длине наибольшей v ,u G простой цепи графа. Радиусом r(G) называется наименьший из эксцентриситетов вершин графа G : r(G) = = min e(u) . u G Вершина v называется центральной вершиной графа G , если e(v)= r(G). Центр графа G – это множество всех центральных вершин. На рис. 5.23, б) построен граф, для которого d(G)= 7 , r(G)= 4 , а центр состоит из двух вершин v и u. Теорема 5.14. Каждое дерево имеет центр, состоящий или из одной вершины, или из двух смежных вершин. Доказательство. Утверждение очевидно для 1 и 2-х вершинных графов. Покажем, что у любого дерева Т те же центральные вершины, что и у дерева Т ’ , полученного из Т удалением всех его висячих вершин. Ясно, что расстояние от данной вершины v любого дерева Т до любой другой вершины u может достигать наибольшего значения только тогда, когда u – висячая вершина. Таким образом, эксцентриситет каждой оставшейся в Т ’ вершине точно на единицу меньше эксцентриситета этой же вершины в Т . Отсюда следует, что вершины дерева Т , имеющие наименьший эксцентриситет в Т , совпадают с вершинами, имеющими наименьший эксцентриситет в Т ’ , т.е. центры деревьев Т и Т ’ совпадают. Если процесс удаления висячих вершин продолжить, то получим последовательность деревьев с тем же центром, что и у дерева Т . В силу конечности Т обязательно придем к 1 или 2 — х вершинному дереву. В любом случае все вершины дерева, полученного таким образом, образуют центры дерева Т , и этот центр состоит или из единственной вершины, или из двух смежных вершин. Зри в корень . К . Прутков
§ 13. Ориентированные деревья
Ориентированным деревом (или ордеревом , или корневым деревом ) называется орграф со следующими свойствами: 1) существует единственная вершина, полустепень захода которой равна 0. Она называется корнем ордерева; 2) полустепень захода всех остальных вершин равна 1; 3) каждая вершина достижима из корня. На рис. 5.24 приведены всевозможные ордеревья с тремя (рис 5.24, а) и с четырьмя (рис 5.24, б) вершинами.
151
| а) | б) |
Рис. 5.24 Пусть, как обычно, n – число вершин, а m – число дуг орграфа. Теорема 5.15. Ордерево обладает следующими свойствами: 1) m = n – 1; 2) если в ордереве отменить ориентацию ребер, то получится дерево; 3) в ордереве нет контуров; 4) для каждой вершины существует единственный путь, ведущий в эту вершину из корня; 5) подграф, определяемый множеством вершин, достижимых из некоторой вершины v данного ордерева, является ордеревом с корнем v (это ордерево называется поддеревом вершины v ); 6) если в свободном дереве любую вершину назначить корнем и ввести ориентацию ребер от корня к концевым вершинам, то получится ордерево. Доказательство : 1. Каждая вершина достижима из корня и полустепени захода всех вершин кроме корневой вершины, равны единице, следовательно, m = n — 1. 2. Пусть G – ордерево, граф G ′ получен из G отменой ориентации ребер, u – корень. Тогда для v 1 ,v 2 V существуют цепи Z(v 1 ,u) и Z(u,v 2 ) в графе G ′ , поэтому любые две вершины v 1 , v 2 V соединены цепью Z(v 1 ,v 2 )= Z(v 1 ,u) Z(u,v 2 ), следовательно, граф G ′ связен. Допустим, что G ′ содержит цикл С и v 1 , v 2 различные вершины этого цикла. Тогда, кроме цепи Z(v 1 ,v 2 )= Z(v 1 ,u) Z(u,v 2 ), должна быть другая цепь Z*(v 1 ,v 2 ), соединяющая вершины v 1 и v 2 . Следовательно, в графе G одна из вершин v 1 или v 2 должна иметь полустепень захода больше чем единица, что не может быть. Таким образом, допущение неверно и G ′ не имеет циклов, т.е. G ′ — дерево. 3. Следует из 2. 4. От противного. Если бы в G существовали два пути из u в v , то в G ′ имелся бы цикл. Утверждения 5) и 6) теоремы 5.15 оставляем читателю в качестве упражнений. Концевая вершина ордерева называется листом . Путь из корня в лист называется ветвью . Длина наибольшей ветви ордерева называется высотой
§ 14. Эйлеровы графы
153 которого изображена на рис. 5.25. Эйлер показал, что этот граф не представляет единого цикла. Ибо если бы он существовал, то в каждой вершине графа было бы столько же входящих в нее ребер, сколько и выходящих из нее, т.е. в каждой вершине графа было бы четное число ребер. Таким образом, из какой бы вершины не начинался обход, обойти весь граф и вернуться обратно невозможно, не проходя никакого ребра дважды. Изложив решение задачи о кенигсбергских мостах, Эйлер в своей работе перешел к следующей общей проблеме теории графов: на каких графах можно найти цикл С , содержащий все ребра графа, причем каждое ребро в точности по одному разу? Такой цикл, т.е. цикл, содержащий все ребра графа в точности по одному разу, называется эйлеровым циклом , а граф, обладающий эйлеровым циклом – эйлеровым графом . Теорема 5.17. Конечный граф G является эйлеровым графом тогда и только тогда, когда: 1) G связен; 2) все его локальные степени четны. Доказательство. Необходимость условия 1) очевидна. Далее, каждый раз, когда эйлеров цикл проходит через какую-то вершину, он должен войти в нее по одному ребру и выйти по другому, поэтому условие 2) также необходимо. Достаточность. Пусть условие 1) и 2) выполняется. Докажем, что граф эйлеров. Начнем цепь С в произвольной вершине v графа G и будем продолжать ее, насколько возможно, все время через новые ребра. Так как в каждой вершине число ребер четно, этот процесс может закончиться только в v , следовательно, цепь С будет циклом. Если C проходит через все ребра графа G , то цикл построен. Если же C содержит не все ребра графа G , то удалим из G ребра этого цикла С , в результате получим подграф G* . Графы С и G имеют четные локальные степени, следовательно, то же должно быть справедливо и для G* . Так как граф G связный, в C должна существовать вершина u , инцидентная ребрам из G*, см. рис. 5.26. Из вершины u можно построить новую цепь С * , содержащую ребра только из G*, и такая цепь может закончиться только при возвращении в u . Пусть S(v,u) и S(v,u) две
| цепи, из которых образован цикл С . | |||||
| v | Тогда можно составить новый цикл: | ||||
| u | который | ||||
| С 1 =S(v,u) | С * | S(v,u), | |||
| возвращается в v и содержит больше | |||||
| ребер, чем С , см. рис. 5.26, где цикл С | |||||
| изображен сплошной линией, а цикл | |||||
| С * – штриховой. Если С 1 не является | |||||
| Рис. 5.26 | эйлеровым циклом, то это построение | ||||
| повторяется. | Когда | процесс | |||
закончится, эйлеров цикл будет построен. Теорема доказана.
154 Доказательство теоремы даёт и алгоритм нахождения эйлерового цикла. Для нахождения эйлерового цикла можно построить алгоритм в следующем виде: Алгоритм построения эйлерового цикла: Вход: эйлеров граф G(V,X), заданный списками смежности ( L [ v ] – список вершин, смежных с вершиной v ). Выход: последовательность вершин эйлерова цикла. S := <стек для хранения вершин>select v V v → S while S ≠ do v ← S ; v → S < v - верхний элемент стека>if L [ v ] = then v ← S ; yield v else select u L [ v ] u → S L [ v ]:= L [ v ]\ < u >; L [ u ]:= L [ u ]\ < v > end if end while Можно поставить аналогичную задачу для отыскания цепи, начинающейся в некоторой вершине v и заканчивающейся в другой вершине u , причем содержащей каждое ребро один и только один раз. Теорема 5.18. Для того чтобы на связном графе имелась цепь S(v,u) , содержащая все его ребра в точности по одному разу, необходимо и достаточно, чтобы v и u были единственными вершинами нечетной степени для этого графа. Доказательство. Необходимость. Пусть имеется цепь S(v,u), проходящая по всем ребрам в точности по одному разу. Эта цепь начинается в вершине v , возможно, в дальнейшем снова заходит в v , и далее не один раз. Если цепь не заканчивается в v, то эта вершина должна иметь нечетную степень. Аналогично и для u , в то время как все остальные вершины графа должны быть четны. Достаточность. Пусть v и u — единственные вершины с нечётной степенью. Добавим к графу G ребро (v,u) , тогда все вершины будут иметь четную степень и согласно теореме 5.17 граф обладает эйлеровым циклом; если из этого цикла удалить ребро (v,u), останется искомая цепь S(v,u) . Что и требовалось доказать.
Источник