Нечеткое дерево принятия решений

Построение нечёткого дерева решений

В данном разделе необходимо построить нечеткое дерево решений, с помощью которого определить рейтинг выбора места организации магазина, который посещают 50 000 тысяч человек за месяц и расстояние до базы 40 км.

В таблице 1 представлены данные о семи местах организации магазина: проходимость (определена, исходя из оценок, выставляемых рейтинговым агентством), расстояние до базы (в километрах) и рейтинг (определен экспертом).

Табл. 1  данные о месте организации магазина

Определение лингвистических переменных

Т(х): «низкая», «средняя», «большая»;

G: «достаточно», «недостаточно»;

М: задано таблично (таблица 2).

G: «достаточно», «недостаточно»;

М: задано таблично (таблица 3).

Табл.2  Табличное представление семантического правила для х₁

Построение функций принадлежности

Общий вид функций принадлежности лингвистических переменных показан на рисунке 1.

Рис.1  Графики функции принадлежности

Расчёт e(sn), g(sn)

Необходимо найти значение общей энтропии:

Рассчитываем значение энтропии E(S N ), воспользовавшись формулой :

E(S N )= -3/7log₂3/7 – 4/7log₂4/7  0,985 бит

Рассчитаем E(S N , проходимость).

E(S N , проходимость, низкая):

Р_да низкая =min(0;1)+min(0;0,8)+min(0,3;0,5)+min(0,4;0,2)+min(0,5;0)+min(0,8;0)+min(1;0)=0+0+0,3+0,2+0+0+0=0,5

Р_нет низкая =min(1;1)+min(1;0,8)+min(0,7;0,5)+min(0,6;0,2)+min(0,5;0)+min(0,2;0)+ min (0;0)=1+0,8+0,5+0,2+0+0+0=2,5

E(проходимость, низкая)= — 0,5/3,0 log₂0,5/3,0-2,5/3,0 log₂2,5/3,0=0,65 бит

Рассчитаем E(S N , проходимость, средняя).

Р_да средняя =min(0;0)+min(0;0,2)+min(0,3;0,5)+min(0,4;0,8)+min(0,5;0,5)+min(0,8;0)+min(1;0)=0,3+0,4+0,5=1,2

Р_нет средняя = min(1;0)+min(1;0,2)+min(0,7;0,5)+min(0,6;0,8)+min(0,5;0,5)+min(0,2;0)+min(0;0)=0,2+0,5+0,6+0,5=1,8

E(проходимость, средняя)= — 1,2/3 log₂1,2/3-1,8/3 log₂1,8/3=0,97 бит

Рассчитаем E(S N , проходимость, большая).

Р_да большая =min(0;0)+min(0;0)+min(0,3;0)+min(0,4;0)+min(0,5;0,5)+min(0,8;1)+min(1;1)=0,5+0,8+1=2,3

Р_нет большая =min(1;0)+min(1;0)+min(0,7;0)+min(0,6;0)+min(0,5;0,5)+min(0,2;1)+min(0;1)=0,5+0,2=0,7

E(проходимость, большая)= — 2,3/3 log₂2,3 /3-0,7/3 log₂0,7/3=0,78 бит

Источник

Документация

Когда количество входных параметров к нечеткой системе увеличивается, количество правил увеличивается экспоненциально. Эта большая основа правила уменьшает вычислительный КПД нечеткой системы. Это также делает операцию нечеткой системы тяжелее, чтобы понять, и это делает настройку правила и параметров функции принадлежности более трудной. Поскольку много приложений имеют ограниченные суммы обучающих данных, большая основа правила уменьшает generalizability настроенных нечетких систем.

Чтобы преодолеть эту проблему, можно реализовать нечеткую систему вывода (FIS), когда дерево меньших соединило объекты FIS, а не как один монолитный объект FIS. Они fuzzy trees также известен как hierarchical fuzzy systems, потому что нечеткие системы располагаются в иерархических древовидных структурах. В древовидной структуре выходные параметры низкоуровневых нечетких систем используются в качестве входных параметров к высокоуровневым нечетким системам. Нечеткое дерево более в вычислительном отношении эффективно и легче понять, чем один FIS с тем же количеством входных параметров.

Типы иерархических структур

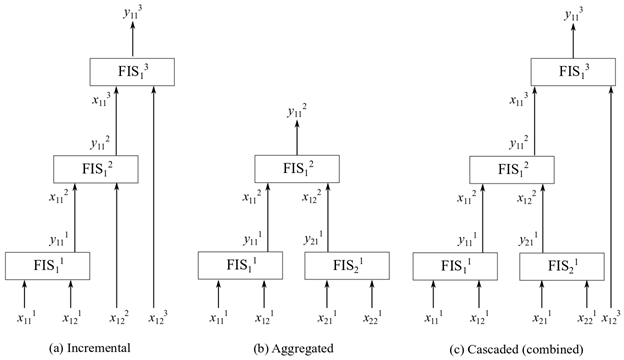
Существует несколько нечетких древовидных структур, которые можно использовать для приложения. Следующий рисунок показывает обычно используемые нечеткие древовидные структуры: инкрементная, агрегированная, или расположенная каскадом структура.

Инкрементная структура

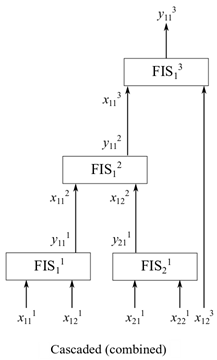
В инкрементной структуре входные значения включены в несколько этапов, чтобы совершенствовать выходные значения на нескольких уровнях. Например, предыдущий рисунок показывает трехуровневое инкрементное нечеткое дерево, имеющее нечеткие системы вывода F I S i n , где i указывает на индекс FIS в n th уровень. В инкрементном нечетком дереве, i = 1, означая, что каждый уровень имеет только одну нечеткую систему вывода. На предыдущем рисунке j th вход i th FIS в n th уровень показывается входом x i j n , тогда как k th выход i th FIS в n th уровень показывается входом x i k n . На рисунке, n = 3, j = 1 или 2, и k = 1. Если каждый вход имеет функции принадлежности m (MFS), каждый FIS имеет полный набор m 2 правила. Следовательно, общим количеством правил является nm 2 = 3 ⨉ 32 = 27 .

Следующий рисунок показывает монолитное (n = 1) FIS с четырьмя входными параметрами (j =1, 2, 3, 4) и три MFS (m = 3).

В FIS этого рисунка общим количеством правил является nm 4 = 1 ⨉ 34 = 81 . Следовательно, общее количество правил в инкрементном нечетком дереве линейно с количеством входных пар.

Введите выбор на разных уровнях в инкрементных нечетких входных рейтингах использования дерева на основе их вкладов в значения окончательного результата. Входные значения, которые способствуют больше всего, обычно используются на самом низком уровне, в то время как наименее влиятельные единицы используются на высшем уровне. Другими словами, входные значения низкого ранга зависят от входных значений высшего звания.

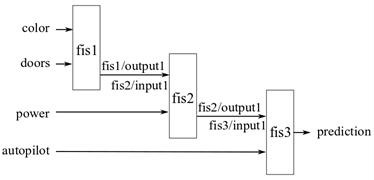
В инкрементном нечетком дереве каждое входное значение обычно способствует процессу вывода до некоторой степени, не значительно коррелируясь с другими входными параметрами. Например, нечеткая система предсказывает возможность покупки автомобиля с помощью четырех входных параметров: цвет, количество дверей, л.с. и автопилота. Входные параметры являются четырьмя отличными автомобильными функциями, которые могут независимо влиять на решение покупателя. Следовательно, входные параметры могут быть оценены с помощью существующих данных, чтобы создать нечеткое дерево как показано в следующем рисунке.

Для примера, который иллюстрирует создание инкрементного нечеткого дерева в MATLAB ® , смотрите, «Создают Инкрементный Древовидный» пример FIS на fistree страница с описанием.

Агрегированная структура

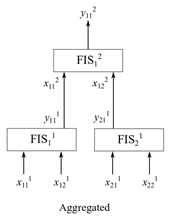
В агрегированной структуре входные значения включены как группы на самом низком уровне, где каждая входная группа подана в FIS. Выходные параметры более низкого уровня нечеткие системы объединены (агрегированное) использование высокоуровневых нечетких систем. Например, следующее показывает двухуровневое агрегированное нечеткое дерево, имеющее нечеткие системы вывода F I S i n n , где _in указывает на индекс FIS в n th уровень.

В этом агрегированном нечетком дереве, i ₁ = 1,2 и i ₂ = 1. Следовательно, каждый уровень включает различное количество FIS. j th вход _in th FIS показан на рисунке, как введено x i n j , и k th выход _in th FIS показывается, как выведено y i n k . На рисунке, j = 1,2 и k = 1. Другими словами, каждый FIS имеет два входных параметров и один выход. Если каждый вход имеет MFS m, то каждый FIS имеет полный набор m 2 правила. Следовательно, общее количество правил для трех нечетких систем является 3 m2 = 3 ⨉ 32 = 27, который совпадает с инкрементным FIS для подобной настройки.

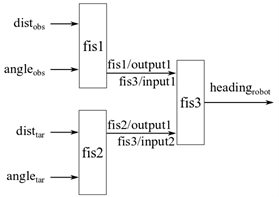
В агрегированном нечетком дереве входные значения естественно группируются для определенного принятия решений. Например, автономная задача навигации робота комбинирует предотвращение препятствия и целевые подзадачи достижения для навигации без коллизий. Чтобы достигнуть задачи навигации, нечеткое дерево может использовать четыре входных параметров: расстояние до самого близкого препятствия, угла самого близкого препятствия, расстояния до цели и угла цели. Расстояния и углы измеряются относительно текущего положения и направляющегося направления робота. В этом случае, на самом низком уровне, входные параметры естественно группа как показано в следующем рисунке: расстояние препятствия и угол препятствия (группа 1) и целевое расстояние и целевой угол (группа 2). Две нечетких системы отдельно входные параметры группы индивидуума процесса и затем другая нечеткая система комбинируют свои выходные параметры, чтобы произвести достижение без коллизий робота.

Для примера, который иллюстрирует создание агрегированного нечеткого дерева в MATLAB, смотрите, что пример Создает Агрегированное Дерево FIS на fistree страница с описанием.

Изменение на агрегированной структуре

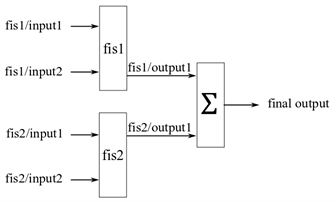
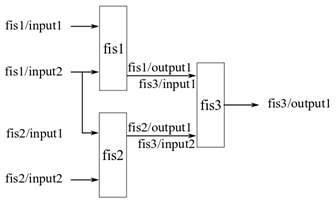
В изменении агрегированной структуры, известной как parallel structure [1], выходные параметры самого низкого уровня, нечеткие системы непосредственно суммированы, чтобы сгенерировать значение окончательного результата. Следующий рисунок показывает пример параллельного нечеткого дерева, где выходные параметры fis1 и fis2 суммированы, чтобы произвести окончательный результат.

fistree объект не обеспечивает узел подведения итогов Σ. Поэтому необходимо добавить пользовательский метод агрегации, чтобы оценить параллельное нечеткое дерево. Для примера смотрите, «Создают и Оценивают Параллельный пример» Дерева FIS на fistree страница с описанием.

Расположенная каскадом или объединенная структура

Каскадная структура, также известная как объединенную структуру, комбинирует и инкрементные и агрегированные структуры, чтобы создать нечеткое дерево. Эта структура подходит для системы, которая включает и коррелируемые и некоррелированые входные параметры. Древовидные группы коррелированые входные параметры в агрегированной структуре, и добавляют некоррелированые входные параметры в инкрементной структуре. Следующий рисунок показывает пример каскадной древовидной структуры, где первые четыре входных параметров сгруппированы попарно в агрегированной структуре, и пятый вход добавляется в инкрементной структуре.

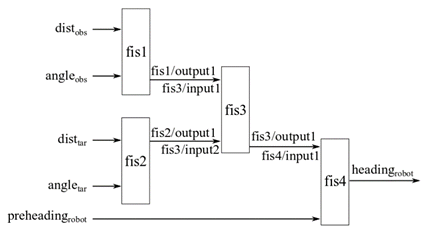
Например, считайте задачу навигации робота обсужденной в Агрегированной Структуре. Предположим, что задача включает другой вход, предыдущий заголовок робота, учтенного, чтобы предотвратить большие изменения в заголовке робота. Можно добавить этот вход с помощью инкрементной структуры следующей схемы.

Для примера, который иллюстрирует создание агрегированного нечеткого дерева в MATLAB, смотрите, «Создают Каскадный Древовидный» пример FIS на fistree страница с описанием.

Добавьте или удалите дерево FIS Выходные параметры

Когда вы оцениваете fistree объект, это возвращает результаты только для открытых выходных параметров, которые не соединяются ни с какими входными параметрами FIS в нечетком дереве. Можно опционально получить доступ к другим выходным параметрам в дереве. Например, в следующей схеме агрегированного нечеткого дерева, вы можете хотеть получить выход fis2, когда вы оцениваете дерево.

Можно добавить такие выходные параметры в fistree объект. Можно также удалить выходные параметры, при условии, что нечеткое дерево всегда имеет по крайней мере один выход. Для примера смотрите «Обновление Дерево FIS Выходные параметры» пример на fistree страница с описанием.

Используйте То же Значение для Нескольких входных параметров Дерева FIS

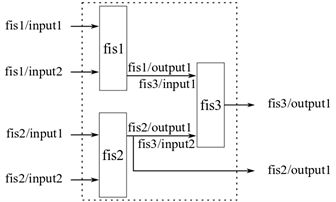
fistree объект позволяет использовать то же значение для нескольких входных параметров. Например, в следующем рисунке, input2 из fis1 и input1 из fis2 используйте то же значение во время оценки.

Для примера, показывающего, как создать дерево FIS таким образом, смотрите «Использование То же Значение для Нескольких Входных параметров Древовидного» примера FIS на fistree страница с описанием.

Обновите нечеткие системы вывода в дереве FIS

Можно добавить или удалить отдельные элементы FIS из fistree объект. Когда вы делаете так, программное обеспечение автоматически обновляет Connections , Inputs , и Outputs свойства fistree объект. Для примера смотрите «Обновление Нечеткие Системы Вывода в Древовидном» примере FIS на fistree страница с описанием.

Настройте нечеткое дерево

Если вы сконфигурировали внутренние связи в своем нечетком дереве, следующий шаг должен настроить параметры дерева. Для примера смотрите Мелодию Дерево FIS для Предсказания Расхода бензина.

Ссылки

[1] Siddique, Nazmul и Hojjat Adeli. Вычислительный Интеллект: Совместные действия Нечеткой логики, Нейронных сетей и Эволюционного Вычисления . Оксфорд, Великобритания: John Wiley & Sons Ltd, 2013. https://doi.org/10.1002/9781118534823.

Смотрите также

Похожие темы

Источник

Презентация, доклад Нечеткий вывод и деревья решений

Вы можете изучить и скачать доклад-презентацию на тему Нечеткий вывод и деревья решений. Презентация на заданную тему содержит 45 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Источник