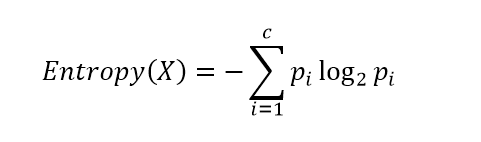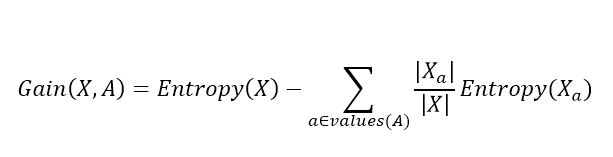Использование деревьев решений в задачах прогнозной аналитики
В последние десятилетия одними из самых популярных методов решения задач прогнозной аналитики являются методы построения деревьев решений. Эти методы универсальны, используют эффективную процедуру вычислений, позволяют найти достаточно качественное решение задачи. Именно об этих методах я расскажу в данной статье.
Дерево решений
Дерево решений – структура данных, в процессе обхода которой в каждом узле в зависимости от проверяемого условия принимается определенное решение – перемещение по той или иной ветке дерева от корня к «листьевым» (конечным) вершинам. В «листьевой» вершине дерева содержится искомое значение интересующего атрибута. Деревья решений могут оценивать значения категориальных атрибутов (конечное число дискретных значений), а также количественных. В первом случае говорят о задаче классификации – отнесении объекта к одному из «классов», определяемых атрибутом (например, Да/Нет, Хорошо/Удовлетворительно/Плохо и т.д.). Во втором случае говорят о задаче регрессии, то есть об оценке количественной величины.
Мы рассмотрим алгоритм, позволяющий построить такое дерево решений для оценивания и предсказания значений интересующего нас категориального атрибута анализируемого набора данных на основе значений других атрибутов (задача классификации).
Вообще способов построить дерево может быть бесконечно много – атрибуты можно рассматривать в разном порядке, проверять в узлах дерева различные условия, останавливать процесс, используя разные критерии. Но нас интересуют только деревья, которые наиболее точно оценивают значение атрибута, с минимальной ошибкой, а также позволяют выявлять зависимость между атрибутами и успешно выполнять прогнозирование значений атрибутов на новых данных. К сожалению, не существует хороших алгоритмов, позволяющих гарантированно найти такое «оптимальное» дерево (за приемлемое время). Однако существуют достаточно хорошие алгоритмы, которые пытаются построить «почти оптимальное» дерево, выполняя на каждой итерации определенный «локальный» критерий оптимальности в надежде, что получившееся дерево тоже в целом будет «оптимальным». Такие алгоритмы называются «жадными». Именно такой алгоритм мы и рассмотрим.
Алгоритм построения дерева решений
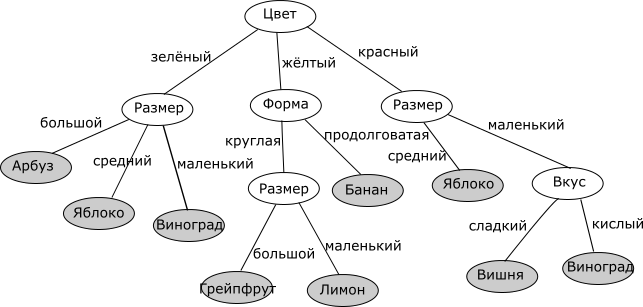
Принцип построения дерева следующий. Дерево строится «сверху вниз» от корня. Начинается процесс с определения, какой атрибут следует выбрать для проверки в корне дерева. Для этого каждый атрибут исследуется на предмет, как хорошо он в одиночку классифицирует набор данных (разделяет на классы по целевому атрибуту). Когда атрибут выбран, для каждого его значения создается ветка дерева, набор данных разделяется в соответствии со значением к каждой ветке, процесс повторяется рекурсивно для каждой ветки. Также следует проверять критерий остановки.
Главный вопрос – как выбирать атрибуты. В соответствии с идеей подхода, когда в концевых узлах дерева (листьях) будет искомый нами класс целевого атрибута, необходимо, чтобы при разбиении набора данных в каждом узле получавшиеся наборы данных были все более однородны в плане значений классов (например, большинство объектов в наборе принадлежало бы к классу Арбуз). И необходимо определить количественный критерий, чтобы оценить однородность разбиения.
Энтропия
Рассмотрим набор вероятностей pi, описывающий вероятность соответствия строки данных в нашем наборе (обозначим его X) классу i. Вычислим следующую величину:
Данная функция представляет собой так называемую энтропию. Энтропия возникла в теории информации и описывает количество информации (в битах), которое необходимо, чтобы закодировать сообщение о принадлежности случайно выбранного объекта (строки) из нашего набора X к одному из классов и передать его получателю. Если класс только один, получателю ничего не нужно передавать, энтропия равна 0 (принимается, что 0log20 = 0). Если все классы равновероятны, то потребуется log2c бит (c – общее количество классов) – максимум функции энтропии.
Далее, для выбора атрибута, для каждого атрибута A вычисляется так называемый прирост информации:
Где values(A) – все принимаемые значения атрибута A, Xa – подмножество набора данных, где A = a, |X| – количество элементов во множестве. Данная величина описывает ожидаемое уменьшение энтропии после разбиения набора данных по выбранному атрибуту. Второе слагаемое – это сумма энтропий для каждого подмножества, взятая со своим весом. Общая разница описывает, как уменьшится энтропия, сколько мы сэкономим бит для кодирования класса случайного объекта из набора X, если мы знаем значения атрибута A и разобьем набор данных на подмножества по данному атрибуту.
Алгоритм выбирает атрибут, соответствующий максимальному значению прироста информации.
Когда атрибут выбран, исходный набор разбивается на подмножества в соответствии с его значениями, исходный атрибут исключается из анализа, процесс повторяется рекурсивно.
Процесс останавливается, когда созданные подмножества стали достаточно однородны (преобладает один класс), а именно когда max(Gain(X,A)) становится меньше некоторого заданного параметра Θ (величина, близкая к 0). Как альтернативный вариант, можно контролировать само множество X, и когда оно стало достаточно мало или стало полностью однородным (только один класс), останавливать процесс.
Жадный алгоритм построения дерева решений
Более структурно алгоритм можно представить следующим образом:
1. Если max(Gain(X,A))
Источник
2.8 Метод построения деревьев решений проекта
В сложных ситуациях, когда трудно вычислить результат проекта с учетом возможных рисков, используют метод построения дерева решений проекта. Он позволяет оценить риски решений, имеющие обозримое количество вариантов развития. Этот метод удобно применять в случае небольшого числа риск-факторов и возможных сценариев развития проекта. Преимущество данного метода состоит в его наглядности [15].
Метод дерева решений состоит из нескольких этапов.
На первом этапе формулируется задача. Отбрасываются не относящиеся к проблеме факторы, а оставшиеся подразделяются на существенные и несущественные. Далее определяются возможности сбора информации для экспериментирования и реальных действий; составляются перечень событий, которые с определенной вероятностью могут произойти: устанавливаются временной порядок расположения событий, в исходах которых содержится полезная и доступная информация, и тех последовательных действий, которые можно предпринять.
На втором этапе строится дерево решений. Оно состоит из двух основных частей: «решений» и «вероятностных событий». Они представлены квадратами Эти решения и вероятностные события связаны.
Суть третьего этапа состоит в оценке вероятностей состояний среды, т.е. сопоставлении шансов возникновения каждого конкретного события.
Установление выигрышей (или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации альтернатив (действий) состояний среды составляют четвертый этап.
На пятом этапе решается задача.
Дерево решений — это графический инструмент для анализа проектных ситуаций, находящихся под воздействием риска. Дерево решений описывает рассматриваемую ситуацию с учетом каждой из имеющихся возможностей выбора и возможного сценария.
Дерево решений имеет пять основных элементов:
- Точки принятия решений — это моменты времени, когда происходит выбор альтернатив.
- Точка случайного события или точка возникновения последствий — это момент времени, когда с тем или иным результатом наступает случайное событие.
- Ветви — это линии, соединяющие точки принятия решений с точками случайного события. Ветви, исходящие из точки принятия решений, показывают возможные решения, а линии, исходящие из узлов случайных событий, представляют возможные результаты случайного события [15].
- Вероятности — это числовые значения, расположенные на ветвях дерева и обозначающие вероятность наступления этих событий. Сумма вероятностей в каждой точке принятия решений равна 1.
- Ожидаемое значение (последствия) — это расположенное в конце ветви количественное выражение каждой альтернативы [15].
Модель создается слева направо. Построение начинается с отображения точки принятия решения, имеющей вид квадрата. Из этой точки строят количество ветвей, равное числу проектных альтернативных решений. В конце каждой ветви находится узел в виде круга, обозначающий возникновение допустимого случайного события, из которого выходят возможные результаты вероятностного события в виде ветвей. Ветви дерева берут свое начало в точке принятия решений и разрастаются до получения конечных результатов. Путь вдоль ветвей дерева состоит из последовательности отдельных решений и случайных событий [15].
В результате построения дерева решений определяется вероятность возникновения каждого варианта развития проекта и результат по каждому варианту.
На рисунке 2.11 изображен пример дерева решений для проектной ситуации, находящейся под воздействием риска [15].
Рисунок 2.11 — Пример дерева решений
В данном примере основные результаты дерева решения вычисляются следующим образом (расчеты выполняются справа налево):
где — ожидаемое значение варианта 1 для случайного узла А;
— возможные результаты случайного события А;
— вероятность наступления возможных результатов случайного события А.
где — ожидаемое значение варианта 2 для случайного узла В;
— возможные результаты случайного события В;
— вероятность наступления возможных результатов случайного события В.
где — ожидаемое значение варианта 3 для случайного узла С;
— возможные результаты случайного события С;
— вероятность наступления возможных результатов случайного события С.
Результат дерева решения — выбор такого варианта развития проекта, который наилучшим образом удовлетворяет заданным условиям (например, по наименьшей стоимости или наименьшим срокам проекта внедрения).
Ограничением практического использования метода построения дерева решений проекта является исходная предпосылка о том, что проект должен иметь обозримое или разумное число вариантов развития. Метод особенно полезен в ситуациях, когда решения, принимаемые в каждый момент времени, сильно зависят от решений, принятых ранее, и в свою очередь определяют сценарии дальнейшего развития событий [17].
Достоинства метода построения деревьев решений:
- простота и наглядность реализации;
- комплексная оценка всех вероятных исходов проекта;
- экспертные оценки более обоснованы, так как эксперты оценивают вероятность отдельных этапов проекта, а не весь проект в целом;
- возможность учета отклонений закона распределения издержек, цен и объемов продаж от нормального.
Недостатки метода построения деревьев решений:
- наличие большого числа вероятных исходов решений, что приводит к снижению вероятности каждого из них.
Метод построения деревьев решений применим при оценке рисков проектов внедрения информационных систем различных классов, т.к. при ограниченном объеме информации данный метод позволяет комплексно оценить вероятность всех исходов проекта, сохраняя простоту и наглядность реализации. Он позволяет строить различные варианты осуществления проекта поэтапно. При применении метода деревьев решений эксперты могут оценивать вероятность отдельных этапов проекта, а не весь проект целиком, что делает экспертные оценки более обоснованными.
Источник