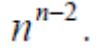какая-то теория / деревья
Деревья Рассмотрим особый вид графов, называемый «деревом». Впервые ввел понятие деревьев физик Г. Кирхгофф в 1847 году. Будучи студентом Кёнигсбергского университета, он сформулировал законы, управляющие течением тока в электрических сетях. Сети проводов могут быть рассмотрены как графы. Уравнения, которые вытекают из законов Кирхгоффа, не являются независимыми, и Кирхгофф использовал деревья для получения независимого подмножества уравнений. Независимо от Кирхгоффа А. Кэли, перечисляя изомеры насыщенных углеводородов, еще раз ввел понятие деревьев и первым исследовал их свойства. Как чисто математический объект деревья были введены и исследованы К. Жорданом.
Неориентированные деревья Неориентированным деревом называется связный неориентированный граф, не содержащий циклов. Можно сказать, что дерево является минимальным связным графом в том смысле, что при удалении хотя бы одного ребра он теряет связность. Несвязный неориентированный граф без циклов, связные компоненты которого есть деревья, называется лесом . Любая часть леса или дерева также не имеет циклов, то есть является лесом или деревом.
Свойства деревьев Теорема . Пусть граф G = (V, E) имеет n вершин и m ребер. Тогда эквивалентными являются такие утверждения: 1) G является деревом; 2) G является ациклическим графом и m = n −1; 3) G является связным графом и m = n −1; 4) любые две вершины графа G соединяет единственная простая цепь; 5) G является ациклическим графом, но добавление любого нового ребра способствует возникновению ровно одного цикла.
Деревья Следствие . В любом дереве с числом вершин n ≥ 2 имеется не менее двух концевых вершин. Следствие . Пусть G − лес с n вершинами и k компонентами, тогда G имеет n − k ребер. Теорема (теорема Кэли). Число различных деревьев, которые можно построить на n вершинах, равно
Остовное дерево Остовным деревом или остовом неориентированного графа G называется остовной подграф, содержащий все вершины графа G и являющийся деревом. Остовным лесом неориентированного графа G называется остовной подграф, являющийся лесом. В каждом графе существует остовное дерево. Его можно получить при помощи алгоритма поиска в ширину.
Остовное дерево Построение последовательности деревьев при нахождении остовного дерева алгоритмом поиска в ширину равносильно удалению лишних ребер в каждом цикле исходного графа. Число ребер, которые необходимо удалить в графе G для получения остовного дерева, называется цикломатическим числом графа G и обозначается v(G) .
Источник
Построение всех остовных деревьев графа
В ряде случаев возникает необходимость в построении полного списка остовных деревьев графа G. Например, в том случае, когда надо отобрать «наилучшее» дерево, а критерий, позволяющий осуществить такой отбор, является очень сложным (или даже частично субъективным), так что непосредственное решение задачи оптимизации (не использующее перечисление всех остовных деревьев) оказывается невыполнимым.
Число различных остовов полного связного неориентированного помеченного графа с n вершинами равно 

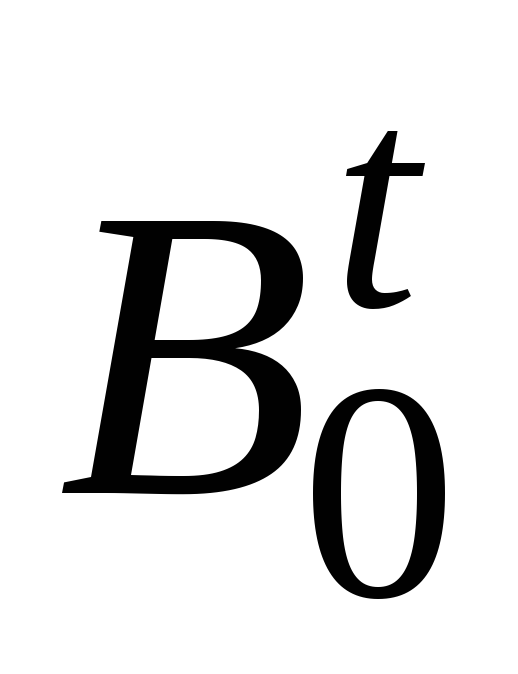
Элементарные преобразования деревьев
Рассмотрим два (ориентированных или неориентированных) остовных дерева 
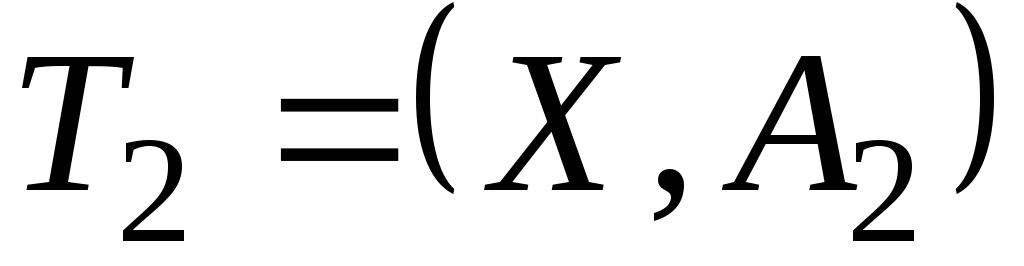










,
где 
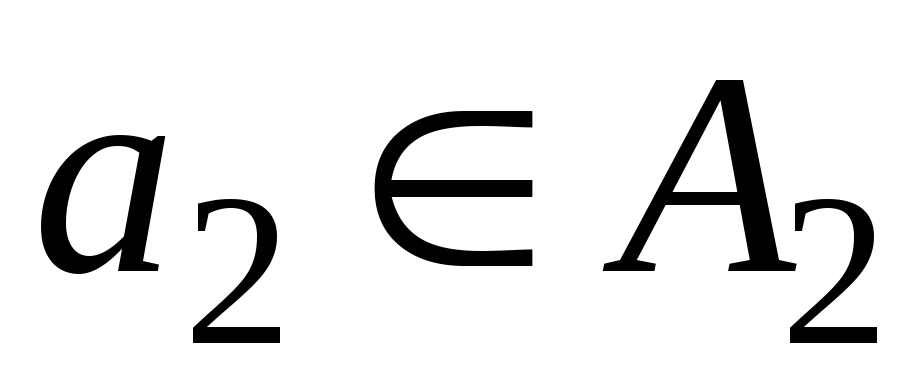
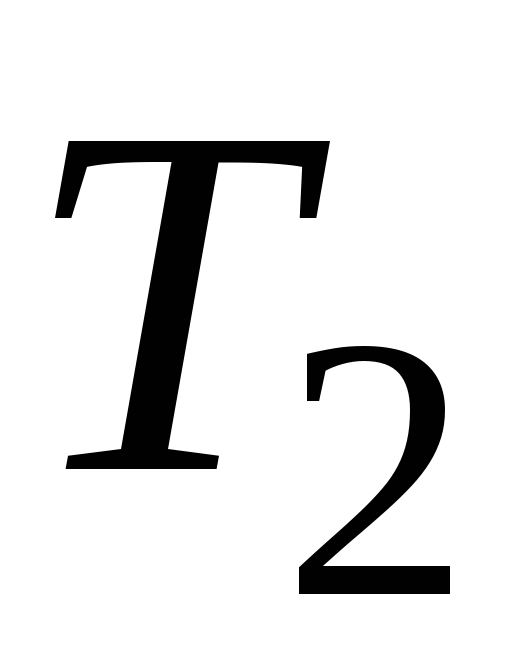


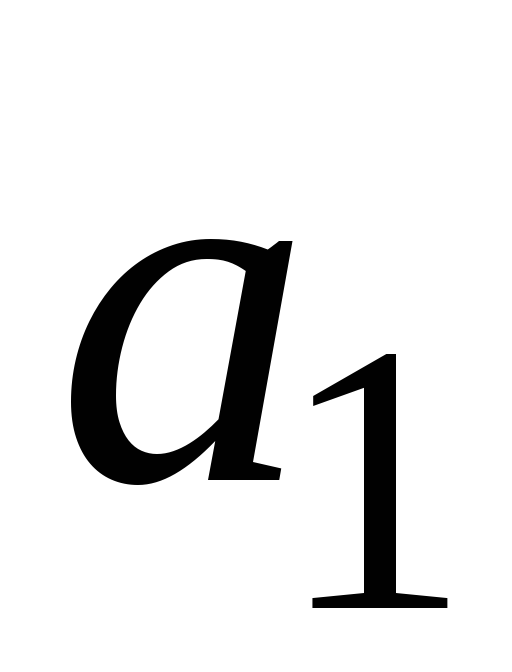

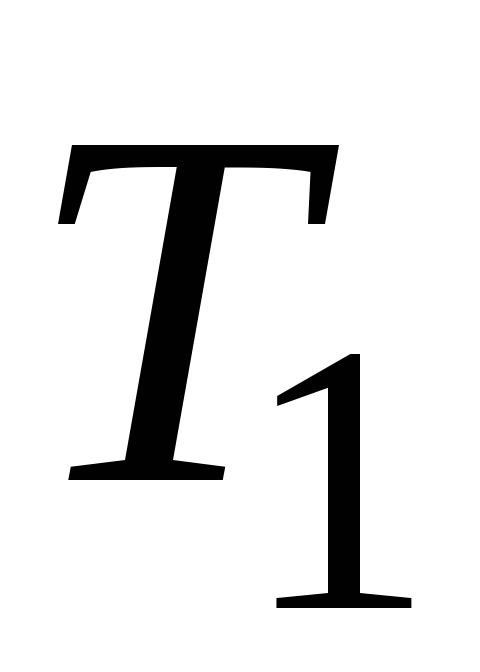

Рис.3. Остовы T0 и T4.
Существует теорема, согласно которой дерево Tk может быть получено из дерева T0 с помощью серий из k элементарных преобразований при =k.
Процедура порождения всех деревьев неориентированного графа
Первый шаг состоит в приписывании номеров ребрам графа G (ребра нумеруются от 1 до m, где m — число ребер в графе G). На каждом этапе (т. е. при каждом ветвлении в дереве решений) выбирается ребро, которое вместе с остальными, выбранными уже на предыдущих этапах, будет образовывать часть конструируемого дерева. Таким образом, прежде чем отобрать такое ребро, выясняют, действительно ли добавление его к частично сформированному дереву (которое на этом шаге является набором поддеревьев) не приводит к появлению цикла. Если цикл появляется, то данное ребро отбрасывается и проверке подвергается следующее ребро, с большим номером. Если цикла нет, то ребро добавляется к другим, уже отобранным, и процесс продолжается до тех пор, пока не будет построено остовное дерево. Ребра перебираются в порядке возрастания их номеров; это приводит к исчерпывающему и без повторений решению задачи.
Для облегчения манипуляций с поддеревьями в каждом поддереве выделяют произвольным образом корень (некоторую вершину поддерева) и затем рассматриваю поддерево уже как древовидность. Для организации проверки на возможность образования (при добавлении ребра) каждую вершину xj помечают парой (rj, pj). Первая пометка rj указывает «корень» поддерева, содержащего вершину xj. Первоначально rj = xj для всех вершин xj. На некотором шаге два поддерева T1, и T2 сращиваются посредством добавления ребра al=(xa, xb) с вершиной xa из T1 и вершиной xb из T2. Если на этом шаге r1 — «корневая» пометка вершин в T1, а r2 — «корневая» пометка вершин в T2 и для примера r1 < r2, то все вершины в T2, должны «сменить» свои корневые пометки на r1, и два поддерева T1 и T2 «сольются» в единственное новое дерево T1.
Вторая пометка pj, приписанная вершине xj, указывает вершину, предшествующую вершине xj, т.е. если =(xk, xj) — дуга рассматриваемого поддерева, то pj = xk. Для корневой вершины дерева такая пометка полагается равной нулю.
А. Замена корня дерева
Если корнем дерева T является вершина r и нужно в качестве корня выбрать новую вершину xs, то такую «замену» r на xs можно осуществить простым обращением ориентации дуг, принадлежащих цепи, идущей от r к xs, не меняя при этом ориентацию других дуг. Соответствующие изменения пометок будут таковы.
Изменение пометок «предшествования»
- Пусть xj = xs и z = pj.
- Положить xi = z, a z = pi.
- Шаг обновления: pi = xj.
- Если xi = r, то перейти к шагу 5. в противном случае положить xj = xi и перейти к шагу 2.
- Положить ps = 0, стоп.
Изменение корневых пометок У всех вершин, имеющих корневую пометку r, заменить ее на пометку xs.Б.Сращивание двух поддеревьев Если осуществлено сращивание двух поддеревьев T1 и T2 (путем добавления ребра (xa, xb)), то в пометки необходимо внести следующие изменения: (1) У вершин с корневой пометкой r2 заменить эту пометку на r1. (2) Заменить в дереве T2 корень r2 на xb (пункт А), после чего изменить пометку «предшествования» у вершины xb с pb = 0 на pb = xa. B.Расщепление дерева на две части Поскольку метод порождения деревьев, рассматриваемый ниже, является поиском, использующим дерево решений, то возникает необходимость удаления некоторых ребер (на шагах возвращения), чтобы испытать затем другие ребра. В такой ситуации удаление ребра приводит к расщеплению некоторого дерева на две части, например на T1 и T2, и в пометки одного из этих поддеревьев должны быть внесены изменения. Пусть удаляется ребро (xa, xb), где xaÎT1 и xbÎT2. Тогда при pb = xa (т. е. если ребро (xa, xb) в первоначальном дереве ориентировано от xa к xb) пометки в дереве T1, можно оставить прежними, а пометки в дереве T2 должны быть изменены. Если же pa = xb (т. е. ребро (xa, xb) ориентировано от xb к xa), то можно не менять пометки в дереве T2, но нужно изменить пометки в T1. Предполагая, что пометки меняются в дереве T2, покажем, как надо «восстанавливать» корень в этом дереве.
- Положить S = xb> и pb = 0 (xb будет корнем дерева T2).
- Найти все вершины xj с pjÎS и изменить их корневые пометки на rj = xb. Если таких вершин нет, остановиться.
- Шаг обновления: S = S È xj|pjÎS>; вернуться к шагу 2.
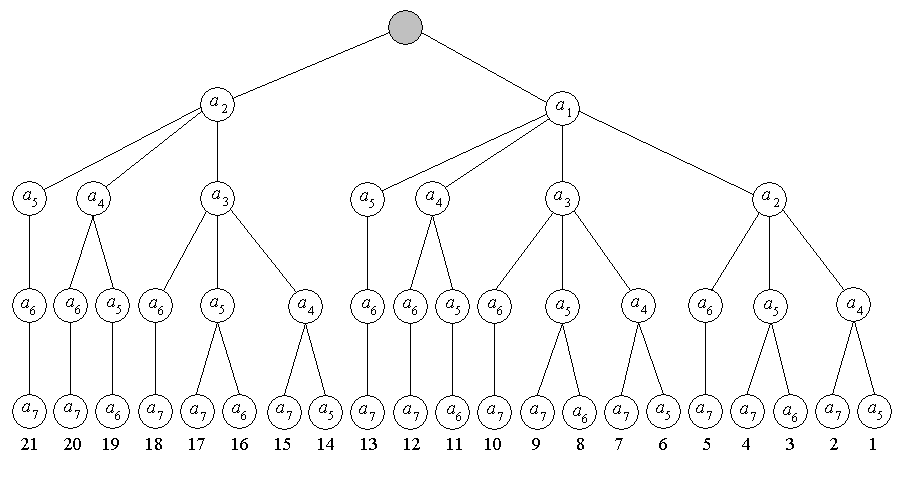
Следует отметить, что ни у одной вершины, кроме нового корня xb, пометки предшествования менять не нужно. Заметим также, что число описанных выше шагов 2 и 3, которое необходимо для восстановления корня, равно длине самой длинной цепи в T2 исходящей из вершины xb.Описание алгоритма. Возьмем произвольную вершину x * графа G. Пусть ее степень равна d * . Перенумеруем ребра, инцидентные этой вершине: a1, a2, …, ad*. Затем перенумеруем остальные ребра графа G:ad*+1, ad*+2, …, am. При порождении деревьев ребра будут перебираться в соответствии с введенной нумерацией. Шаг 1. Приписать вершинам пометки: (ri, pi), где ri=xi и pi=0, «xiÎX. Положить k=1. Шаг 2. Выбрать для исследования некоторое ребро. Например, ak=(xi, xj). Если k≤m, где m — число ребер графа, то перейти к 2 (1). При k=m+1, т. е. если «неисследованных» ребер нет, перейти к шагу 5. (1) Если ri=rj, то это означает, что вершины xi и xj принадлежат одному и тому же поддереву и добавление ребра ak приведет к появлению цикла. Отбросить ребро ak, т. е. положить k=k-1 и вернуться к шагу 2. (2) Если ri≠rj то ребро ak можно добавить к ребрам построенных поддеревьев. Перейти к шагу 3. Шаг 3. Срастить два поддерева, у которых вершины имеют корневые пометки ri и rj, применив для этого метод, описанный выше в пункте Б. Шаг 4. Отобрав n-1 ребер, мы получаем некоторое дерево. Заполнить это дерево и перейти к шагу 5. Если отобрано меньше, чем n-1 ребер, то положить k=k+1 и вернуться к шагу 2. Шаг 5. (Возвращение.) Удалить ребро, добавленное последним. Предположим, что таким ребром является al. Если al — единственное оставшееся для добавления ребро, l=d * то остановиться. Все остовные деревья, таким образом построены, т. к. при любом дальнейшем ветвлении дерева решений вершина x * останется изолированной. В противном случае надо обновить пометки, действуя так, как указано в пункте B, положить k=l-1 и возвратиться к шагу 2. Пример Построим все остовные деревья графа, изображенного на рис.4. Выберем в качестве x * вершину x1. 




Источник