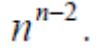какая-то теория / деревья
Деревья Рассмотрим особый вид графов, называемый «деревом». Впервые ввел понятие деревьев физик Г. Кирхгофф в 1847 году. Будучи студентом Кёнигсбергского университета, он сформулировал законы, управляющие течением тока в электрических сетях. Сети проводов могут быть рассмотрены как графы. Уравнения, которые вытекают из законов Кирхгоффа, не являются независимыми, и Кирхгофф использовал деревья для получения независимого подмножества уравнений. Независимо от Кирхгоффа А. Кэли, перечисляя изомеры насыщенных углеводородов, еще раз ввел понятие деревьев и первым исследовал их свойства. Как чисто математический объект деревья были введены и исследованы К. Жорданом.
Неориентированные деревья Неориентированным деревом называется связный неориентированный граф, не содержащий циклов. Можно сказать, что дерево является минимальным связным графом в том смысле, что при удалении хотя бы одного ребра он теряет связность. Несвязный неориентированный граф без циклов, связные компоненты которого есть деревья, называется лесом . Любая часть леса или дерева также не имеет циклов, то есть является лесом или деревом.
Свойства деревьев Теорема . Пусть граф G = (V, E) имеет n вершин и m ребер. Тогда эквивалентными являются такие утверждения: 1) G является деревом; 2) G является ациклическим графом и m = n −1; 3) G является связным графом и m = n −1; 4) любые две вершины графа G соединяет единственная простая цепь; 5) G является ациклическим графом, но добавление любого нового ребра способствует возникновению ровно одного цикла.
Деревья Следствие . В любом дереве с числом вершин n ≥ 2 имеется не менее двух концевых вершин. Следствие . Пусть G − лес с n вершинами и k компонентами, тогда G имеет n − k ребер. Теорема (теорема Кэли). Число различных деревьев, которые можно построить на n вершинах, равно
Остовное дерево Остовным деревом или остовом неориентированного графа G называется остовной подграф, содержащий все вершины графа G и являющийся деревом. Остовным лесом неориентированного графа G называется остовной подграф, являющийся лесом. В каждом графе существует остовное дерево. Его можно получить при помощи алгоритма поиска в ширину.
Остовное дерево Построение последовательности деревьев при нахождении остовного дерева алгоритмом поиска в ширину равносильно удалению лишних ребер в каждом цикле исходного графа. Число ребер, которые необходимо удалить в графе G для получения остовного дерева, называется цикломатическим числом графа G и обозначается v(G) .
Источник
§ 3.8. Деревья, лес
Определение 3.8.1. Неориентированным деревом (или просто деревом) называется связный граф без циклов. Дерево есть связный граф, содержащий n вершин и n – 1 ребер, дерево есть граф, любые две вершины которого можно соединить простой цепью.
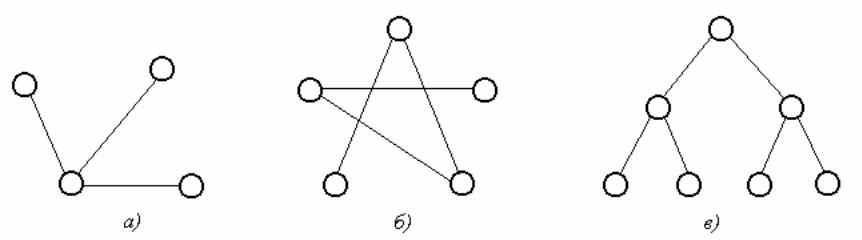
Пример. Графы, изображенные на рис 21, являются деревьями.
рис.21
Если граф несвязный и не имеет циклов, то каждая его связная компонента будет деревом. Такой граф называется лесом. Можно интерпретировать рис.21 как лес, состоящий из трех деревьев.
Определение 3.8.2. Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.
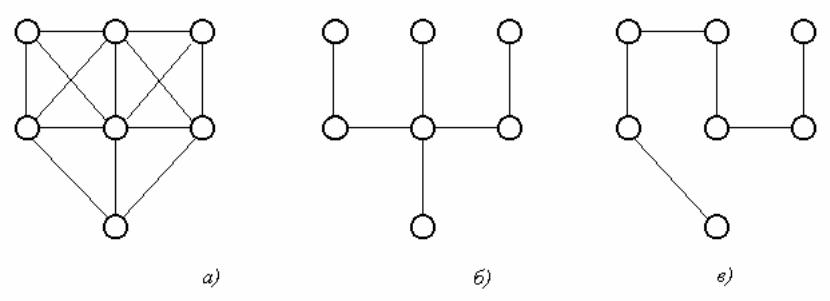
Пример. Для графа, изображенного на рис. 22 а), графы на рис. б и в являются остовными деревьями.
рис.22
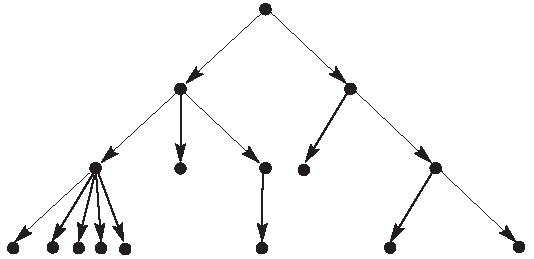
Определение 3.8.3. Ориентированным деревом называют граф, в котором в каждую вершину, кроме одной, называемой корнем дерева, заходит ровно одна дуга. В корень дерева ни одна дуга не заходит. Вершины, из которых не выходит ни одна дуга, называются листьями (рис.23).
рис.23
§ 3.9. Взвешенные графы
Определение 3.9.1. Взвешенный граф – это граф дугам, которого поставлены в соответствие веса, так что дуге (xi, xj) сопоставлено некоторое число c (xi, xj) = cij, называемое длиной (или весом, или стоимостью) дуги. Обычный (не взвешенный) граф можно интерпретировать как взвешенный, все ребра которого имеют одинаковый вес 1.
Определение 3.9.2. Длина пути во взвешенном графе — это сумма длин (весов) тех ребер, из которых состоит путь.
Определение 3.9.3. Расстояние между вершинами – это длина кратчайшего пути. Например, расстояние от вершины a до вершины d во взвешенном графе, изображенном на рис. 24, равно 6.
рис.24
Примеры взвешенных графов
§ 3.10. Эйлеровы и гамильтоновы графы
Определение 3.10.1. Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом.
Определение 3.10.2. Если граф имеет цепь (не обязательно простую), содержащую все вершины по одному разу, то такая цепь называется эйлеровой цепью, а граф называется полуэйлеровым графом.
Эти понятия возникли в статье Эйлера в 1735 г., в которой он решал задачу о Кенигсбергских мостах и впервые ввел понятие графа. На рис.25, а приведен план расположения семи мостов в Кенигсберге (ныне Калининграде). Задача состоит в том, чтобы пройти каждый мост по одному разу и вернуться в исходную точку С. Поскольку в конце обхода нужно вернуться в исходную часть города, и на каждом мосту нужно побывать по одному разу, этот маршрут является простым циклом, содержащим все ребра графа. В дальнейшем такие циклы и стали называть эйлеровыми, а графы, имеющие эйлеров цикл – эйлеровыми графами.
Эйлеров цикл можно считать следом пера, вычерчивающего этот граф, не отрываясь от бумаги. Таким образом, эйлеровы графы – это графы, которые можно изобразить одним росчерком пера, причем процесс такого изображения начинается и заканчивается в одной и той же точке.
Обнаружив, что в данном графе не существует циклических обходов, проходящих по всем ребрам по одному разу, Эйлер обратился к общей задаче: при каких условиях в графе можно найти такой цикл? Ответ на этот вопрос дает следующая теорема.
Теорема Эйлера. Чтобы в связанном неориентированном графе G существовал эйлеров цикл, необходимо и достаточно, чтобы число вершин нечетной степени было четным.
Определение 3.10.3. Гамильтоновой цепью графа называется его простая цепь, которая проходит через каждую вершину графа точно один раз.
Определение 3.10.4. Цикл графа, проходящий через каждую его вершину, называется гамильтоновым циклом.
Определение 3.10.5. Граф называется гамильтоновым, если он обладает гамильтоновым циклом.
Гамильтоновы графы применяются для моделирования многих практических задач, например, служат моделью при составлении расписания движения поездов. Основой всех таких задач служит классическая задача коммивояжера: коммивояжер должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, сведя при этом затраты на передвижения к минимуму.
Графическая модель задачи коммивояжера состоит из гамильтонова графа, вершины которого изображают города, а ребра — связывающие их дороги. Кроме того, каждое ребро оснащено весом, обозначающим транспортные затраты, необходимые для путешествия по соответствующей дороге, такие, как, например, расстояние между городами или время движения по дороге. Для решения задачи необходимо найти гамильтонов цикл минимального общего веса.
Теорема Кёнига. В полном конечном графе всегда существует гамильтонов путь.
Если в графе G(X) с n вершинами для любой пары вершин xi и xj справедливо неравенство
где m(хi), m(xj) – степени вершин хi и xj, то граф G(X) имеет гамильтонову цепь.
Несмотря на сходство в определении эйлерова и гамильтонового циклов, соответствующие теории для этих понятий имеют мало общего. Критерий существования для эйлеровых циклов был установлен просто, для гамильтоновых циклов никакого общего правила неизвестно. Более того, иногда даже для конкретных графов бывает трудно решить, можно ли найти такой цикл. В принципе, поскольку речь идет о конечном числе вершин, задачу можно решить перебором, однако эффективного алгоритма неизвестно.
Источник