Неориентированный граф построение дерева

3 Покрывающие деревья (остовы)

Цикломатическим числом неориентированного графа G называется величина γ(G) = т — п + k, где т — число ребер, п — число вершин, k — число связных компонент. Для дерева и леса γ (G) = 0, для других графов γ (G) > 0.

Остовом, или покрывающим деревом, связного графа G=(V, E) называется часть G, которая содержит все его вершины и является деревом. Хордой остова графа G называется ребро G, не принадлежащее остову.

Очевидно, что любой связный граф имеет хотя бы один остов, а любой несвязный граф остова не имеет.

В последующем алгоритме части исходного графа G, которые возникают в процессе построения покрывающего дерева, будем называть букетами.

Алгоритм построения покрывающего дерева для произвольного невзвешенного графа g

1. Выбрать любое ребро G, не являющееся петлей. Пометить его меткой α и объявить букетом это ребро вместе с его концевыми вершинами.

2. Выбрать любое непомеченное ребро G, не являющееся петлей:

а) если один из концов выбранного ребра принадлежит построенному ранее букету В, а другой конец свободен (не принадлежит ни одному букету), пометить выбранное ребро меткой α, включить его вместе со свободным концом в букет В и перейти к шагу 3;

б) если оба конца выбранного ребра свободны, поме­тить его меткой а, объявить это ребро вместе с его конце­выми вершинами новым букетом и перейти к шагу 3;

в) если концы выбранного ребра принадлежат разным построенным ранее букетам В и С, пометить выбранное ребро меткой α, включить его и букет С в букет В и перейти к шагу 3;

г) если оба конца выбранного ребра принадлежат одному букету, пометить его меткой β и перейти к шагу 3;

д) если непомеченных ребер нет, закончить алгоритм.

3. Если все вершины графа G вошли в один букет, закончить алгоритм. Если нет, перейти к шагу 2.

Алгоритм выделения минимального остовного дерева в неориентированном взвешенном графе g

1. Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему двумя вершинами оно образует подграф G₂ графа G. Положим i:=2.
2. Если i=n(G), то задача решена и G_i – искомое минимальное остовное дерево графа G. Иначе переходим к шагу 3).
3. Строим граф G_i+1. Для этого добавим к графу G_i новое ребро минимальной длины из оставшихся, которое инцидентно какой-либо вершине графа G_i и одновременно вершине, не содержащейся в G_i. Вместе с этим ребром включаем в G_i+1 и эту инцидентную ему вершину. Присваиваем i:=i+1 и переходим к шагу 2.

Лекция 12 Двудольные и планарные графы

1 Двудольные графы

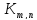
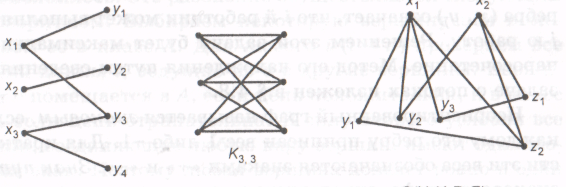
Двудольным графом G=(X, Y, Е) называется неориентированный граф, вершины которого можно разбить на два класса X и Y так, что концы каждого ребра принадлежат разным классам. Двудольный граф называется полным, если каждая вершина одной доли соединена с каждой вершиной другой доли, полный двудольный граф принято обозначать символом гдет = |Х|, n = . Введенные понятия допускают естественное обобще-ие. Неориентированный граф называется k-дольным, если его вершины можно разбить на k классов так, что концы каждого ребра принадлежат разным классам. Полный k-дольный граф — это k-дольный граф, в котором каждая вершина одной доли соединена с каждой вершиной всех остальных долей. Пример. На рисунке 24 представлены двудольный граф G=(X, Y, Е), полный двудольный граф К_3,3 и трехдольный граф G=(X, Y, Z, Е), где X = 1 x₂>, Y = 1 y₂, y₃>, Z = 1 z₂>. G=(X, Y, Е) G=(X, Y, Z, Е) Рисунок 24 – Двудольные графы Теорема. Граф является двудольным, если и только если длины всех его простых циклов четны. Паросочетанием в неориентированном графе называется множество попарно несмежных ребер. Задача о максимальном паросочетании заключается в нахождении паросочетания максимальной мощности. Для двудольного графа одной из наиболее известных интерпретаций задачи о максимальном паросочетании является задача о назначениях, которая заключается в следующем. Имеется т работников и п работ. Каждый работник способен выполнять несколько работ; каждую работу могут выполнять несколько работников. Требуется определить назначения по принципу «один работник — одна работа» так, чтобы загрузить максимальное число работников. Условия этой задачи представляются в виде двудольного графа, в котором вершины класса X соответствуют работникам, вершины класса Y- работам, а наличие ребра (x_i, y_j) означает, что i-й работник может выполнять j-ю работу. Решением этой задачи будет максимальное паросочетание, которое находится путем сведения к задаче о потоках.

Источник

8. Остовы и деревья

Понятие дерева широко используется во многих областях математики и информатики. Например, как инструмент при вычислениях, как удобный способ хранения данных, способ сортировки или поиска данных.

Достаточно развитое генеалогическое дерево образует дерево.

Типичное частичное организационное дерево для университета.

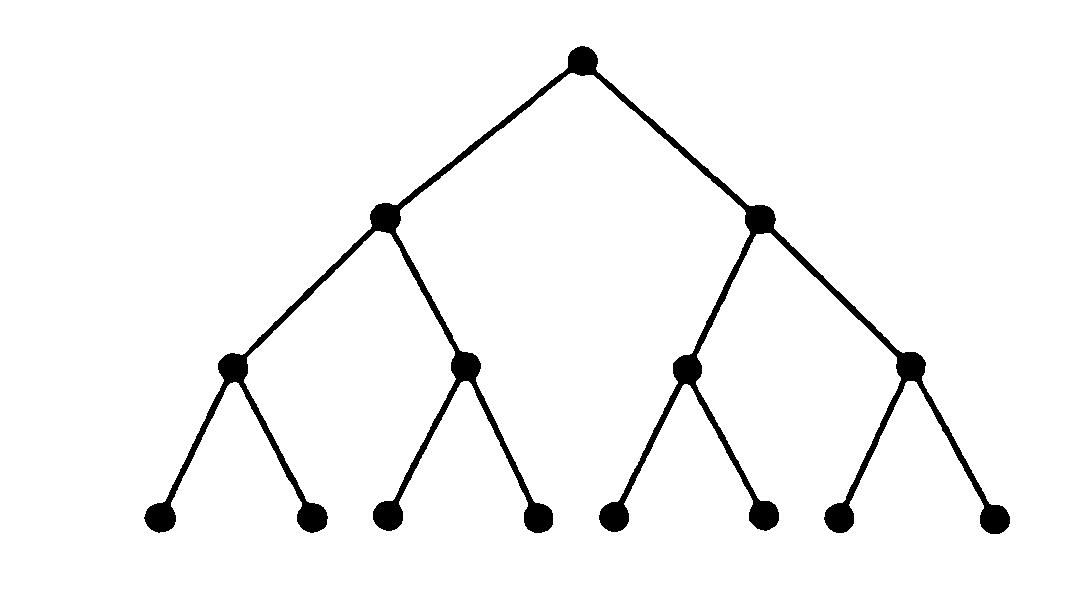
Если дерево имеет хотя бы одно ребро, оно имеет две вершины со степенью 1. Вершины со степенью 1 называются листьями. Другие вершины называются внутренними вершинами.

Предположим, что дерево представляет физический объект, подвижный в вершинах, и подвесим дерево за одну из его вершин:

Если подвесить за вершину V3 или V4

Вершина в верхней части называется корнем дерева, если корень определен, то дерево называется корневым. При необходимости корневое дерево Т можно заменить на ориентированное корневое дерево Т’, порожденное корневым деревом Т.

Если корень выбран, уровень вершины V определяется длиной единственного пути из корня в вершину V. Высотой дерева называется длина самого длинного пути от корня дерева до листа.

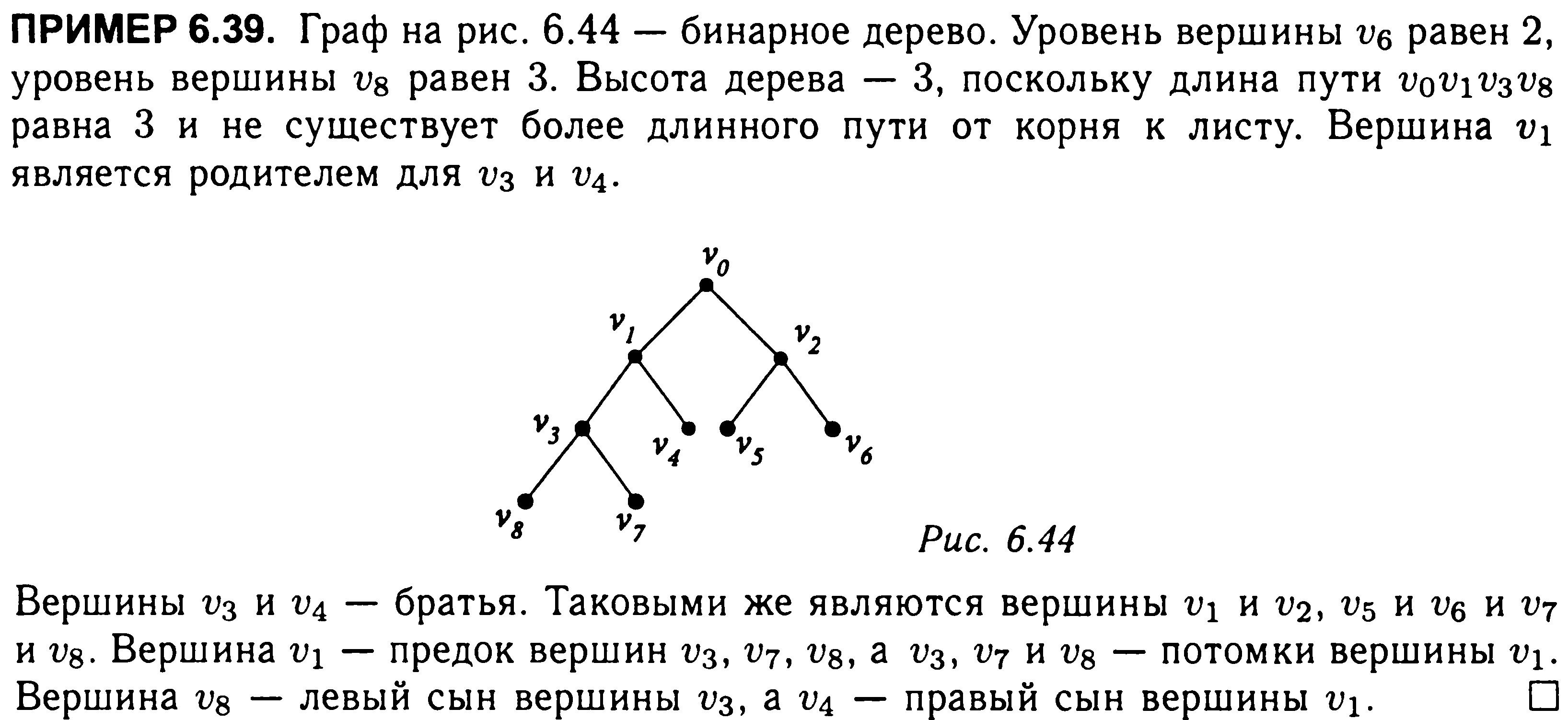
Если рассматривается корневое ориентированное дерево Т’, порожденное данным корневым деревом Т, тогда вершина u называется родителем вершины v; a v называется сыном вершины u, если существует ориентированное ребро из u в v.

Если u — родитель v и v1, тогда v и v1 называются братьями.

Если существует ориентированный путь из вершины u в вершину v, тогда u называется предком вершины v, a v называется потомком вершины u.

Если наибольшая из степеней выхода для вершин дерева равна m, тогда дерево называется m — арным деревом.

В частном случае, когда m = 2, дерево называется бинарным деревом.

В каждом бинарном дереве каждый сын родителя обозначается либо как левый сын, либо как правый сын (но не то и другое одновременно).

Связный граф G(V,E), не имеющий циклов, называется деревом.

ТЕОРЕМА (основные свойства деревьев):

Пусть граф G(V,E) имеет n вершин. Тогда следующие утверждения эквивалентны:

1. G является деревом;
2. G не содержит циклов и имеет n-1 рёбер;
3. G связен и имеет n-1 рёбер;
4. G связен, но удаление » ребра нарушает связность;
5. » две вершины графа G соединены ровно одним путём;
6. G не имеет циклов, но добавление » ребра порождает ровно один цикл.

Ориентированное дерево представляет собой ориентированный граф без циклов, в котором полустепень захода каждой вершины (за исключением одной, например v₁) не больше 1, а полустепень захода вершины v₁ (называемой также корнем) равна нулю. Вершину v ордерева называют потомком вершины u, если $ путь из u в v. В этом же случае вершину u называют предком вершины v. Вершину, не имеющую потомков, называют листом. 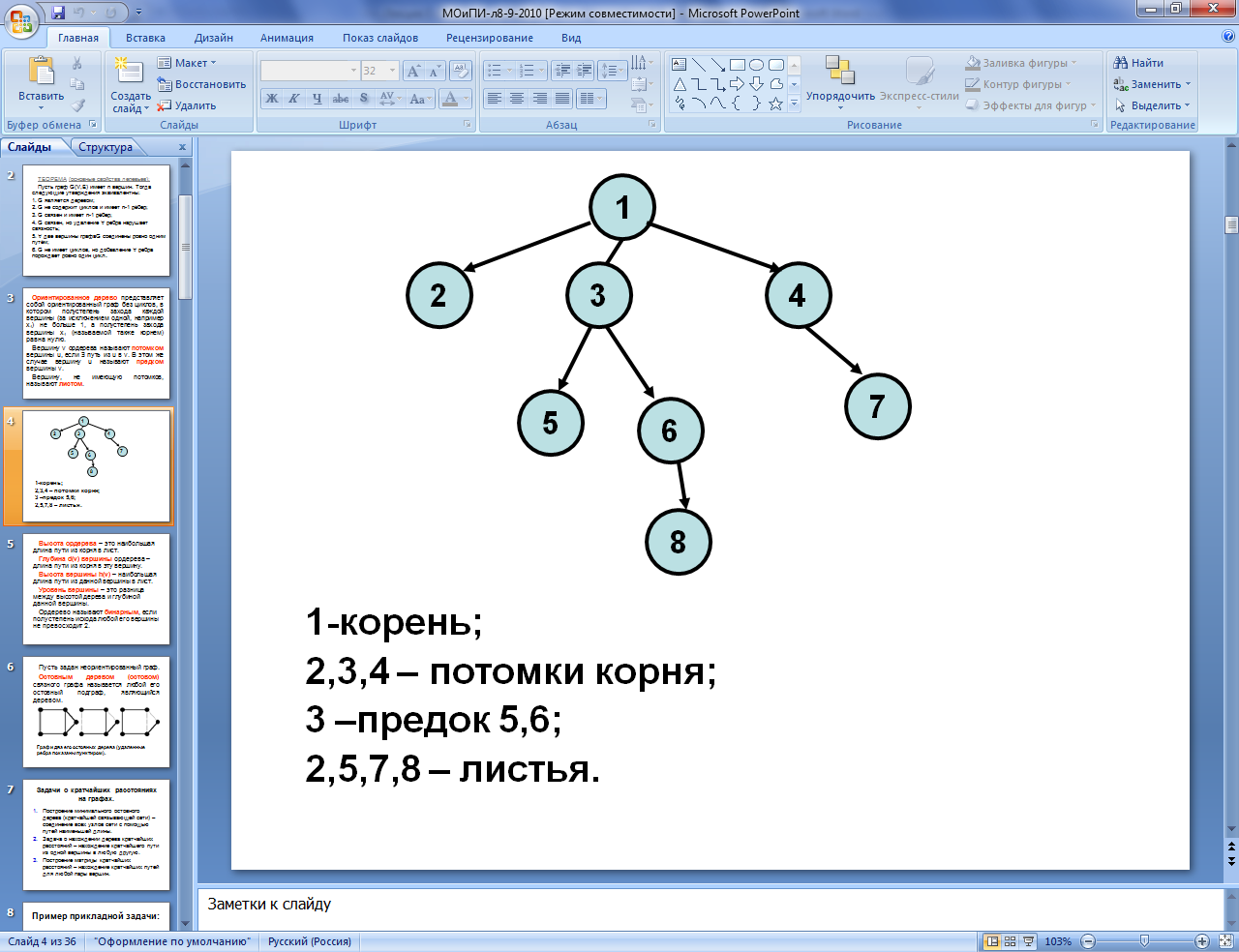Высота ордерева – это наибольшая длина пути из корня в лист. Уровень вершины ордерева – длина пути из корня в эту вершину. Ордерево называют бинарным, если полустепень исхода любой его вершины не превосходит 2. Пусть задан неориентированный граф. Остовным деревом (остовом) связного графа называется любой его остовный подграф, являющийся деревом. Граф и два его остовных дерева (удаленные ребра показаны пунктиром).Задачи о кратчайших расстояниях на графах.

1. Построение минимального остовного дерева (кратчайшей связывающей сети) – соединение всех узлов сети с помощью путей наименьшей длины.
2. Задача о нахождении дерева кратчайших расстояний – нахождение кратчайшего пути из одной вершины в любую другую.
3. Построение матрицы кратчайших расстояний – нахождение кратчайших путей для любой пары вершин.

Необходимо проложить линии коммуникаций (дороги, линии связи, электропередач и т.п.) между n заданными «точечными» объектами, при условии: во-первых, известны «расстояния» между каждой парой объектов (это может быть геометрическое расстояние или стоимость прокладки коммуникаций между ними), во-вторых, объекты могут быть связаны как непосредственно, так и с участием произвольного количества промежуточных объектов. При допущении, что разветвления возможны только в этих же n объектах, задача сводится к нахождению кратчайшего остовного дерева (SST — shortest spanning tree, или MST — minimal spanning tree) во взвешенном графе, вершины которого соответствуют заданным объектам, а веса ребер равны «расстояниям» между ними. Определение.Весостовного дерева взвешенного графа G равен сумме весов, приписанных ребрам остовного дерева. Будем обозначать (T). Минимальным остовным деревом (МОД) называется такое остовное дерево графа G, что вес T меньше или равен весу любого другого остовного дерева графа G. Вес минимального остовного дерева будем обозначать _min(T). Задача 1:найти кратчайшее остовное дерево (минимальный покрывающий остов) взвешенного графа. Пусть дан неориентированный связный граф со взвешенными ребрами. Вес ребра (x_i,x_j) обозначим c_ij. Из всех остовов графа необходимо найти один, у которого сумма весов на ребрах наименьшая. Стоимость остовного дерева вычисляется как сумма стоимостей всех рёбер, входящих в это дерево. Построение остова графа G, имеющего наименьший вес, имеет широкое применение при решении некоторого класса задач прикладного характера. Например: Пусть, например, G=(V, E, ) служит моделью железнодорожной сети, соединяющей пункты v₁, v₂, …, v_nV, а (v_i, v_j) – расстояние между пунктами v_i и v_j. Требуется проложить сеть телеграфных линий вдоль железнодорожной сети так, чтобы все пункты v₁, v₂, …, v_n были связаны между собой телеграфной сетью, протяженность которой была бы наименьшей. Рассмотрим два способа построения минимального остовного дерева взвешенного графа: алгоритм Крускала и алгоритм Прима. Алгоритм Крускала: 1) Выбрать в графе G ребро e минимального веса, не принадлежащее множеству E и такое, что его добавление в E не создает цикл в дереве T. 2) Добавить это ребро во множество ребер E. 3) Продолжить, пока имеются ребра, обладающие указанными свойствами. Пример. Для данного взвешенного графа найти минимальное корневое остовное дерево, используя алгоритм Крускала. Определить высоту построенного дерева. Алгоритм Крускала. Выбираем ребро с минимальным весом. Это ребро, (, ) с весом, равным 4. Пусть вершина будет корнем дерева. Далее выбираем ребра, инцидентные вершинам , и имеющие минимальный вес. Это ребро (, ) с весом 5. Затем к вершине присоединяем ребро (,) с весом 7. Далее, добавляем ребро (, ) с весом 7 и ребро (,) с весом 6. Минимальный вес построенного дерева равен: _min(T)=4+5+7+7+6=29.

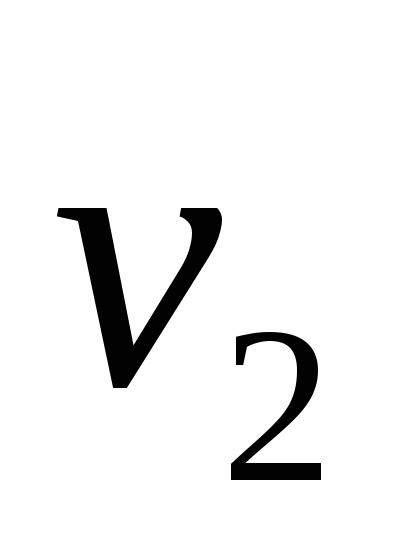
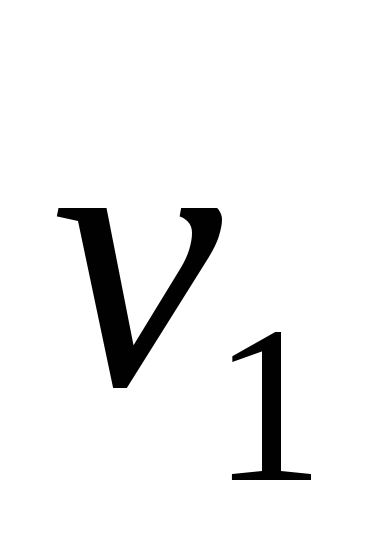
Источник