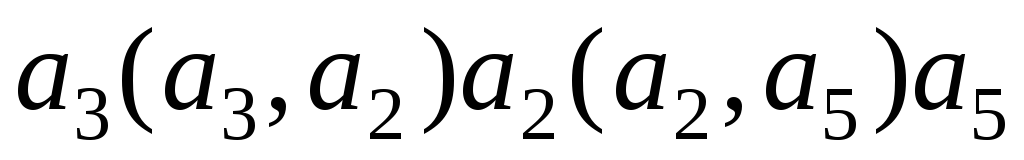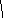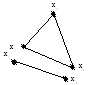Несвязный граф компонентами связности которого являются деревья называется

Связность в графах

Рассмотрим вопрос о связности в графах. Пусть G(X) – неори­ентированный граф. Две вершины х_i и x_j называются связными, если существует цепь S с концами х_i и x_j. Если S проходит через некото­рую вершину x_k более одного раза, то можно удалить цикл в верши­не x_k из цепи S. Отсюда следует, что вершины, связанные цепью, связаны элементарной цепью.

Неориентированный граф называется связным, если любая па­ра его вершин связана. Отношение связности для вершин графа есть отношение эквивалентности
(x_i ~ x_j, х_j ~ х_k Û x_i ~ х_k).

Компонентой связ­ности неориентирован­ного графа G(X) называ­ется подграф Н_А(А) графа G(X) с множеством вер­шин А Ì X и множеством ребер в G(X), инцидент­ных только вершинам из А, причем ни одна вершина x_i Î А не смежна с вершинами из множества Х \ А (рис. 3.12).

Рис. 3.12. Граф с двумя компонентами связности

Ориентированный граф называется сильно связным, если для любой пары вершин найдется путь, соединяющий их.

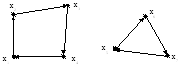
Компонентой сильной связности ориентированного графа G(X) называется подграф Н_А(А) графа G(Х) (подчиняющийся опре­делению сильно связного графа) с множеством вершин А Ì Х и мно­жеством дуг, имеющих начало и конец в А, причем ни одна из вер­шин х_i Î А и х_j Î X \ А не смежны между собой (рис. 3.13).

Рис. 3.13. Ориентированный граф с двумя компонентами сильной связности

Очевидно, что ориентированный граф G(X) сильно связан то­гда и только тогда, когда он имеет одну компоненту связности.

На практике широко используются такие виды графов, как де­ревья и прадеревья.

Деревом называется конечный связный неориентированный граф, состоящий, по крайней мере, из двух вершин и не содержащий циклов. Такой граф не имеет петель и кратных ребер (рис. 3.14).

Ветвями дерева называются ребра графа, вхо­дящие в дерево. Хордами дерева называются ребра, входящие в граф, дополнительный к данному дереву. Лагранжевым дере­вом называется дерево, все ветви которого имеют общую вершину.

Лесом называется несвязный граф, каждая компонента связно­сти которого является деревом.

Прадеревом называется ориентированный граф G(X) с корнем х₀ Î X, если в каждую вершину х_i ¹ х₀ (х_i Î X) заходит ровно одна дуга, а в корень х₀ не заходит ни одна дуга. Прадерево не содержит контуров (рис.3.15).

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

Пути. Циклы. Цепи в графах

Пусть G = (V, E) некоторый граф. Путем (маршрутом) в графе G, соединяющим вершины v₁ и v_n, называется любая чередующаяся последовательность вершин и ребер вида v₀,e ₀,v₁,e₁,v₂,e ₂…v_n-1,e _n-1,v_n, в которой каждое ребро e_i инцидентно вершинам v_i и v_i+1.

Путь называется замкнутым, если его начальная и конечная вершины совпадают.

Путь называется цепью, если все его ребра различны.

Цепь называется простой, если все ее вершины различны.

Замкнутая цепь называется циклом.

Цикл называется простым, если его вершины не повторяются.

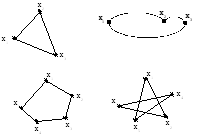
Вот схематическое изображение простого цикла:

А вот схематическое изображение цикла, не являющегося простым:

Для пути v₀, e ₀ ,v₁, e₁ , ….v_n число ребер n называется длиной пути.

Две вершины графа могут быть связаны некоторым путем: их называют связанными. Например, в графе

a₁

a₂ a₃ . a₄

вершины a₃ и a₅ связаны (путем ), а вершины a₄ и a₁ нет.

Простой граф – это граф, не содержащий петель и кратных ребер.

Граф называется связным, если для любой пары его вершин существует соединяющая их простая цепь. Т.о. граф связен, если из любой его вершины можно прийти к любой другой. Таким образом, выше приведен пример графа несвязного. Связной компонентой графа называется такой его подграф, который является сам по себе графом связным и при этом совпадающим с любым другим содержащим его связным подграфом. Таким образом, связный граф обладает единственной связной компонентой — это он сам. А вот пример графа с тремя связными компонентами (имена вершин не имеют значения):

Компонентой связности графа называется максимальный (по числу вершин и ребер) связный подграф этого граф.

Каждый граф или сам является компонентой связности или распадается на компоненты. Граф, содержащий хотя бы две компоненты связности, называется несвязным. Связный граф состоит из одной компоненты связности.

Граф называется эйлеровым, если он содержит цикл, проходящий через все ребра этого графа по одному разу. Такой цикл называется эйлеровым циклом.

Вот пример эйлерова графа:

А вот пример графа, не являющегося эйлеровым:

Во многих задачах, решаемых с использованием графов, требуется проложить маршрут от одной вершины графа к другой или обойти все его вершины, учитывая те или иные ограничения.

Смысл такой задачи на интуитивном уровне ясен, но требуется уточнить понятия, используемы при решении подобного рода задач.

Прежде всего, уточним термины «маршрут», «цепь», «цикл» и «путь». Эти четыре понятия находятся в следующем соотношении: пути и циклы – это особые виды цепей, цепь – особый вид маршрута.

Маршрут – это последовательность вершин и ребер графа, следуя по которым, можно попасть из одной его вершины в другую.

Цепь – это маршрут без повторяющихся ребер.

Путь – это цепь, все вершины которой (за исключением, быть может, начальной и конечной) различны.

Цикл – это цепь, у которой совпадают начальная и конечная вершины, а все остальные различны.

Можно составить следующие маршруты из А в С в графе G:

М2: А – е2 – Е – е6 – Д – е7 – Д – е6 – Е – е5 – С (не цепь);

М3: А – е1 – B – е3 – C – е5 – Е – е4 – С (цепь, но не путь).

А – е1 – В – е3 – С – е4 – Е – е2 – А;

Граф называют связным, если из каждой его вершины существует путь в любую другую его вершину. Граф, рассмотренный в примере, является, связным. Если удалить из него ребро , то он потеряет связность и распадется на компоненты: одна из компонент будет содержать вершину Д и петлю , вторая компонента – вершины А,В,С,Е, связанные между собой всеми оставшимися ребрами.

Для представления данных в алгоритмах на дискретных структурах часто используются графы, которые называются деревьями.

Деревом называют связный неорграф, не содержащий циклов.

На рис. 6.8 показано, так называемое, корневое дерево. Одна из вершин корневого дерева (вершина 1) выделена, ее называют корнем дерева. Оставшиеся вершины разбиты на поддеревья (поддерево с вершинами 2,5,6 и поддерево 4,7,8,9). Вершины 5,6,3,7,8,9 называют листьями дерева. Несвязный неорграф, компонентами которого являются деревья, называют лесом.

Если граф связный, но не является деревом, в нем всегда можно выделить часть, включающую все вершины и образующую дерево. Такую часть графа называют остовом графа. Если граф несвязен, то можно превратить в дерево каждую его компоненту. Полученная совокупность деревьев носит название остовного леса.

Вообще говоря, в графе можно выделить несколько различных остовов. Каждый из них будет являться деревом, включающим все вершины графа, а следовательно, число ребер любом из остовов будет на единицу меньше числа вершин графа. Если выделен какой-либо остов, то все ребра графа, не вошедшие в этот остов, образуют коостов, соответствующий данному остову.

Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Пусть G связный граф. Тогда остовное дерево графа G (если оно существует) должно содержать n(G) – 1 ребер. Таким образом, любое остовное дерево графа G есть результат удаления из G ровно m(G)-(n(G)-1)=m(G)-n(G)+1 ребер.

На рис. 6.9 показан пример выделения деревьев, остовов и коостовов из графа .

Источник

Деревья и лес.

Граф без циклов называется лесом. Связные компоненты леса называются деревьями.

Связный граф, у которого все ребра ациклические, называется деревом.

· Несвязный граф, компонентами связности которого являются деревья, называется лесом.

· Чтобы простой связный граф был деревом, необходимо и достаточно, чтобы число вершин было больше числа ребер на один.

· Чтобы граф был деревом, необходимо и достаточно, чтобы любые две вершины его соединялись единственным маршрутом.

· Граф будет деревом тогда и только тогда, когда добавление любого нового ребра приводит к появлению ровно одного цикла.

· Удаление любого ребра приводит к несвязному графа

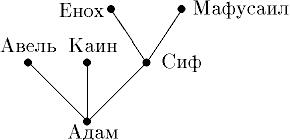
Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярны генеалогические деревья. На рисунке показано библейское генеалогическое дерево

Теория перечисления графов занимается разработкой методов подсчёта числа неизоморфных графов, обладающих тем или иным свойством. Решены задачи о числе графов, орграфов, связных графов, эйлеровых графов и деревьев, содержащих данное число вершин и рёбер. Однако соответствующие результаты для планарных и гамильтоновых графов не получены.

Теорема Кэли (1889): существует ровно n n -2 различных помеченных деревьев с n вершинами.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник

3.1.5. Связность в графах

Рассмотрим вопрос о связности в графах. Пусть G(X) – неори­ентированный граф. Две вершины х_iиx_jназываютсясвязными, если существует цепьSс концами х_iиx_j. ЕслиSпроходит через некото­рую вершинуx_kболее одного раза, то можно удалить цикл в верши­неx_kиз цепиS. Отсюда следует, что вершины, связанные цепью, связаны элементарной цепью.

Неориентированный граф называется связным, если любая па­ра его вершин связана. Отношение связности для вершин графа есть отношение эквивалентности (x_i~x_j, х_j~ х_kx_i~ х_k).

Компонентой связ­ностинеориентирован­ного графаG(X) называ­ется подграф Н_А(А) графаG(X) с множеством вер­шин АXи множеством ребер вG(X), инцидент­ных только вершинам из А, причем ни одна вершинаx_i А не смежна с вершинами из множества Х \ А (рис. 3.12).

Рис. 3.12. Граф с двумя компонентами связности

Ориентированный граф называется сильно связным, если для любой пары вершин найдется путь, соединяющий их.

Компонентой сильной связностиориентированного графаG(X) называется подграф Н_А(А) графаG(Х) (подчиняющийся опре­делению сильно связного графа) с множеством вершин АХ и мно­жеством дуг, имеющих начало и конец в А, причем ни одна из вер­шин х_iА и х_jX\ А не смежны между собой (рис. 3.13).

Рис. 3.13. Ориентированный граф с двумя компонентами сильной связности

Очевидно, что ориентированный граф G(X) сильно связан то­гда и только тогда, когда он имеет одну компоненту связности.

На практике широко используются такие виды графов, как де­ревья и прадеревья.

Деревомназывается конечный связный неориентированный граф, состоящий, по крайней мере, из двух вершин и не содержащий циклов. Такой граф не имеет петель и кратных ребер (рис. 3.14).

Ветвямидерева называются ребра графа, вхо­дящие в дерево.Хордами дереваназываются ребра, входящие в граф, дополнительный к данному дереву.Лагранжевым дере­вомназывается дерево, все ветви которого имеют общую вершину.

Лесом называется несвязный граф, каждая компонента связно­сти которого является деревом.

Прадеревомназывается ориентированный графG(X) с корнем х₀ X, если в каждую вершину х_iх₀(х_iX) заходит ровно одна дуга, а в корень х₀не заходит ни одна дуга. Прадерево не содержит контуров (рис.3.15).

3.1.6. Изоморфизм. Плоские графы

В изображении графа имеется относительно большая свобода в размещении вершин и в выборе формы соединяющих их ребер. По­этому один и тот же граф может быть представлен по-разному (рис. 3.16).

ис. 3.16. Примеры изоморфных графов

Графы G₁(X₁) иG₂(X₂) называютсяизоморфными, если между множествами их вершин существует взаимно однозначное соответ­ствие, сохраняющее смежность вершин. Иначе, если вершины являются смежными (соединены ребрами) в одном из графов, то соответствующие им вершины в другом графе также являются смежными. Если ребра графов ориентированы, то их направление в изоморфных графах также должно соответствовать друг другу.

ГрафG(X) называется плоским, если он может быть изобра­жен на плоскости так, что все пересечения его ребер являются вер­шинами графаG(X) (рис. 3.17).

Рис. 3.17. Примеры плоского (а) и неплоского (б) графов

Источник