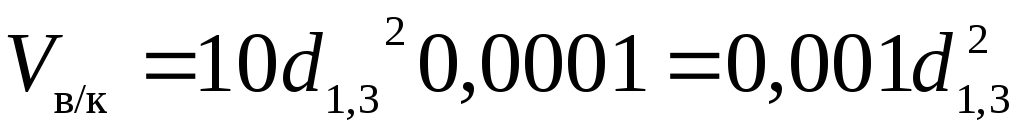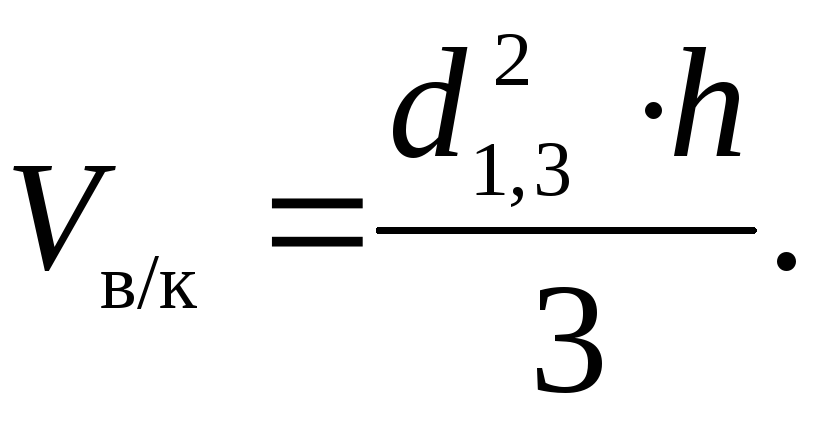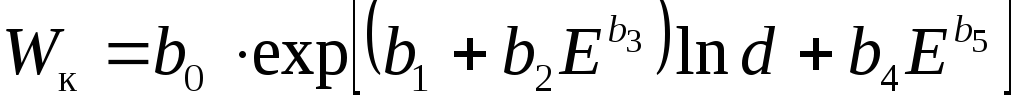Объем кроны дерева формула

Задание 4. Таксация растущего дерева

Объем ствола растущего дерева можно определить по таблицам объемов стволов. На практике для нахождения объема отдельных стволов растущих деревьев чаще всего используют таблицы с двумя входами: по диаметру и высоте. Для определения объема ствола по этим таблицам нужно измерить диаметр на высоте груди и высоту ствола дерева . В таблице на пересечении граф, соответствующих измеренным диаметру и высоте, берут значение искомого объема,

Пример 8. Сосна имеет d_1,3 = 29,8 см; h = 25,3 м. По таблице «Объемы древесных стволов по диаметру и высоте» (табл. 2.1 [1 ] V_в/к = 0,69 м 3 .

Объем ствола можно определить по формулам. Исходя из формулы старого видового числа (17), получим

V_в/к = g_1,3 h f (21)

Эту формулу называют формулой для определения объема ствола растущего дерева.

Пример 9. Диаметр ствола сосны на высоте груди в коре d_1,3= 29,8 см, высота h = 25,3 м, коэффициент формы q₂ = 0,64. По таблицам М. E. Ткаченко находим видовое число f = 0,434.

V_в/к = 0,0697·25,3·0,434 = 0,76 м 3 .

Для приближенного определения объема ствола растущего дерева можно использовать формулы:

; (22)

(23)

В формуле Г. Денцина для стволов сосны с высотой, отличной от 30 м, и ели – 26 м вносят поправку ± 3% на 1 м высоты. При меньших высотах поправку берут со знаком «минус», при больших – со знаком «плюс».

В формуле Н.Н.Дементьева для стволов со значением коэф­фициента формы, отличным от q₂= 0,65, вносят поправку ± 3% на каждое 0,05q₂. При меньших коэффициентах формы поправку берут со знаком «минус», а при больших – со знаком «плюс».

Пример 10. Для сосны d_1,3= 29,8 см, h = 25,3 м, q₂ = 0,64; объемы по формуле Г. Денцина (ф. 22) равен:

V_в/к = 0,001·(29,8) 2 = 0,888;

с учетом поправки 100% – 14,1%= 85,9%;

V_в/к = 0,888 · 0,859 = 0,762 м 3 .

По формуле Н. Н. Дементьева (ф. 23) расчеты соответственно:

V_в/к = =(29,8) 2 · 25,3/3 = 0,749 м 3 .

После определения объема ствола растущего дерева по таблицам и формулам находят отклонения от объема, вычисленного по сложной формуле Губера (см. пример 1), приняв его за истинный. Результаты вычислений сводят в таблицу.

По результатам вычислений абсолютных и относительных отклонений делают заключение о точности определения объема ствола разными способами.

4.2. Таксация кроны дерева

Крона – одна из важнейших составных частей дерева. Она является фотосинтетическим аппаратом растения и без нее невозможно существование дерева как живого организма. Кроме этого, она несет оздоровительную, фильтрующую, регулирующую, поглощающую, защитную и другие функции, Декоративные свойства кроны с древнейших времен использовали в садово-парковом строительстве и озеленении.

При таксации кроны дерева определяют горизонтальную и вертикальную проекции, диаметры кроны на разной высоте, протяженность кроны, ее объем [3, 15, 16].

По форме крона совпадает с геометрическими телами вращения и может быть конусообразной, эллипсовидной, шарообразной, купо­лообразной и др.

Развитие кроны дерева, горизонтальное и вертикальное ее строение, форма зависят от условий роста дерева в лесу. Горизон-тальная проекция кроны может быть флагообразной, округлой и т.д.

К числу основных показателей форм крон, их габитуса можно отнести: поперечник или ширину крон d_к, длину крон l_к, высоту до наибольшей ширины кроны h_dк .

Высота начала кроны h_н.к. устанавливается высотомером при измерении общей высоты дерева h. Длина (протяженность) кроны l_к определяется по формуле

По протяженности кроны деревья группируются в три класса с учетом отношения l_к/h. Если это отношение более ½ (точка начала кроны расположена на высоте ½ и ниже) высоты ствола, то крону следует считать длинной, от ½ до ¼ – средней длины и менее ¼ (точка начала кроны расположена на ¾ и выше) высоты ствола – короткой. Диаметр горизонтальной проекции кроны d_к определяется крономером или путем проектирования ее краев на горизонтальную поверхность, чаще в направлениях С – Ю и В – З с замером рулеткой расстояния и последующим вычислением среднего диаметра кроны. Для вычисления объема кроны также измеряют диаметры кроны на ¼, ½ и ¾ ее длины (l_к), т.е. d_к1, d_к2, d_к3. Эти измерения выполняют специальной палеткой В. П. Кавтунова в относительных показателях. Переход к абсолютным значениям диаметров выполняется путем перемножения их относительных величин на высоту дерева [6]. При расчетах в учебных целях d_к1, d_к2, d_к3 вычисляют через пропорции исходя из диаметра кроны d_к, м. Взаимосвязь размеров крон деревьев с высотами и диаметрами стволов на высоте груди при умеренных рекреационных нагрузках насаждений рассчитывается:

d_к = m₀+m₁d+m₂h+m₃dh. (25)

А длины крон lк, в свою очередь, определяются

где m₀, m₁, m₂,m₃ и r₀, r₁, r₂, r₃ – параметры, зависящие от породы (табл.6); h – высота деревьев, м; d – диаметр стволов на высоте груди, см.

Источник

Параметры моделей взаимосвязей размеров крон деревьев с их высотами и диаметрами на высоте груди

На основании полученных диаметров крон с использованием коэффициентов пропорций определяются диаметры крон d_к1, d_к2, d_к3. Коэффициенты для сосны составят соответственно 0,8; 1,0; 0,7; для ели – 0,8; 0,5; 0,3; для березы – 0,9; 1,0; 0,8; для ольхи – 0,6; 0,9; 1,0; для осины – 0,8; 1,0; 0,9 [2, 3 16].

Объем кроны определяется по формуле

(27)

Для определения процента объема сучьев Р_с у сосны используются следующие формулы А.В.Тюрина и Ф.Корсуня:

Р_с= 4,35 d +5,3. (29)

Для вычисления процента хвои (Р_х)можно использовать формулу М.Т.Семечкиной

Р_х= 15,63 + 1,57d + 0,0005d 2 h + 1,52l_к – 1,21h (30)

где d – диаметр на высоте груди, см; h – высота ствола дерева, м; l_к – протяженность кроны, м. По специальным таблицам, в зависимости от диаметра дерева на высоте груди d_1,3 и высоты дерева h находят вес кроны и её зеленой биомассы.

Установлено, что масса крон и древесной зелени деревьев при умеренных рекреационных нагрузках насаждений характеризуются практически близкими показателями с варьированием 5-15%. Взаимосвязи массы древесной зелени крон деревьев с разрядом высот древостоя описываются уравнением :

, (31)

где b₀, …, b₅ – параметры, зависящие от породы (табл. 7); d – средний диаметр, см; Е – разряд высот древостоя i-го элемента леса.

Аналогичные данные можно получить, используя таблицу Л. Н. Яновского (табл.8).

Источник