Обход двоичного дерева ширину

Поиск в ширину на Python

Двоичные деревья вечны. По крайней мере, так думают технические менеджеры, занимающиеся наймом разработчиков. И когда на техническом собеседовании вас просят решить задачу, касающуюся двоичных деревьев, первое, что интервьюер захочет знать, — в ширину или в глубину?

В чем разница?

Когда говорят о поиске в ширину (Breadth First Search, BFS) и глубину (Depth First Search, DFS), имеется в виду порядок обхода узлов двоичного дерева. При обходе в глубину вы сначала опускаетесь к низу дерева, а потом идете в сторону, а при обходе в ширину — наоборот, начинаете с корня и спускаетесь сначала к его узлам-потомкам, обходите их, потом спускаетесь к потомкам потомков, обходите их, и так далее.

Если взять в качестве примера двоичное дерево на этом рисунке, при BFS-подходе порядок обхода узлов будет следующим: 1, 2, 3, 4, 5.

В случае с DFS возможны разные варианты последовательности посещения узлов. Все зависит от того, будет это прямой, обратный или центрированный обход. Например, прямой обход выдаст 1, 2, 4, 5, 3. Мы разбирали эти три типа обхода в статье «Обход двоичного дерева на Python».

Реализация поиска в ширину на Python

Давайте посмотрим, как сделать BFS на Python. Начнем с определения нашего класса TreeNode. В нем должны быть только значение и левый и правый указатели.

class TreeNode: def __init__(self, value): self.value = value self.left = None self.right = None

1. Стратегия

Вот как мы будем обходить узлы:

1. Найдем высоту дерева от корня до самого дальнего листа.
2. В цикле переберем все уровни (заканчивая верхушкой).
3. Обойдем каждый уровень, выводя все узлы.

2. Поиск высоты дерева

Чтобы обойти каждый уровень, нам нужно сначала узнать, сколько всего уровней в дереве. Для этого мы напишем специальный метод.

Да, вы угадали: метод будет рекурсивным, как и большинство методов для обхода двоичных деревьев. Давайте подумаем, каким будет базовый случай. Самый простой вариант — когда у нас нулевой корень. В этом случае высота — 0. Вам может показаться, что простейший случай — узел без потомков, но тогда нам придется проверять, есть ли потомки, а это уже увеличивает сложность.

def height(node): if not node: return 0

Что дальше? Нам нужно обойти левую и правую половину дерева. Мы будем вызывать метод height() для этих половин и сохранять в две переменные: l_height и r_height .

def height(node): if not node: return 0 l_height = height(node.left) r_height = height(node.right)

Какую высоту мы вернем: левую или правую? Конечно, большую! Поэтому мы берем max() обоих значений и возвращаем его. Не забудьте добавить 1 для текущего узла.

def height(node): if not node: return 0 l_height = height(node.left) r_height = height(node.right) return max(l_height, r_height) + 1

3. Перебор уровней в цикле

Теперь, когда у нас есть высота, мы можем приступить к написанию метода для обхода дерева в ширину. Единственный аргумент, который этот метод будет принимать, — корневой узел.

Затем нам нужно получить нашу высоту.

def breadth_first(root): h = height(root)

Наконец, мы перебираем в цикле высоту дерева. На каждой итерации мы будем вызывать вспомогательную функцию — print_level() , которая принимает узел root и уровень.

def breadth_first(root): h = height(root) for i in range(h): print_level(root, i)

4. Обход дерева

Мы будем обходить каждый уровень отдельно, выводя все узлы на нем. Тут нам пригодится наша вспомогательная функция. Она принимает два аргумента: корень и текущий уровень.

def print_level(root, level):

В этом методе номер уровня определяется индексом i цикла for . Чтобы обойти все дерево, мы будем рекурсивно двигаться по уровням, уменьшая i , пока не достигнем уровня 0. Когда достигнем, это будет означать, что теперь можно выводить узлы на экран.

Наш базовый случай — когда корень — null . Этот метод только выводит дерево на экран и ничего не возвращает, поэтому в базовом случае будет просто return .

def print_level(root, level): if not root: return

Далее, если наш уровень — 0 (то есть интересующий нас уровень), нам нужно вывести значение этого узла.

def print_level(root, level): if not root: return if level == 0: print(root.value)

Наконец, если номер уровня больше нуля, это означает, что нам нужно продолжить обход дерева. Мы вызываем наш рекурсивный метод для левой и правой половин дерева. Не забудьте отнять единицу от level в обоих вызовах функции.

def print_level(root, level): if not root: return if level == 0: print(root.value) elif level > 0: print_level(root.left, level - 1) print_level(root.right, level - 1)

Вот и все! Нам пришлось создать три разных метода, но в конечном итоге мы можем обойти дерево в ширину.

5. Тестирование

Для начала давайте создадим дерево, используя наш класс TreeNode .

Теперь нужно заполнить оставшуюся часть дерева. При помощи следующих строк кода мы приведем дерево к тому виду, что изображен на схеме.

tree.left = TreeNode(2) tree.right = TreeNode(3) tree.left.left = TreeNode(4) tree.left.right = TreeNode(5)

Наконец, запускаем наш метод.

Ожидаемый результат: 1, 2, 3, 4, 5 . Мы успешно обошли дерево!

Источник

Бинарное дерево. Способы обхода и удаления вершин

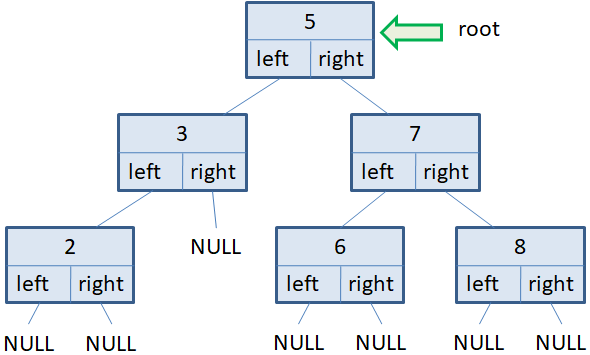
Давайте представим, что у нас имеется следующее двухуровневое бинарное дерево: На корневую вершину ведет указатель root. Создадим еще один вспомогательный указатель p на эту же вершину:

Изначально в списке только одна корневая вершина. Сформируем два цикла: первый будет работать, пока список вершин не пуст, то есть, пока в дереве имеются узлы текущего уровня; а второй будет перебирать вершины текущего уровня, выводить информацию на экран и формировать список следующего уровня:

while v: vn = [] for x in v: print(x.data) if x.left: vn += [x.left] if x.right: vn += [x.right] v = vn

В результате, сначала будет выведено значение 7 корневого узла. Затем, сформирован список vn из двух узлов следующего уровня в порядке слева-направо. После этого списку v присваивается новый сформированный список vn следующего уровня и на следующей итерации цикла while во вложенном цикле for будут перебираться уже вершины первого уровня. На экран выведутся значения 2 и 5. Снова сформируется список vn из вершин следующего второго уровня. И на следующей итерации цикла while будут выведены значения 3, 4 и 6. После этого список vn окажется пустым, следовательно, список v также будет пустой и цикл while завершит свою работу. Вот пример реализации алгоритма перебора вершин бинарного дерева в ширину в самом простом варианте. При этом мы обходим по всем узлам дерева ровно один раз.

Алгоритм обхода в глубину

Следующий тип алгоритмов – это обход дерева в глубину. Здесь мы проходим по определенной ветви до листовой вершины. Лучше всего показать этот ход на конкретном примере. Пусть у нас то же самое бинарное дерево. Начальная вершина, как всегда, корневая (root). Затем, мы должны для себя решить, по какой из двух ветвей идти в первую очередь, а по какой – во вторую. Я решил обойти дерево сначала по левой ветви, а затем, с возвратами проходить правые ветви. Это можно реализовать следующей рекурсивной функцией:

def show_tree(self, node): if node is None: return self.show_tree(node.left) print(node.data) self.show_tree(node.right)

Как она работает? Мы начинаем двигаться от корневого узла. Если он существует, то вызывается та же самая функция для левого узла. В результате, мы как бы попадаем в ту же самую функцию, только параметр node теперь является ссылкой на узел со значением 3. Здесь выполняется та же самая проверка: если узел существует, то по рекурсии мы снова переходим к следующему левому узлу. Это узел со значением 2. Снова делается проверка на его существование и, так как он существует, переходим к следующему левому узлу. Теперь параметр node принимает значение None (на рисунке NULL), рекурсия завершается и мы возвращаемся к прежнему вызову с параметром node узла 2. Это значение отображается на экране и делается попытка пройти по правой ветви. Так как справа объектов нет, то вызов текущей функции завершается и мы попадаем в функцию уровнем выше с параметром node на узел 3. Это значение 3 выводится на экран и делается попытка пройти по правой ветви. Ее нет, поэтому мы возвращаемся на уровень выше, то есть, к корневому узлу со значением 5. Это значение выводится на экран и далее мы переходим к правой вершине 7. Снова вызывается рекурсивная функция с параметром node на узел 7 и делается попытка пройти по левой ветви. Там имеется вершина со значение 6. Она выводится на экран с возвратом к функции узла 7. Затем, отображаем эту семерку на экран и переходит к левому узлу со значением 8. Это значение также отображается, после чего все вызовы рекурсивных функций завершаются. В результате мы на экране увидим следующие значения, записанные в вершинах бинарного дерева: 2, 3, 5, 6, 7, 8 Вы можете подумать, что такой возрастающий порядок значений получился чисто случайно. Однако нет. Если у нас имеется бинарное дерево сформированное по правилу добавления меньших значений в левую ветвь, а больших – в правую, то при обходе дерева в глубину в порядке: левое поддерево (L); промежуточная вершина (N); правое поддерево (R) всегда будет образовываться возрастающая последовательность чисел. Сокращенно такой алгоритм в глубину получил название LNR и относится к симметричному типу обхода. А если пройти сначала по правой ветви, затем вывести значение промежуточной вершины, а после пройти по левой ветви, то получим убывающую последовательность значений в бинарном дереве: 8, 7, 6, 5, 3, 2 Такой алгоритм сокращенно называется RNL и также является одним из видов симметричного обхода. Комбинируя различные варианты обхода и отображения значений вершин можно получать самые разнообразные вариации алгоритмов обхода в глубину.

Удаление вершин бинарного дерева

Теперь, когда мы с вами подробно разобрались в способах формирования бинарного дерева и алгоритмами обхода его вершин, остался один важный вопрос, связанный с удалением его узлов. Здесь возможны несколько типовых исходов.

Удаление листовых вершин

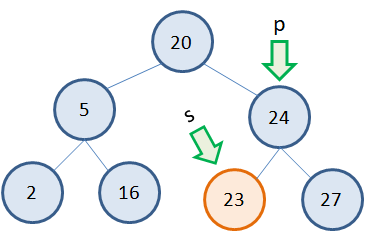
Самый простой случай, когда удаляется листовой узел дерева. Предположим, что это узел 23: Тогда, нам достаточно получить указатель p на родительский узел и указатель s на удаляемый узел. Сделать это очень просто, запоминая при обходе дерева предыдущую (родительскую) вершину и текущую. После этого ссылку, ведущую на удаляемый узел следует приравнять NULL и освободить память из под узла s:

Удаление узла с одним потомком

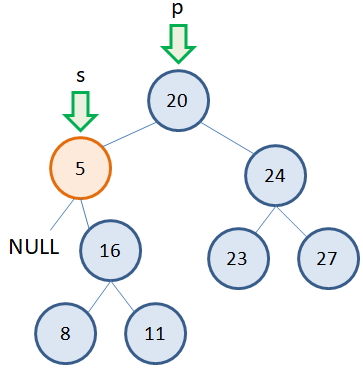
Также относительно просто обстоит ситуация, когда у удаляемого узла имеется один потомок (слева или справа). Например, нам нужно удалить узел 5, у которого один потомок справа: Здесь мы также должны иметь два указателя: p – на родительскую вершину; s – на удаляемую вершину. Затем, исключаем из дерева удаляемую вершину 5, меняя связь от родительской вершины 20 к вершине 16 (которая идет после удаляемой):

Причем, ситуация принципиально не меняется, если у удаляемой вершины один правый или левый потомок. Алгоритм удаления таких вершин работает похожим образом.

Удаление узла с двумя потомками

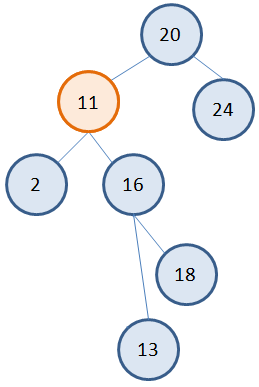
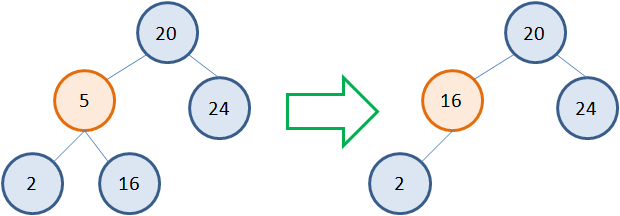
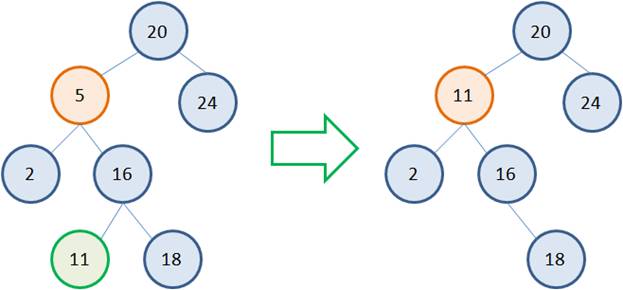
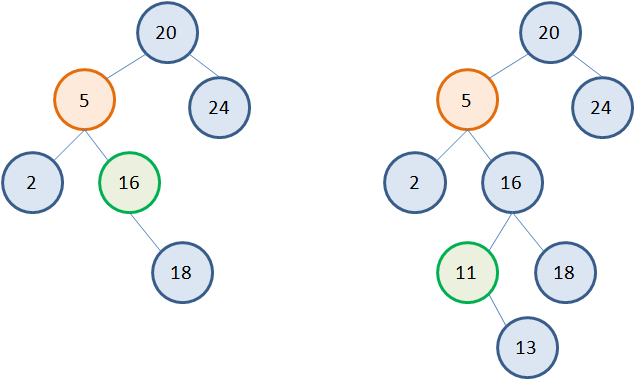
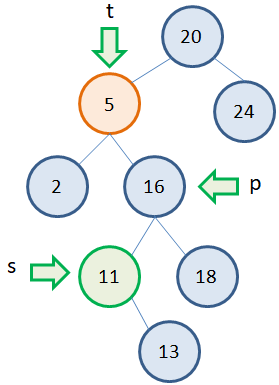
Несколько сложнее обстоит дело, когда у удаляемой вершины два потомка. Общая идея здесь такая. Сам узел не удаляется, меняется только его значение на новое. А новое берется как наименьшее из правой ветви. Например, если мы хотим удалить узел 5, то следует взять наименьшее значение 16 из правого поддерева. Записать его вместо 5, а листовой узел 16 просто удалить: Но это если справа расположен листовой узел. А что если справа имеется полноценное поддерево с множеством вершин? Как быть в такой ситуации? По сути, также. Идея алгоритма остается прежней. Выбираем узел с наименьшим значением 11 в правом поддереве, заменяем 5 на 11 и удаляем листовой узел 11: Но вершина с наименьшим значением в правом поддереве не всегда является листовой. Возможны и такие ситуации: Однако можно заметить, что у узла с наименьшим значением может быть только один потомок справа. А значит, его удаление будет выполняться по алгоритму удаления вершин с одним потомком. Например, рассмотрим второе дерево. Нам потребуется три указателя: t – на удаляемую вершину (то есть, вершину, у которой будет меняться значение); s – на вершину с наименьшим значением в правом поддереве; p – на родительскую вершину для вершины s: Затем, мы меняем значение вершины 5 на 11:

В результате получаем дерево: Вот основные типовые варианты удаления вершин в бинарном дереве:

• удаление листового узла;
• удаление узла с одним потомком (правым или левым);
• удаление узла с двумя потомками.

На следующем занятии, в качестве примера, реализуем бинарное дерево на языке Python, чтобы вы во всех деталях понимали принцип его работы. Курс по структурам данных: https://stepik.org/a/134212

Источник