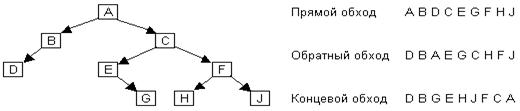
3.7. Обходы бинарных деревьев и леса
Многие алгоритмы работы с бинарными деревьями основаны на последовательной обработке узлов дерева. Если для линейного списка последовательность обработки элементов очевидна (в однонаправленных списках только в прямом, в двунаправленных — в прямом и обратном направлении), то в бинарном дереве имеется гораздо больше возможностей из-зи наличия ветвления. В связи с этим вводится понятие обхода дерева. При обходе дерева каждый узел посещается только один раз, при этом узлы выстраиваются в определённую линейную последовательность узлов, т.е. можно говорить о предыдущем и следующем узле.
Понятие обхода вводится для любых деревьев, однако удобнее начать с обхода бинарных деревьев ввиду простоты и универсальности.
Наиболее известны и практически важны 3 способа прохождения, которые отличаются порядком и направлением обхода бинарного дерева. К сожалению, в литературе встречается довольно много различных названий для данных обходов, что порождает некоторую путаницу. В таблице 3.4 приведены основные названия (верхняя строка) и алгоритмы рекурсивного прохождения узлов дерева для каждого способа (нижняя строка).
Рекурсивное прохождение бинарного дерева.
Postorder(постфиксный)
3. Пройти правое поддерево
3. Пройти правое поддерево
2. Пройти правое поддерево
Прямой порядок прохождения означает обход в направлении сверху-вниз, когда после посещения очередного разветвления продолжается прохождение вглубь дерева, пока не пройдены все потомки достигнутого узла. По этой причине прямой порядок прохождения часто называют нисходящим, или прохождением в глубину. Прямой порядок используется в представлении дерева в форме вложенных скобок (левое скобочное представление), в виде уступчатого списка или десятичной классификации Дьюи. В геналогических терминах прямой порядок прохождения дерева отражает династический порядок престолонаследования, когда титул передается старшему потомку.
При центрированном (симметричном) проядке дерево проходится слева направо. Такой порядок используется, например, при обходе бинарного дерева поиска, порождая упорядоченную последовательность значений. Подробнее об этом будет рассказано в главах, посвященных сортировке и поиску.
Если применяется концевой порядок прохождения, то получается обход дерева снизу-вверх, когда в момент посещения любого узла все его потомки уже пройдены, а корень дерева проходится последним. Из-за этой особенности обхода, концевой порядок называют восходящим, или обратным относительно прямого.
Иногда используется еще один способ обхода бинарного дерева обход в горизонтальном порядке (в ширину). При таком способе узлы бинарного дерева проходятся слева направо, уровень за уровнем от корня вниз (поколение за поколением от старших к младшим).
Очередность обработки узлов
Источник
Обход дерева – центрированный (inorder), прямой (preorder) и обратный (postorder) (три основных способа обхода)
Обход дерева означает посещение каждого узла дерева. Например, вы можете добавить все значения в дерево или найти самое большое. Для всех этих операций вам необходимо будет посетить каждый узел дерева. Линейные структуры данных, такие как массивы, стеки, очереди и связанный список, имеют только один способ чтения данных. Но иерархическая структура данных, такая как дерево, может проходить разными способами. Давайте подумаем о том, как мы можем прочитать элементы дерева на изображении, показанном выше. Начиная сверху, слева направо
Начиная снизу, слева направо
Хотя этот процесс в некотором роде прост, он не учитывает иерархию дерева, а только глубину узлов. Вместо этого мы используем методы обхода, которые учитывают базовую структуру дерева, то есть
Помните, что нашей задачей является посещение каждого узла, поэтому нам нужно посетить все узлы в поддереве, посетить корневой узел и также посетить все узлы в правом поддереве.
В зависимости от порядка, в котором мы это делаем, может быть три типа обхода .
Центрированный тип обхода (Inorder traversal)
- Сначала посетите все узлы в левом поддереве
- Затем корневой узел
- Посетите все узлы в правом поддереве
inorder(root->left) display(root->data) inorder(root->right)Прямой тип обхода (Preorder traversal)
- Посетите корневой узел
- Посетите все узлы в левом поддереве
- Посетите все узлы в правом поддереве
display(root->data) preorder(root->left) preorder(root->right)Обратный тип обхода (Postorder traversal)
- посетить все узлы в левом поддереве
- посетить корневой узел
- посетить все узлы в правом поддереве
postorder(root->left) postorder(root->right) display(root->data)Давайте визуализируем центрированный тип обхода (inorder traversal). Начнем с корневого узла.
Сначала мы проходим левое поддерево. Мы также должны помнить, что нужно посетить корневой узел и правое поддерево, когда дерево будет готово.
Давайте поместим все это в стек, чтобы мы помнили.
Теперь перейдем к поддереву, указанному на вершине стека.
Опять же, мы следуем тому же правилу центрированного типа (inorder)
Left subtree -> root -> right subtreeПройдя левое поддерево, мы остаемся с
Поскольку у узла "5" нет поддеревьев, мы печатаем его напрямую. После этого мы печатаем его родительский узел «12», а затем правый дочерний «6».
Поместить все в стек было полезно, потому как теперь, когда левое поддерево корневого узла было пройдено, мы можем распечатать его и перейти к правому поддереву.
После прохождения всех элементов, центрированный тип обхода (inorder traversal) выглядит так:
Нам не нужно создавать стек самостоятельно, потому что рекурсия поддерживает для нас правильный порядок.
Полный код для центрированного (inorder), прямого (preorder) и обратного (postorder) типа обхода на языке программирования C размещен ниже:
#include #include struct node < int data; struct node* left; struct node* right; >; void inorder(struct node* root)< if(root == NULL) return; inorder(root->left); printf("%d ->", root->data); inorder(root->right); > void preorder(struct node* root)< if(root == NULL) return; printf("%d ->", root->data); preorder(root->left); preorder(root->right); > void postorder(struct node* root) < if(root == NULL) return; postorder(root->left); postorder(root->right); printf("%d ->", root->data); > struct node* createNode(value)< struct node* newNode = malloc(sizeof(struct node)); newNode->data = value; newNode->left = NULL; newNode->right = NULL; return newNode; > struct node* insertLeft(struct node *root, int value) < root->left = createNode(value); return root->left; > struct node* insertRight(struct node *root, int value)< root->right = createNode(value); return root->right; > int main()< struct node* root = createNode(1); insertLeft(root, 12); insertRight(root, 9); insertLeft(root->left, 5); insertRight(root->left, 6); printf("Inorder traversal \n"); inorder(root); printf("\nPreorder traversal \n"); preorder(root); printf("\nPostorder traversal \n"); postorder(root); >Вывод кода будет выглядеть так:
Inorder traversal 5 ->12 ->6 ->1 ->9 -> Preorder traversal 1 ->12 ->5 ->6 ->9 -> Postorder traversal 5 ->6 ->12 ->9 ->1 ->
Рекомендуем хостинг TIMEWEB
Стабильный хостинг, на котором располагается социальная сеть EVILEG. Для проектов на Django рекомендуем VDS хостинг.
Рекомендуемые статьи по этой тематике
По статье задано0 вопрос(ов)
Вам это нравится? Поделитесь в социальных сетях!
Источник
Обход бинарного дерева
Бинарное дерево определяется как конечное множество узлов, которое или пусто, или состоит из корня и двух непересекающихся бинарных деревьев, называемых левым и правым поддеревьями корня. Отметим, что деревья на рисунке слева различны, так как в одном случае пусто левое поддерево, а в другом правое.
Узел бинарного дерева может быть представлен структурой:
NODE *Llink; // указатель на левого сына
NODE *Rlink; // указатель на правого сына
Для работы с древовидными структурами имеется множество алгоритмов, и многие из них используют одну и ту же идею, а именно идею прохождения или обхода дерева. Обход дерева подразумевает такой порядок работы с его узлами, для которого каждый из них посещается точно один раз. Для обхода бинарного дерева могут быть использованы три способа, определяемых рекурсивно.
3. Обойти правое поддерево
3. Обойти правое поддерево
2. Обойти правое поддерево
 |
Рис. 22 Варианты обхода бинарного дерева.
На рис. 23 изображено бинарное дерево и порядок следования его узлов для различных методов обхода.
Рис 23. Бинарное дерево и варианты его обхода
Ниже приводится текст рекурсивной функции, выполняющей обход дерева в прямом порядке.
void DirectBypass(NODE *Root)
// Root – указатель на корень дерева
if(Root==NULL) return; // дерево пусто
Обработка(Root); // делаем то, что нужно с узлом
DirectBypass(Root->Llink); // пройти левое поддерево
DirectBypass(Root->Rlink); // пройти левое поддерево
Обратный и концевой обходы отличаются только местоположением оператора Обработка(Root) среди остальных.
Идея реализации алгоритма с "ручным" ведения стека (это может потребоваться, если язык не допускает рекурсии) заключается в том, что мы запоминаем в стеке историю спуска по левым ветвям дерева для того, чтобы впоследствии можно было вернуться и обработать оставшиеся узлы. Ниже приведен текст функции, выполняющей обход в обратном порядке.
const int MAXSTACK=50;
void InverseBypass(NODE *Root)
// Нерекурсивный обход бинарного дерева
NODE *stack[MAXSTACK];
int v=0; // указатель на вершину стека
// спускаемся по левым ветвям, запоминая историю в стеке
// взять узел из стека
// переходим к правому поддереву
Рассмотрим две конкретные задачи, решаемые с помощью обхода дерева.
Задача 1. Копирование бинарного дерева
Для решения задачи естественно использовать прямой обход с тем, чтобы узел – отец создавался раньше, чем сыновья.
NODE *CopyBinTree(NODE *Root)
// функция имеет указатель на корень
// дерева – оригинала в качестве аргумента
// и возвращает указатель на корень дерева – копии
if(Root==NULL) return NULL;
// создадим корень в копии
NODE *RootCopy=new NODE;
// левый и правый сыновья в дереве – копии являются
// копиями левого и правого поддеревьев корня в оригинале
RootCopy->Llink=CopyBinTree(Root->Llink);
RootCopy->Rlink=CopyBinTree(Root->Rlink);
Return RootCopy;
Задача 2. Вычисление значения выражения, заданного деревом.
В качестве примера рассмотрим выражение ((2+3)*(7-4))/3. Порядок вычисления выражения можно изобразить в виде дерева на рис. 24.
 |
Узел дерева в поле данных содержит либо число, либо символ операции. Если узел содержит число, то это операнд, а если операцию, то значения левого и правого поддеревьев суть её операнды. Вычисление естественно выполнять в порядке концевого обхода, поскольку для того, чтобы выполнить операцию, надо знать её операнды. Структура узла имеет вид:
const int OPERATION=0; // признак: узел содержит операцию
const int NUMBER=1; // признак: узел содержит число
char Operation; // символ операции
float Number; // число
int Tag; // может принимать значения OPERATION или NUMBER
UZEL *Left, *Right; // указатели на сыновей
Приведенная ниже функция вычисляет значение выражения, заданного деревом.
float TreeValue(UZEL *Root)
float Result;
if(Root->Tag==NUMBER) return Root->Number;
// в узле операция. Найдем её операнды
float x=TreeValue(Root->Left); // левый операнд
float y=TreeValue(Root->Right); // правый операнд
// выполним операцию
case ' + ':
case ' * ':
case ' / ':
return Result;
Источник