Общие сведения дерево связей

АЛГОРИТМЫ И СТРУКТУРЫ ДАННЫХ

Электронный учебный материал для студентов всех специальностей факультета Прикладная информатика Кубанского государственного аграрного университета

• Главная
• Лекции
  • курс лекций для ИСиТ
  • Курс лекций для БИ
  • Курс лекций для ПИ
  • Презентации
  • Темы лабораторных работ
  • Темы курсовых работ
  • Пример выполнения курсовой работы
  • Вопросы к экзамену ПИ
  • Вопросы к экзамену ИСиТ
  • Вопросы к экзамену БИ

  Поиск

  Об авторах

  Курс разработан на кафедре Компьютерных технологий и систем Кубанского государственного аграрного унивеситета. Авторами являются заведующий кафедрой, доктор технических наук, профессор Лойко Валерий Иванович и доцент кафедры, кандидат физико-математических наук Лаптев Сергей Владимирович.

  Основные цели сайта

  Сайт предназанчен для максимально эффективного и быстрого доступа ко всем материалам курса «Алгоритмы и структуры данных», имеющимся на кафедре компьютерных технологий и систем КубГАУ. Основной задачей его создания является повышения эффективности освоения дисциплины студентами и всеми желающими.

  Нелинейные связанные структуры

  Двусвязный список может быть нелинейной структурой данных, если вторые указатели задают произвольный порядок следования элементов.

  

  LST1 — указатель на начало первого списка (ориентированного указателемями PTR1). Он линейный и состоит из 5-и элементов.

  Второй список образован из этих же самых элементов, но в произвольной последовательности. Началом 2-го списка является 3-й элемент, а концом 2-ой элемент.

  В общем случае элемент списочной структуры может содержать сколь угодно много указателей, то есть может указывать на любое количество элементов.

  Можно выделить 3 признака отличия нелинейной структуры:

  1) Любой элемент структуры может ссылаться на любое число других элементов структуры, то есть может иметь любое число полей-указателей.

  2) На данный элемент структуры может ссылаться любое число других элементов этой структуры.

  3) Ссылки могут иметь вес, то есть подразумевается иерархия ссылок.

  Пример моделирования с помощью нелинейного списка

  Пусть имеется дискретная система, в графе состояния которой узлы — это состояния, а ребра — переходы из состояния в состояние.

  

  Входной сигнал в систему это X. Реакцией на входной сигнал является выработка выходного сигнала Y и переход в соответствующее состояние.

  Граф состояния дискретной системы можно представить в виде двусвязного нелинейного списка. При этом в информационных полях должна записываться информация о состояниях системы и ребрах. Указатели элементов должны формировать логические ребра системы

  Для реализации вышесказанного:

  1) должен быть создан список, отображающий состояния системы (1, 2, 3);

  2) должны быть созданы списки, отображающие переходы по ребрам из соответствующих состояний.

  Реализация графа в виде нелинейного списка можно представить рисунка ниже:

  

  В общем случае при реализации многосвязной структуры получается сеть.

  Рекурсивные структуры данных.

  Рассмотрим рекурсивные алгоритмы и рекурсивные структуры данных.

  Рекурсия — процесс, протекание которого связано с обращением к самому себе (к этому же процессу).

  Пример рекурсивной структуры данных — структура данных, элементы которой являются такими же структурами данных

  

  Деревья

  Дерево — нелинейная связанная структура данных

  Дерево характеризуется следующими признаками:

  — дерево имеет один элемент, на который нет ссылок от других элементов. Этот элемент называется корнем дерева;

  — в дереве можно обратиться к любому элементу путем прохождения конечного числа ссылок (указателей);

  — каждый элемент дерева связан только с одним предыдущим элементом.

  Любой узел дерева может быть промежуточным либо терминальным (листом). На рисунке промежуточными являются элементы M1, M2; листьями — A, B, C, D, E. Характерной особенностью терминального узла является отсутствие ветвей.

  Количество ветвей, растущих из узла дерева, называется степенью исхода узла (на рисунке для M1 степень исхода 2, для М2 — 3).

  Для описания связей между узлами дерева применяют также следующую терминологию: М1 — “отец” для элементов А и В. А и В — “сыновья” узла М1.

  1) если максимальная степень исхода равна m, то это — m-арное дерево;

  2) если степень исхода равна либо 0, либо m, то это — полное m-арное дерево;

  3) если максимальная степень исхода равна 2, то это — бинарное дерево;

  4) если степень исхода равна либо 0, либо 2, то это — полное бинарное дерево.

  Наиболее удобно деревья представлять в памяти ЭВМ в виде связанных списков. Элемент списка должен содержать информационные поля, в которых могут содержаться значение ключа узла и другая хранимая информация, а также поля-указатели, число которых равно степени исхода.

  

  Бинарные деревья

  Согласно представлению деревьев в памяти ЭВМ каждый элемент бинарного дерева является записью, содержащей четыре поля. Значения этих полей — соответственно ключ записи, текст записи, ссылка на элемент влево – вниз и ссылка на элемент вправо – вниз.

  Бинарные деревья являются наиболее используемой разновидностью деревьев.

  Формат элемента бинарного дерева представлен на рисунке ниже

  

  Функция создания элемента бинарного дерева V = MakeTree (key, rec)

  V — указатель на создаваемый элемент динамической структуры

  Алгоритм функции Maketree(key,rec)

  Операция V = MakeTree(Key, Rec) — создает элемент (узел дерева) с двумя указателями и двумя полями (ключевым и информационным) .

  Упорядочное бинарное дерево

  В упорядоченном бинарном дереве левый сын имеет ключ меньший, чем у отца, а значение ключа правого сына больше значения ключа отца.

  Построим бинарное дерево из следующих элементов: 50, 46, 61, 48, 29, 55, 79.

  

  Получено идеально сбалансированное дерево — дерево, в котором левое и правое поддеревья имеют уровни, отличающиеся не более чем на единицу.

  Сведение m-арного дерева к бинарному

  1.В любом узле дерева отсекаются все ветви, кроме крайней левой, соответствующей старшим сыновьям.

  2.Соединяются горизонтальными линиями все сыновья одного родителя.

  3. Старшим (левым) сыном в любом узле полученной структуры будет узел, находящийся под данным узлом (если он есть).

  Графическое пояснение алгоритма

  

  Реализация полученного бинарного дерева с помощью нелинейного двусвязного списка можно представить в иде рисунка ние

  

  • Лекция 1. Понятие структуры данных. Статические структуры данных
  • Лекция 2. Статические и полустатические структуры данных
  • Лекция 3. Полустатические очереди
  • Лекция 4. Понятие динамических структур данных. Связные списки
  • Лекция 5. Реализация стеков и очередей с помощью односвязных списков
  • Лекция 6. Односвязный список как самостоятельная структура данных.
  • Лекция 7. Нелинейные связанные структуры. Деревья. Бинарные деревья
  • Лекция 8. Основные операции с деревьми
  • Лекция 9. Поиск. Классификация основных видов поиска
  • Лекция 10. Методы оптимизации поиска
  • Лекция 11. Дерево оптимального поиска
  • Лекция 12. Поиск по бинарному дереву со вставкой
  • Лекция 13. Поиск по бинарному дереву с удалением
  • Лекция 14. Понятие сортировки. Внутренняя и внешняя сортировки
  • Лекция 15. Прямые методы сортировки.
  • Лекция 16. Улучшенные методы сортировки. Сортировка Шелла
  • Лекция 17. Быстрая сортировка. Оценка эффективности различных методов сортировки

  Источник

  Дерево связей и аффилированность

  Рассказываем о важном графическом инструменте, с помощью которого вы наглядно увидите связи своих контрагентов.

  Дерево связей и аффилированность

  Рассказываем о важном графическом инструменте, с помощью которого вы наглядно увидите связи своих контрагентов.

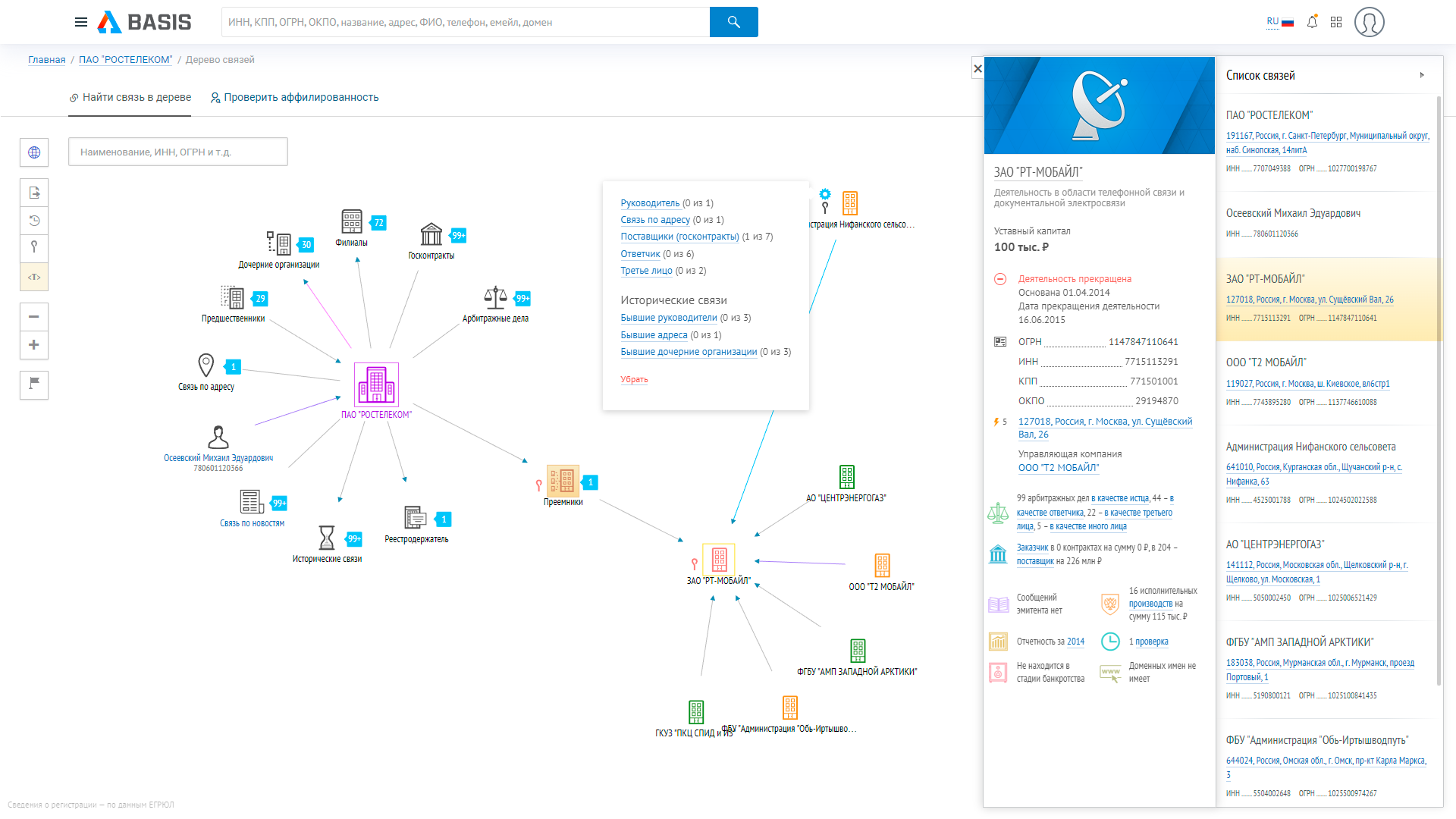
  Что такое «Дерево связей»

  «Дерево связей» — это инструмент, который позволяет быстро увидеть все связи компании без анализа каждого раздела в карточке компании. Оно схематично отображает взаимодействие между связанными как-либо организациями и должностными лицами. Раскрывая интересующие вас типы связей, вы сможете получить информацию о структуре компании (филиалы и дочерние организации), об исторических связях (по адресу), связях по арбитражным делам, а также деятельности совладельцев и руководителей.

  Всего на схеме могут быть следующие типы связей:

  

  • Филиалы
  • Дочерние организации
  • Преемники
  • Предшественники
  • Реестродержатели
  • Госконтракты
  • Арбитражные дела
  • Исторические связи
  • Связь по руководителю
  • Связь по адресу
  • Совладельцы (юридические лица)
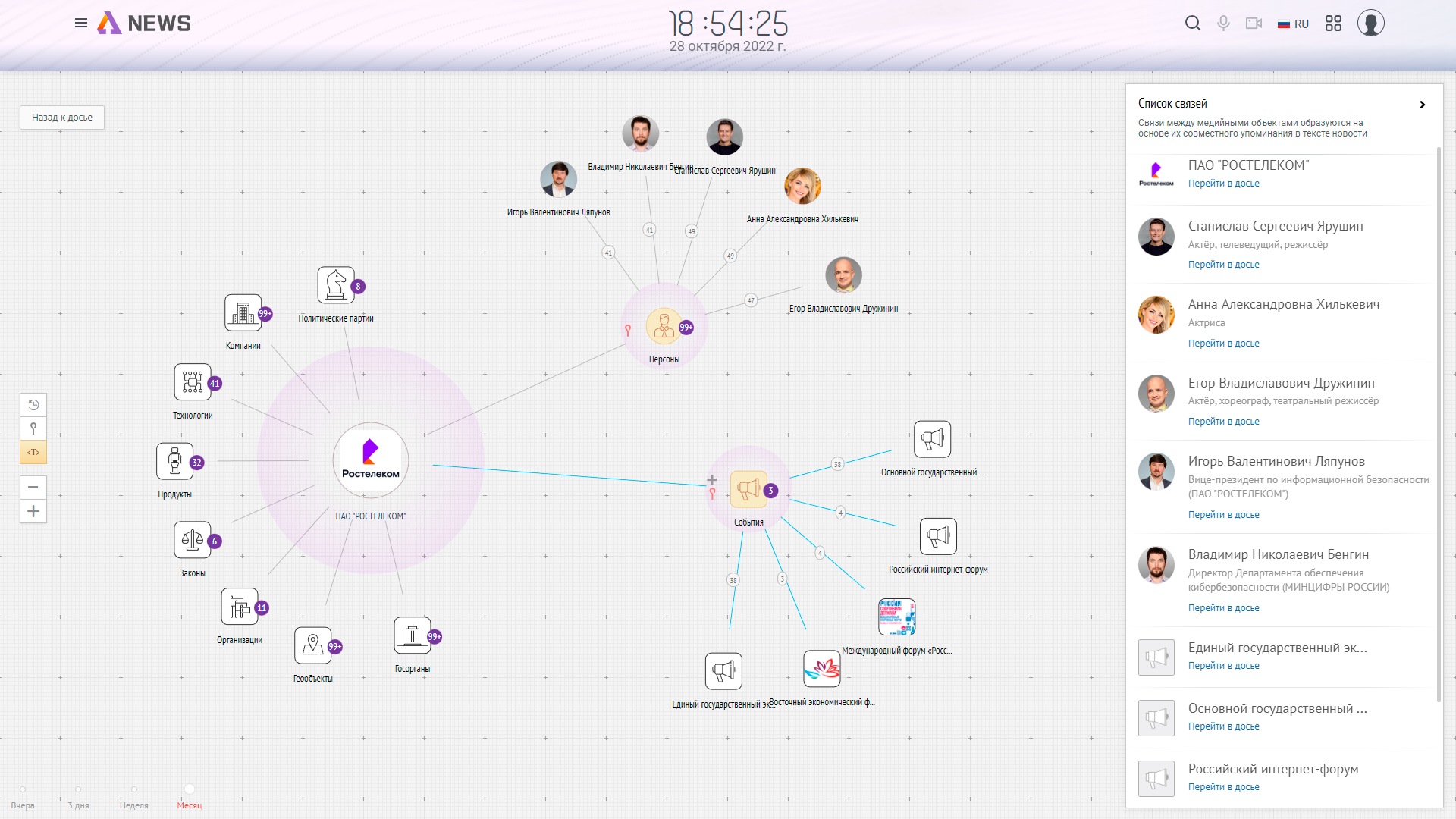
  • Связь по новостям

  Связь по новостям позволяет перейти в агрегатор новостей Seldon.News, где вы можете изучить досье компании — новости, в которых она упоминается. Это поможет вам собрать репутационную среду в СМИ и разобраться с тональностью и предметом упоминаний.

  

  Дерево связей формируется для всех типов российских бизнес-субъектов: юридические лица, индивидуальные предприниматели и аккредитованные филиалы и представительства.

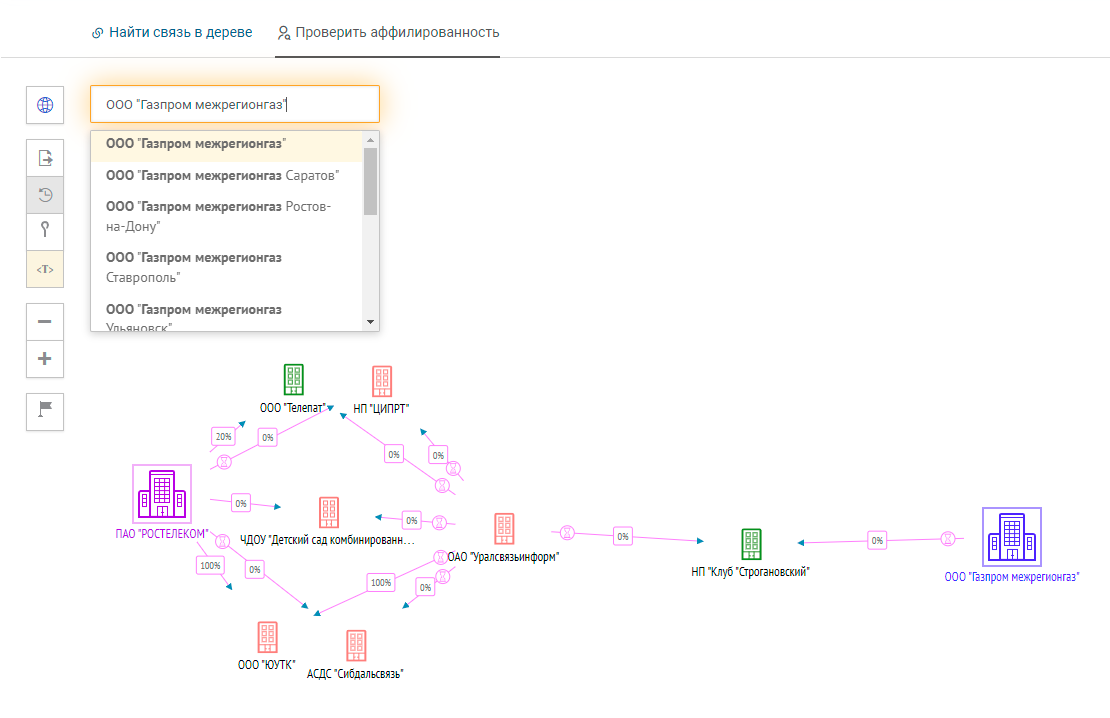
  Как проверить аффилированность

  Перед началом сотрудничества каждой компании РФ следует проверить контрагента для соблюдения «должной осмотрительности». Взаимодействие с фирмами-однодневками или «техническими компаниями» — это всегда риски при исполнении договоров и неприятные последствия при проверках налоговой.

  Функционал «Проверить аффилированность» поможет выявить связи между искомыми компаниями по учредителям и руководителям, построит все промежуточные связи по действующим и недействующим компаниям. Графическая визуализация связей делает простым и быстрым получение информации о всех промежуточных компаниях, а значит, вы легко сделаете выводы о благонадежности партнера.

  Для выявления аффилированности воспользуйтесь функцией «Проверить аффилированность». Введите в поиск необходимую компанию, с которой хотите построить связи. Сервис проверит по руководителям или совладельцам, какие типы связей и с кем были установлены.

  

  Для вашего спокойствия.
  Команда Seldon.Basis

  Источник

  Читайте также:  Шайба врезная для дерева