Определение ступени толщины дерева

Таксация леса

Таксационные показатели элементов леса и их определение, происхождение и структура древостоя. Определение среднего диаметра и высоты древостоя, его состав, оценка запасов и полноты. Класс товарности и форма насаждения. Изучение основных элементов леса.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

Размещено на http://www.allbest.ru/

Таксация леса как учебная дисциплина изучает методы всестороннего количественного и качественного учета и оценки древесины, как на корню, так и в заготовленном виде, закономерности строения, роста и прироста деревьев и древостоев. Для количественной и качественной характеристик объектов таксации необходимо знать их таксационные признаки (показатели): высоту, диаметр, площадь поперечного сечения, запас и т.д. Целью расчетно-графической работы является:

· закрепление теоретических знаний по определению основных таксационных показателей древостоя;

· приобретение навыков работы со справочной литературой.

Задачей расчетно-графической работы является определение основных таксационных показателей с использованием массовых таблиц и формул. Расчетное задание по определению основных таксационных показателей древостоя выполняется на основании материалов перечета деревьев и обмера высот на пробных площадях

В расчетно-графической работе необходимо описать или определить происхождение древостоя, элементы леса, средний диаметр, среднюю высоту, класс бонитета, класс возраста, полноту, запас, состав, класс товарности и форму насаждения.

Древостой-совокупность деревьев, иногда кустарников, являющихся основными компонентами насаждения.

Древостои могут быть представлены одним или двумя, иногда тремя ярусами главных и второстепенных пород. Таксационные показатели определяют по ярусам, а в пределах яруса — по элементам леса, они включают:

— Элементы леса (древесные породы);

— Средний диаметр древостоя;

— Класс бонитета насаждения;

— Класс товарности древостоя;

Таблица 1 — Данные сплошного пересчета деревьев на пробной площади

1. Происхождение древостоя

По происхождению древостой и насаждения бывают семенными и порослевыми, а также естественными и искусственными.

Насаждение представлено древостоем сосны и ели 80 лет — семенного происхождения.

Деревья в хвойных естественных насаждениях семенного происхождения имеют прямой ствол, различный возраст, расположены по площади неравномерно (хаотично), произрастают отдельными особями.

2. Элементы леса

В соответствии с действующей лесоустроительной инструкцией таксация насаждений производится по элементам леса.

Согласно учению Н.В. Третьякова «Элемент леса — последняя единица, до которой расчленяется лес». Элемент леса — чистое, однородное, одновозрастное насаждение или часть смешанного, сложного или разновозрастного, состоящее из деревьев одной породы, расположенных в одном ярусе, по возрасту относящихся к одному поколению и произрастающее в однородных лесорастительных условиях.

Насаждение включает столько элементов леса, сколько в нем пород, а по породам — сколько поколений. Различают основной элемент леса древостоя (преобладающую породу), который имеет наибольший запас, и второстепенные.

3. Средний диаметр древостоя

Каждый древостой состоит из тонких, средних и толстых деревьев. Толщиной дерева определяется размер и объем сортимента, который можно заготовить из него согласно ГОСТ 9462-88 «Лесоматериалы круглые лиственных пород», ГОСТ 3243-88 «Дрова» и ТУ-13-273685-404-89 «Дровяная древесина для технических нужд».

Для оценки среднего диаметра древостоя необходимо знать его изменчивость. Опытным путем установлено, что варьирование диаметров деревьев на высоте груди (1,3 м), в насаждении, зависит от возраста древостоя и составляет в искусственно созданных — 15-20%, одновозрастных естественных-20-30%, разновозрастных 30-40%.

Следовательно, наиболее точно средний диаметр можно определить по данным сплошного перечета в целом на участке или на его части, называемой пробной площадью. Перечет деревьев на пробе ведут по округленным диаметрам, называемым ступенью толщины. Интервал по ступеням зависит от среднего диаметра древостоя, который устанавливается примерно. При диаметре до 4,0 см используют 0,5 — сантиметровые ступени, при диаметре 4,1-8,0 — односантиметровые ступени, при диаметре 8,1 до 16,0 см — двухсантиметровые ступени; при диаметре 16,1 см и выше — четырехсантиметровые ступени.

Средний диаметр древостоя рассчитывают среднеарифметическим или среднеквадратическим способами.

Таблица 2 — Показатели для получения среднего диаметра сосны

Площадь сечения ступени g, м 2

Сумма площадей сечения по степеням толщины

Источник

10.2 Cтроение древостоев по диаметру

Распределение деревьев в древостое по диаметру является важнейшим элементом при изучении строения насаждений. Знание закономерностей распределение деревьев по толщине упрощает расчёт выхода сортиментов, особенно для чистых одновозрастных древостоев. Строение древостоев в целом характеризует лесоводственную структуру насаждения.

Первые закономерности распределения деревьев по диаметру установлены в конце Х1Х века. Австрийский ученый проф. В.Вейзе пришел к выводу, что число деревьев меньше среднего диаметра составляет в насаждении 57,5% от их общего числа, а больше — 42,5%.

Таким образом, среднее по толщине дерево делит все имеющиеся в древостое деревья на две неравные части. Закономерность, обнаруженная В. Вейзе, подтверждена позднейшими исследованиями, причем установлено, что она на­блюдается у всех древесных пород. Эта закономерность, определяющая место среднего дерева, имеет теоретическое и практическое значение, так как облегчает нахождение среднего диаметра.

Допустим, что в результате обмера в насаждении оказалось следующее распределение деревьев по ступеням толщины:

Ступени толщины, см . 12 16 20 24 28 32 36 40 44 48

Число деревьев 15 45 100 190 215 195 120 80 30 10 Итого 1000

В соответствии с найденной закономерностью 575 деревьев должны иметь диаметр меньше среднего, а остальные 425 деревьев – больше среднего. Следовательно, средний диаметр данной совокупности будет равен примерно 30 см.

Изучением закономерностей распределения деревьев в насаждениях по толщине занимался также венгерский проф. Л. Фекете. Он составил таблицу, в которой даны средние диаметры, кратные 5 см: 10, 15, 20, 25 см и т.д. Потом был найден диаметр самого тонкого дерева, далее — диаметр дерева, отграничивающего первые 10% более тонких деревьев, затем 20, 30% и т.д. через каждые 10%. Составив такую таблицу, Л. Фекете установил что, если в древостое заданного среднего диаметра отсчитать некоторое число деревьев, начиная с самого тонкого, выраженное в процентах от их общего числа, то у дерева, отграничивающего отсчитанный процент деревьев, диаметр будет определенной величиной.

Допустим, что насаждение имеет средний диаметр 25 см. Согласно таблице Л. Фекете диаметр самого тонкого дерева в древостое равен 13,8 см. Если в этом насаждении отобрать 10% самых тонких деревьев, то толщина последнего дерева, которое войдет в первые 10%, будет равна 17,3 см; если отобрать 20% более тонких деревьев, то дерево, отграничивающее эти 20%, будет иметь диаметр 19,3 см; если отсчитать 30% более тонких деревьев, то диаметр самого толстого дерева, входящего в эти 30%, будет равен 20,8 см и т.д. Такие вычисления были произведены Л. Фекете для древостоев разных средних диаметров. Диаметры деревьев указаны им в абсолютных числах (сантиметрах), отграниченных от самого тонкого дерева на величину, кратную 10%.

Более широко обобщил распределение деревьев в насаждениях по диаметру австрийский лесовод А. Шиффель, который выразил диаметры не в абсолютных числах, а в долях средних диаметров древостоев (R_D). Такие относительные значения диаметров в лесной таксации названы редукционными числами по диаметру. Таким образом, редукционное число по диаметру (R_D). есть частное от деления диаметра того или иного дерева на диаметр среднего дерева. Замена абсолютных значений диаметров относительными величинами позволяет в насаждениях разных средних диаметров сравнивать толщину деревьев, растущих в одинаковых условиях.

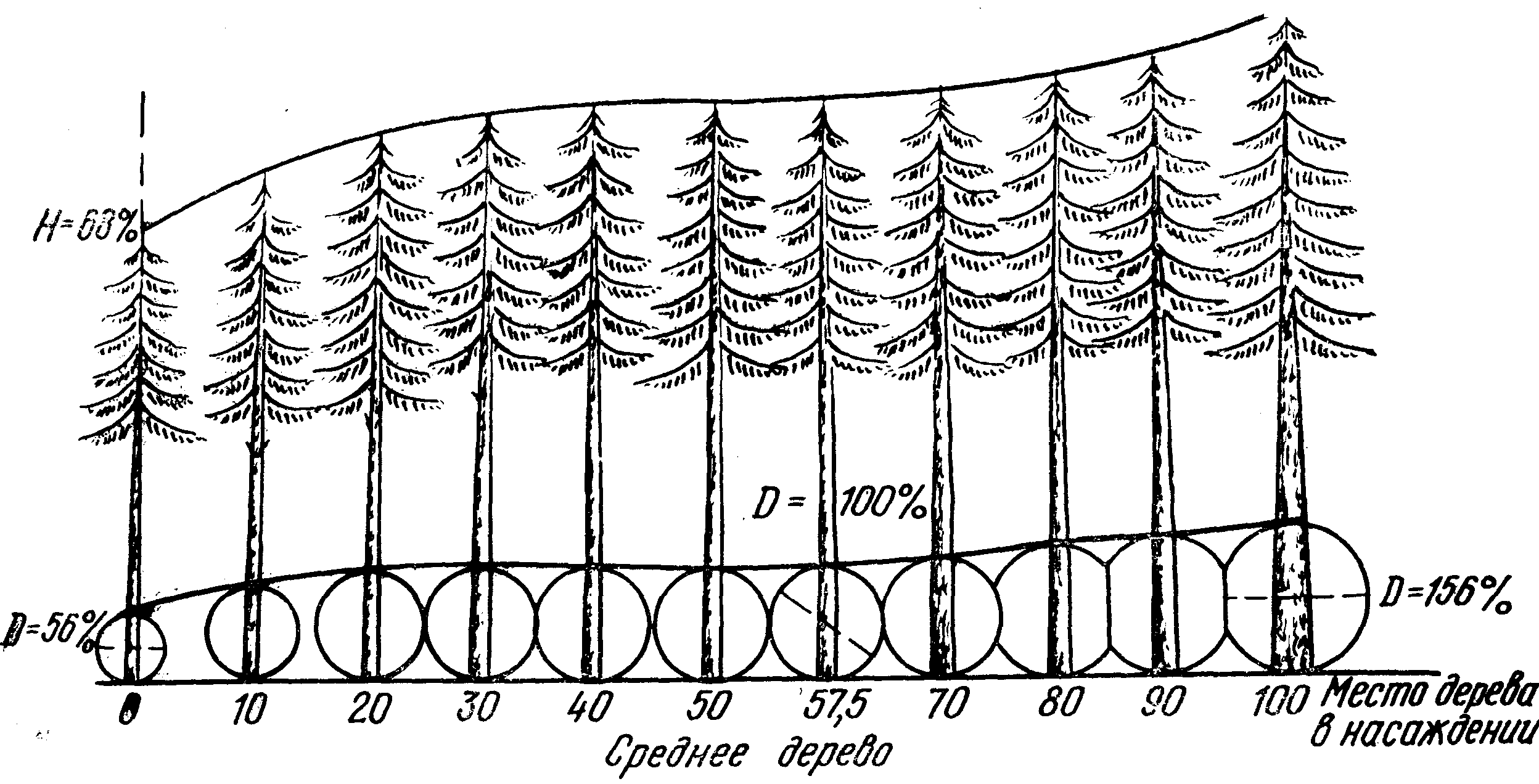
Все деревья, составляющие древостой, Шиффель распределил в последовательный ряд по возрастанию диаметров (рисунок 10.2). Этот ряд он разделил на десять частей. Для деревьев, оказавшихся на границе каждого из десяти отрезков, были найдены диаметры, выраженные в долях среднего диаметра, и в итоге составлена таблица редукционных чисел (таблица 10.1).

Из таблицы 10.1 видно, что диаметры деревьев, находящихся в древостое в одинаковых условиях, составляют определенную долю от среднего диаметра, иными словами, имеют одинаковые редукционные числа. Отклонения от этого правила наблюдаются лишь у насаждений со средним диаметром менее 20 см. Поэтому при выделении средних величин первые два ряда цифр не были приняты во внимание.

Из таблицы 10.2 видно, что диаметры деревьев, находящихся в древостое в одинаковых условиях, составляют определенную долю от среднего диаметра, иными словами, имеют одинаковые редукционные числа. Отклонения от этого правила наблюдаются лишь у насаждений со средним диаметром менее 20 см. Поэтому при выделении средних величин первые два ряда цифр не были приняты во внимание.

Наличие у древостоев общности в распределении деревьев по толщине, высоте и форме стволов принято называть закономерностями в строении насаждений.

Исследования Вейзе, Фекете и Шиффеля дали лишь первоначальные теоретические выводы по вопросу о строении древостоев. Современные ученые пришли к новым теоретическим обобщениям и разработали на основе закономерностей строения древостоев более совершенные методы учета древесных запасов и выхода сортиментов, широко используемые в современной таксационной практике

Рисунок 10.2. Схема распределения деревьев по размерам и их месту в насаждении (по А. Шиффелю)

А.В. Тюрин для выявления закономерностей в строении насаждении распределял деревья по ступеням толщины, выраженным в десятых долях среднего диаметра древостоя. Такие ступени, являющиеся общими для всех древостоев и не зависящим от конкретных диаметров, он назвал естественными ступенями толщины. В настоящее время их ещё называют относительными ступенями толщины.

Среднее распределение деревьев в процентах по естественным ступеням толщины было получено А.В. Тюриным в результате анализа многочисленных перечетов деревьев (таблица 10.2).

Замена ступеней, выраженных в сантиметрах, относительными значениями дала возможность сравнивать и выявлять общий характер перечетов деревьев в древостоях различных средних диаметров.. А.В. Тюрин пришел к выводу, что распределение деревьев по естественным ступеням толщины не зависит ни от породы, ни от бонитета, ни от полноты насаждений. В некоторой степени оно зависит от возраста древостоя, и в большой мере — от характера рубок ухода.

Таблица 10.1 Редукционные числа по диаметру для еловых насаждений (по А. Шиффелю)

Диаметры в долях среднего диаметра, отграниченные от низшей ступени на число процентов от общего числа деревьев

Источник