4.2. Ориентированные, упорядоченные и бинарные деревья
Ориентированным деревом (ордеревом, корневым деревом) называется орграф со следующими свойствами.
- Существует единственная вершина, полустепень захода которой равна 0. Она называется корнем ориентированного дерева.
- Полустепень захода всех остальных вершин равна 1.
- Каждая вершина достижима из корня.
а) все возможные ориентированные деревья с 3-я вершинами:
Концевая (висячая) вершина ордерева называется листом. Путь из корня в лист называется ветвью.
Уровень вершины ордерева – это расстояние от корня до вершины. Корень имеет уровень 0. Вершины одного уровня образуют ярус дерева.
Эквивалентное определение ориентированного дерева
Ордерево D – это конечное множество вершин, таких что:
1) имеется одна вершина r, называемая корнем данного дерева;
2) остальные вершины содержаться в k попарно непересекающихся множества D1,…Dk , каждое из которых является ордеревом. (k0) D= .
Множества D1,…,Dk называются поддеревьями.
Упорядоченным деревом называется ориентированное дерево, в котором:
- задан порядок поддеревьев
- каждое поддерево Di является упорядоченным поддеревом.
- дерево с одной вершиной считается упорядоченным поддеревом.
Замечание. При изображении ориентированных деревьев принято соглашение о том, что корень размещается вверху. В связи с этим все дуги оказываются ориентированными сверху вниз, поэтому стрелки на них можно не изображать. В результате, диаграммы свободных, ориентированных и упорядоченных деревьев оказываются графически неотличимыми. В этом случае требуется дополнительное указание, какого класса дерево изображено на диаграмме. Обычно это ясно из контекста.
Н апример: Имеются 3 диаграммы деревьев:
Как упорядоченные деревья, они все различны. Как ориентированные деревья D1=D2D3. Как свободные деревья, они все изоморфны D1=D2=D3.
Терема 3. Число упорядоченных деревьев с m дугами не превосходит 4 m .
Доказательство: Рассмотрим алгоритм обхода упорядоченного дерева, называемого «поиском в глубину». Этот обход рекурсивно описывается следующим образом:
- Начать с корня. Пока есть деревья выполнять.
- Перейти в корень очередного поддерева, обойти это поддерево в глубину.
- Вернуться в корень исходного поддерева.
В результате «обхода в глубину» по каждой дуге проходят ровно 2 раза: один раз при переходе в очередное поддерево, второй раз – при возвращении из него. В соответствии с «обходом в глубину» строиться последовательность из нулей и единиц. На каждом шаге записывается нуль, если происходит переход в очередное поддерево, а единица – при возвращении из поддерева. В результате получается последовательность из нулей и единиц длины 2m, которая называется кодом дерева. По этому коду однозначно восстанавливается дерево, т.к. каждый очередной разряд однозначно указывает, начинать ли строить новое очередное поддерево или возвращаться на ярус
ближе к корню. Таким образом. упорядоченных деревьев с m дугами не больше, чем последовательностей из нулей и единиц длины 2m. А их число равно 2 2 m =4 m . Теорема доказана.
Изоморфизм ориентированных деревьев определяется так же, как и изоморфизм графов, но с дополнительным условием — корень должен отображаться в корень. Для упорядоченных деревьев требуется также сохранение порядка поддеревьев.
Следствие. Число неизоморфных ориентированных или свободных деревьев с m ребрами не превосходит 4 m .
Доказательство: Выделив в неизоморфных свободных деревьях по одной вершине, мы получаем неизоморфные ориентированные деревья. Упорядочивая поддеревья в неизоморфных ориентированных поддеревьях, мы получаем упорядоченные деревья. Поэтому число неизоморфных свободных деревьев с m ребрами не превосходит числа неизоморфных ориентированных деревьев с m дугами, которое в свою очередь не превосходит числа неизоморфных (различных) упорядоченных деревьев с m дугами. Отсюда из теоремы 3 следует утверждение следствия.
Бинарное дерево – это конечное множество вершин, которое либо пусто, либо состоит из корня и не более двух непересекающихся бинарных поддеревьев – левого и правого. Заметим, что бинарное дерево не является упорядоченным.
Пример: два различных бинарных дерева:
Эти деревья изоморфны как упорядоченные, ориентированные и свободные, но не изоморфны как бинарные деревья.
Источник
9.2. Ориентированные, упорядоченные и бинарные деревья
Ориентированные (упорядоченные) деревья являются абстракцией иерархических отношений, которые очень часто встречаются как в практической жизни, так и в математике и в программировании. Дерево (ориентированное) и иерархия — это равнообъемные понятия.
9.2.1. Ориентированные деревья
Ориентированным деревом (или ордеревом, или корневым деревом) называется орграф со следующими свойствами:
- существует единственный узел r, полустепень захода которого равна 0, d + (r)=0. Он называется корнем ордерева.
- полустепень захода всех остальных узлов равна 1, vV \ d + (v)=1.
- каждый узел достижим из корня, vV \
.
Пример На рис. 9.5 приведены диаграммы всех различных ориентированных деревьев с 3 узлами, а на рис. 9.6 показаны диаграммы всех различных ориентированных деревьев с 4 узлами. 
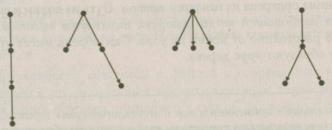
- q = p-l;
- если в ордереве отменить ориентацию ребер, то получится свободное дерево;
- в ордереве нет контуров;
- для каждого узла существует единственный путь, ведущий в этот узел из корня;
- подграф, определяемый множеством узлов, достижимых из узла v, является ордеревом с корнем v (это ордерево называется поддеревом узла v);
- если в свободном дереве любую вершину назначить корнем, то получится ордерево.
доказательство
- Каждая дуга входит в какой-то узел. Из п. 2 определения 9.2.1 имеем: vV-r d + (v)=1, где r – корень. Следовательно, q = p — l.
- Пусть G — ордерево, граф G’ получен из G забыванием ориентации ребер, r — корень. Тогда v1,v2V
G’&
, следовательно, v1,v2
и граф G’ связен. Таким образом, учитывая п. 4. теоремы 9.1.2, G’ — дерево.
- Следует из пункта 2.
- От противного. Если бы в G существовали два пути из u в v, то в G’ имелся бы цикл.
- Пусть Gv — правильный подграф, определяемый множеством узлов, достижимых из v. Тогда
, иначе узел v был бы достижим из какого-то узла v’ Gv и, таким образом, в Gv, а значит, и в G имелся бы контур, что противоречит пункту 3. Далее имеем: v’ Gv\ d + (v’) = 1, так как Gv G. Все вершины Gv достижимы из v по построению. По определению 9.2.1 получаем, что Gv -ордерево.
- Пусть вершина r назначена корнем и дуги последовательно ориентированы «от корня» обходом в глубину. Тогда d + (r) = 0 по построению; v V — r d + (v) = 1, так как входящая дуга появляется при первом посещении узла; все узлы достижимы из корня, так как обход в глубину посещает все вершины связного графа. Таким образом, по определению 9.2.1 получаем ордерево.
ЗАМЕЧАНИЕ Каждое свободное дерево определяет не более р ориентированных деревьев. Таким образом, общее число различных ордеревьев с р узлами не более чем в р раз превосходит общее число различных свободных деревьев с р вершинами. Концевая вершина ордерева называется листом. Путь из корня в лист называется ветвью. Длина наибольшей ветви ордерева называется высотой. Уровень узла ордерева — это расстояние от корня до узла. Сам корень имеет уровень 0. Узлы одного уровня образуют ярус дерева. ЗАМЕЧАНИЕ Наряду с «растительной» применяется еще и «генеалогическая» терминология. Узлы, достижимые из узла и, называются потомками узла и (потомки образуют поддерево). Если в дереве существует дуга (u, v), то узел и называется отцом (или родителем) узла v, a узел v называется сыном узла u. Сыновья одного узла называются братьями.
Источник
Ориентированные, упорядоченные и бинарные деревья.
Ориентированным деревом (ордеревом, корневым деревом) называется орграф со следующими свойствами.
- Существует единственная вершина, полустепень захода которой равна 0. Она называется корнем ориентированного дерева.
- Полустепень захода всех остальных вершин равна 1.
- Каждая вершина достижима из корня.
а ) все возможные ориентированные деревья с 3-я вершинами:
Концевая (висячая) вершина ордерева называется листом. Путь из корня в лист называется ветвью.
Уровень вершины ордерева – это расстояние от корня до вершины. Корень имеет уровень 0. Вершины одного уровня образуют ярус дерева.
Эквивалентное определение ориентированного дерева.
Ордерево D – это конечное множество вершин, таких что:
1) имеется одна вершина r, называемая корнем данного дерева;
2) остальные вершины содержаться в k попарно непересекающихся множествах D1,…Dk , каждое из которых является ордеревом. (k0) D= .
Множества D1,…,Dk называются поддеревьями.
Упорядоченным деревом называется ориентированное дерево, в котором:
- задан порядок поддеревьев
- каждое поддерево Di является упорядоченным поддеревом.
- дерево с одной вершиной считается упорядоченным поддеревом.
Замечание. При изображении ориентированных деревьев принято соглашение о том, что корень размещается вверху. В связи с этим все дуги оказываются ориентированными сверху вниз, поэтому стрелки на них можно не изображать. В результате, диаграммы свободных, ориентированных и упорядоченных деревьев оказываются графически неотличимыми. В этом случае требуется дополнительное указание, какого класса дерево изображено на диаграмме. Обычно это ясно из контекста.
Н апример: Имеются 3 диаграммы деревьев:
Как упорядоченные деревья, они все различны. Как ориентированные деревья D1=D2D3. Как свободные деревья, они все изоморфны D1=D2=D3.
Терема 3. Число упорядоченных деревьев с m дугами не превосходит 4 m .
Доказательство: Рассмотрим алгоритм обхода упорядоченного дерева, называемого «поиском в глубину». Этот обход рекурсивно описывается следующим образом:
- Начать с корня. Пока есть деревья выполнять.
- Перейти в корень очередного поддерева, обойти это поддерево в глубину.
- Вернуться в корень исходного поддерева.
В результате «обхода в глубину» по каждой дуге проходят ровно 2 раза: один раз при переходе в очередное поддерево, второй раз – при возвращении из него. В соответствии с «обходом в глубину» строиться последовательность из нулей и единиц. На каждом шаге записывается нуль, если происходит переход в очередное поддерево, а единица – при возвращении из поддерева. В результате получается последовательность из нулей и единиц длины 2m, которая называется кодом дерева. По этому коду однозначно восстанавливается дерево, т.к. каждый очередной разряд однозначно указывает, начинать ли строить новое очередное поддерево или возвращаться на ярус ближе к корню. Таким образом, упорядоченных деревьев с m дугами не больше, чем последовательностей из нулей и единиц длины 2m. А их число равно 2 2 m =4 m . Теорема доказана.
Изоморфизм ориентированных деревьев определяется так же, как и изоморфизм графов, но с дополнительным условием — корень должен отображаться в корень. Для упорядоченных деревьев требуется также сохранение порядка поддеревьев.
Следствие. Число неизоморфных ориентированных или свободных деревьев с m ребрами не превосходит 4 m .
Доказательство: Выделив в неизоморфных свободных деревьях по одной вершине, мы получаем неизоморфные ориентированные деревья. Упорядочивая поддеревья в неизоморфных ориентированных поддеревьях, мы получаем упорядоченные деревья. Поэтому число неизоморфных свободных деревьев с m ребрами не превосходит числа неизоморфных ориентированных деревьев с m дугами, которое в свою очередь не превосходит числа неизоморфных (различных) упорядоченных деревьев с m дугами. Отсюда из теоремы 3 следует утверждение следствия.
Бинарное дерево – это конечное множество вершин, которое либо пусто, либо состоит из корня и не более двух непересекающихся бинарных поддеревьев – левого и правого. Заметим, что бинарное дерево не является упорядоченным.
П ример: На рисунке представлены два различных бинарных дерева:
То есть, эти деревья изоморфны как упорядоченные, ориентированные и свободные, но не изоморфны как бинарные деревья.
Источник
 .
. G’&
G’& , следовательно, v1,v2
, следовательно, v1,v2 и граф G’ связен. Таким образом, учитывая п. 4. теоремы 9.1.2, G’ — дерево.
и граф G’ связен. Таким образом, учитывая п. 4. теоремы 9.1.2, G’ — дерево.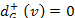 , иначе узел v был бы достижим из какого-то узла v’ Gv и, таким образом, в Gv, а значит, и в G имелся бы контур, что противоречит пункту 3. Далее имеем: v’ Gv\ d + (v’) = 1, так как Gv G. Все вершины Gv достижимы из v по построению. По определению 9.2.1 получаем, что Gv -ордерево.
, иначе узел v был бы достижим из какого-то узла v’ Gv и, таким образом, в Gv, а значит, и в G имелся бы контур, что противоречит пункту 3. Далее имеем: v’ Gv\ d + (v’) = 1, так как Gv G. Все вершины Gv достижимы из v по построению. По определению 9.2.1 получаем, что Gv -ордерево.