1. Создание дерева решений
создает дерево решений t как функцию, предсказывающую ответ y в зависимости от набора независимых переменных X. X – n-на-m матрица — обучающая выборка. Если y вектор из n значений, то функция строит дерево регрессии, если же y – категориальная переменная, то строится дерево классификации. В любом случае t представляет собой бинарное дерево, в котором каждый узел ветвления основан на значениях из столбца матрицы X.
t = classregtree(X,y,’Name‘,value)
задает один или более пар параметров name/value. Name задается в кавычках. Доступны следующие опции:
- categorical — вектор индексов столбцов матрицы X, которые являются категориальными переменными;
- prune — ‘on’ (по умолчанию) вычислить полное дерево и оптимальную последовательность сокращенных поддеревьев, или ‘off’ для полного дерева без сокращения;
- minparent —число k такое, что узел должен иметь k или более наблюдений, чтобы расщепляться (по умолчанию 10);
- minleaf — минимальное число наблюдений для листа дерева (по умолчанию 1).
Только для деревьев классификации:
- cost — квадратная матрица C, где C(i,j) стоимость неправильной классификации точка класса j помещенной в класс i (по умолчанию C(i,j)=1 если i~=j, и C(i,j)=0 если i=j).
- splitcriterion — критерий для выбора расщепления. По умолчанию ‘gdi’ Gini индекс;
Пример использования функции.
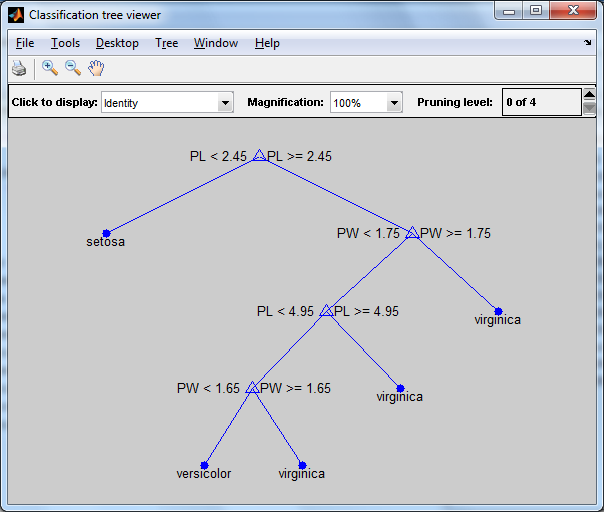
Создадим дерево классификации для ирисов Фишера. Функция выводит правила принятия решений. Чтобы нарисовать диаграмму правил принятия решений и определения классов, воспользуемся функцией view(t).
t = Decision tree for classification
1 if PL=2.45 then node 3 else setosa
3 if PW=1.75 then node 5 else versicolor
4 if PL=4.95 then node 7 else versicolor
6 if PW=1.65 then node 9 else versicolor
Рисунок 2.5 – Диаграмма правил принятия решений и определения классов для классификации ирисов Фишера по 4 параметрам
2. Прогнозирование с использованием полученного дерева решений.
yfit = eval(t,X) используя дерево классификации t и матрицу X независимых переменных вычисляет вектор yfit прогнозируемых значений классов.
3. Сокращение дерева.
t2 = prune(t1,’level’,level) берет дерево решений t1 уровень сокращения level, и возвращает дерево решений t2, сокращенное до указанного уровня. Если level = 0, сокращение не производится.
4. Тестирование качества классификации
использует тестовую выборку X и y , применяет дерево решений t к этому набору примеров, и возвращает вектор cost количества или стоимости ошибок, вычисленных для тестового примера.
использует 10-шаговую кросс-валидацию для вычисления вектора cost. X и y должны быть обучающей выборкой, то есть примером, который использовался для построения дерева t. Функция делит пример на 10 подмножеств, выбранных случайным образом, ноприблизительно равного размера с сохранением пропорций классов обучающей выборки. Для каждого подмножества test создает дерево для оставшихся данных и использует его для предсказания классов подмножества. Затем объединяет информацию по всем подмножествам, чтобы оценить ошибку cost для всей выборки.
Пример 2.3. Выполним классификацию ирисов Фишера по двум параметрам с помощью построения дерева решений. Создадим дерево решений и посмотрим насколько хорошо работает этот метод.
t = classregtree(meas(:,1:2), species,’names’,…
Посмотрим как дерево решений разделяет плоскость.
Рисунок 2.6 – Разделение плоскости значений параметров классификации деревом решений
Другой путь увидеть дерево решений – нарисовать диаграмму правил принятия решений и определения классов.
Рисунок 2.7 – Дерево решений для задачи классификации ирисов Фишера по двум параметрам
Вычислим ошибку на обучающем множестве и ошибку кросс-валидации для дерева решений.
dtClassFun = @(xtrain,ytrain,xtest) (eval(classregtree(xtrain,ytrain),xtest));
Для построенного дерева решений ошибка кросс валидации оказалась значительно больше, чем ошибка на обучающем множестве. Это свидетельствует о переобучении. Другими словами, это дерево, которое классифицирует обучающее множество хорошо, но структура дерева чувствительна к обучающей выборке так что классификация на новых данных работает заметно хуже. Часто возможно построить более простое дерево, которое будет работать лучше.
Попробуем сократить дерево. Прежде всего вычислим ошибку классификации на обучающем (resubstitution) множестве для различных подмножеств исходного дерева. Затем вычислим ошибку кросс-валидации на поддеревьях. График показывает, что ошибка на обучающем множестве достаточно оптимистическая. Она всегда уменьшается с ростом дерева, однако, начиная с некоторой точки, ошибка кросс-валидации растет с ростом узлов дерева.
xlabel(‘Number of terminal nodes’);
ylabel(‘Cost (misclassification error)’)
Очевидно, что следует выбрать дерево, которое дает минимальную ошибку кросс-валидации и приемлемую ошибку на обучающем множестве. Для этого примера выбираем простейшее дерево, которое дает минимальную ошибку. Это правило используется по умолчанию classregtree/test методом.
Это можно показать на графике, вычисляя величину cutoff, которая равна минимальной стоимости+1 ошибки. «Лучший» уровень, вычисляемый методом classregtree/test , это минимальное дерево для заданного порога отсечения cutoff. (Заметим, что bestlevel=0 соответствует несокращенному дереву, поэтому добавляем 1, чтобы использовать значение как индекс в выходном векторе classregtree/test.
Рисунок 2.8 — Ошибки классификации в зависимости от размера дерева решений
cutoff = mincost + secost(minloc);
plot(ntermnodes(bestlevel+1), cost(bestlevel+1), ‘mo’)
legend(‘Cross-validation’,’Resubstitution’,’Min + 1 std. err.’,’Best choice’)
Наконец, посмотрим на сокращенное дерево и вычислим ошибку классификации.
Рисунок 2.9 – Выбор оптимального количества узлов
Рисунок 2.10 – Сокращенное дерево решений
Источник