Основные операции над бинарными деревьями

Операции над бинарным деревом

Над бинарным деревом могут быть выполнены операции:

• обход узлов бинарного дерева в определенном порядке;
• добавление некоторого поддерева в дерево;
• исключение некоторого поддерева из дерева;
• примитивные операции над узлами дерева.

Обход (прохождение) дереваиспользуется для систематического последовательного просмотра узлов дерева. Эта операция может быть использована для контроля информации, хранящейся в древовидной структуре, а также как составная часть для выполнения других операций над деревом. Рекурсивная процедура обхода дерева включает в себя следующие шаги: 1) обработка (просмотр) корня дерева или поддерева; 2) обход левого поддерева обработанного корня; 3) обход правого поддерева обработанного корня; Различный порядок выполнения перечисленных выше шагов определяет три процедуры обхода бинарного дерева: 1) обход сверху вниз– сначала обрабатывается корень, затем обходится его левое, затем правое поддеревья (операцияUpDownRevision); 2) обход слева направо– сначала обходится левое поддерево корня, затем обрабатывается корень, затем обходится его правое поддерево (операцияLeftRightRevision); 3) обход снизу вверх– обходится левое поддерево корня, затем правое, затем обрабатывается корень (операцияDownUpRevision). При обходе каждого из приведённых ниже бинарных деревьев получим по три упорядоченные последовательности: (а)(б)обходдерево (а)дерево (б) сверху вниз ABDEGCFHI+a/bc–def(префиксная запись) слева направо DBGEACHFIa+b/cd–ef(инфиксная без скобок) снизу вверх DGEBHIFCAabc/+def–(постфиксная запись) Добавление некоторого поддерева в дерево. Для выполнения этой операции должны быть заданы: включаемое поддерево и узел исходного дерева, к которому поддерево подключается в качестве ветви. Поскольку бинарное дерево является упорядоченным, то должно быть указание на то, в качестве какой ветви (левой или правой) заданного узла должно быть подключено поддерево. Целесообразно разбить эту операцию на две: включение поддерева в качестве левой ветви заданного узла (AddLeft) и включение в качестве правой ветви заданного узла (AddRight). Ветви, в которые осуществляется включение, должны быть пустыми. Исключение некоторого поддерева из деревафактически представляет собой две операции: исключение поддерева из левой ветви заданного узла исходного дерева (DeleteLeft) и исключение поддерева из его правой ветви (DeleteRight). Операция возвращает адрес исключенного поддерева. Примитивные операциинад узлами бинарного дерева могут быть следующими.Addr(v) возвращает адрес узла со значениемv. Еслиp– указатель на узелNodeбинарного дерева, то операцияValue(p)возвращает значение узлаNode. ОперацииLeft(p),Right(p),Father(p),Brother(p)возвращают соответственно указатели на левого сына, правого сына, отца и брата узлаNode. ОперацииIsLeft(p)иIsRight(p)возвращают значение «истина», еслиNodeявляется соответственно левым илиправым сыном некоторого узла дерева, и значение «ложь» – в противном случае. Дополнительно могут быть определены следующие операции: Create– создание пустого дерева,Clear– удаление всех узлов дерева,WriteTo(f) – вывод дерева в файлfс помощью отступов,NodesQuantity– определение числа узлов дерева.

Для продолжения скачивания необходимо пройти капчу:

Источник

4.10.Структуры данных типа дерева. Основные операции над бинарными деревьями. Решение задачи сортировки с помощью дерева. Примеры программирования операций над деревьями.

Дерево – это структура, содержащая узел T, с которым связано конечное число древовидных структур с базовым типом T, называемых поддеревьями.

Верхний узел дерева – это корень. Каждый новый узел – это новый уровень дерева и, соответственно, потомок предыдущего узла. Если узел не имеет потомков – он называется листом (терминальный узел).

Элемент, не являющийся терминальным – внутренний узел. Путь к следующему уровню – ребро дерева (ветвь). Число “ветвей” определяет длину пути к определенному узлу.

Бинарное дерево – дерево, каждый узел которого соединен не более чем с 2мя поддеревьями.

Для построения идеально сбалансированного дерева минимальной высоты нужно располагать максимально возможное число узлов на всех уровнях, кроме самого нижнего. Алгоритмически это реализуется распределением узлов поровну справа или слева от каждого узла.

Рекурсивная процедура, реализующая такую последовательность построения, должна состоять из следующих действий:

1. Выбрать один узел в качестве корня

2. Построить левое поддерево 

3. Построить правое поддерево 

begin date:=x; left:=nil; rigth:=nil; end; Root:=p;

Если узел является терминальным, тогда поле ссылки равно null.

Основные операции над деревом:

1.Поиск элемента. 2.Удаление элемента. 3.Вставка элемента.

4.Упорядочить деревья по заданному признаку (не только сортировка).

Cбалансированное дерево. Сбалансированным считается дерево, если на каждом его уровне располагается максимально возможное число узлов.

1 . Поиск – это движение по дереву

Function Poisk(var t:node;r:integer):boolean;

while (p<> nil) and not flag do

if r = p^.date then flag:=true  найден искомый элемент

else if r > p^.date then p: = p^.left

else p: = p^.right ;  движение по узлам дерева

end;

2. Удаление элементов созданного дерева.

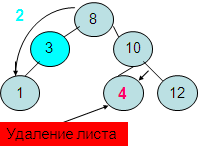
2.1. Удаление листа – удаляется ссылка на лист из соответствующего поддерева

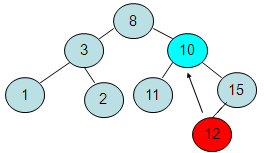
2 .2. Удаление узла с одной ссылкой – ссылку верхнего узла надо заменить на удаляемую ссылку

2.3. Удаляемый узел содержит две ссылки – удаляемый узел замещается самым правым узлом левого поддерева или самым левым узлом правого поддерева

If r^. right =nil then begin

q^. date:=r^. date; — запоминаем значение

qk :=r; — сохраняем найденный узел

r :=r^. Left; Dispose(qk); end else

Бинарное дерево поиска можно использовать для сортировки. Для этого берётся пустое дерево, к нему добавляют все элементы массива, а затем, используя алгоритм «Обход дерева», записывают элементы дерева в массив в возрастающем порядке.

public Tree left,right; // левое и правое поддеревья и ключ

/* insert (добавление нового поддерева (ключа)). сравнить ключ добавляемого поддерева (К) с ключом корневого узла (X).

public void insert( Tree aTree)

if ( right != null ) right.insert( aTree );

Рекурсивно обойти левое поддерево. Применить функцию f (печать) к корневому узлу. Рекурсивно обойти правое поддерево. */

public void traverse(TreeVisitor visitor)

if ( right != null ) right.traverse( visitor ); > >

public void visit(Tree node);>

class KeyPrinter implements TreeVisitor

public static void main(String args[])

myTree = new Tree( 7 ); // создать дерево (с ключом)

myTree.insert( new Tree( 5 ) ); // присоединять поддеревья

myTree.insert( new Tree( 9 ) ); myTree.traverse(new KeyPrinter());>

void preorder(CTreeNode* ctree, int k)

if (ctree->right != null) preorder(ctree->right,k+1);>

Источник