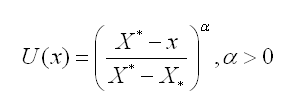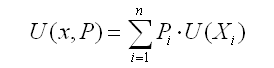Оценка рисков дерево решений пример

Дерево решений

Для построения дерева решений не существует универсального набора символов, но чаще всего квадраты (□) используются для представления «решений», а круги (○) для представления «результатов». Поэтому я буду использовать в своей статье именно эти символы.

Дерево решений и задача, требующая многошагового принятия решений

Дерево решений – это представление задачи в виде диаграммы, отражающей варианты действий, которые могут быть предприняты в каждой конкретной ситуации, а также возможные исходы (результаты) каждого действия. Такой подход особенно полезен, когда необходимо принять ряд последовательных решений и (или) когда на каждом этапе процесса принятия решения могут возникать множественные исходы.
Например, если рассматривается вопрос, стоит ли расширять бизнес, решение может зависеть более чем от одной переменной.

Например, может существовать неопределенность как в отношении объема продаж, так и величины затрат. Более того, значение некоторых переменных может зависеть от значения других переменных: например, если будет продано 100,000 единиц продукта, себестоимость единицы продукта составит $4, но если будет продано 120,000 единиц, себестоимость единицы снизится до $3.80. Таким образом, возможны различные исходы ситуации, при этом некоторые из них будут зависеть от предыдущих исходов. Дерево решений представляет собой полезный метод разделения сложной задачи на более мелкие и более управляемые подзадачи.

Решение задачи при помощи дерева решений осуществляется в два этапа. Первый этап включает построение дерева решений с указанием всех возможных исходов (финансовых результатов) и их вероятностей. Следует помнить, что при принятии решений нужно опираться на принцип релевантных затрат, т. е. использовать только релевантные затраты и выручку. Второй этап включает оценку и формулировку рекомендаций. Принятие решения осуществляется путем последовательного расчета ожидаемых значений исходов в обратном порядке  от конца к началу (справа налево). После этого формируются рекомендации для руководства по выбору оптимального образа действий.

Построение дерева решений

Дерево решений всегда следует строить слева направо. Выше я упоминал «решения» и «исходы». Точки принятия решений представляют собой варианты альтернативных действий, то есть возможные выборы. Вы принимаете решение пойти либо этим, либо другим путем. Исходы (результаты решений) от вас не зависят. Они зависят от внешней среды, например, от клиентов, поставщиков или состояния экономики в целом. Как из точек принятия решений, так и из точек исходов выходят «ветви» дерева. Если существует, например, два возможный варианта действий, из точки принятия решения будут выходить две ветви, и если существует два возможных исхода (например, хороший и плохой), то из точки исхода тоже будут выходить две ветви. Поскольку дерево решений является инструментом оценки различных вариантов действий, то все деревья решений должны начинаться с точки принятия решения, которая графически представляется квадратом.

Пример простого дерева решений показан ниже. Из рисунка видно, что лицо, принимающее решение, может выбрать из двух вариантов, поскольку из точки

принятия решения выходит две ветви. Исход одного из вариантов действий, представленного верхней ветвью, точно известен, поскольку на этой ветви нет никаких точек возможных исходов. Но на нижней ветви есть круг, который показывает, что в результате данного решения возможны два исхода, поэтому из него исходят две ветви. На каждой из этих двух ветвей тоже имеется по кругу, из которых, в свою очередь, тоже выходят по две ветви. Это значит, что для каждого из упомянутых возможных исходов имеется два варианта развития ситуации, и каждый из вариантов имеет свой исход. Возможно, первые два исхода представляют собой различные уровни дохода в случае осуществления определенной инвестиции, а второй ряд исходов — различные варианты переменных затрат для каждого уровня доходов.

После построения основы дерева, как показано выше, необходимо указать финансовые значения исходов и их вероятности. Важно помнить, что вероятности, указанные для ветвей, исходящих из одной точки, в сумме должны давать 100%, иначе это будет означать, что вы не указали на диаграмме какой-либо результат, или допустили ошибку в расчетах. Пример приведен ниже в статье.

После построение дерева решений необходимо оценить решение.

Оценка решения

Дерево решений оценивается справа налево, т. е. в направлении, обратном тому, которое использовалось для построения дерева решений. Для того, чтобы осуществить оценку, вы должны предпринять следующие шаги:

1. Подпишите все точки принятия решений и исходов, т.е. все квадраты и круги. Начните с тех, которые расположены в самой правой части диаграммы, сверху вниз, и затем перемещайтесь влево до самого левого края диаграммы.
2. Последовательно рассчитайте ожидаемые значения всех исходов, двигаясь справа налево, используя финансовые показатели исходов и их вероятности.

Наконец, выберите вариант, который обеспечивает максимальное ожидаемое значение исхода и подготовьте рекомендации для руководства.

Важно помнить, что использование ожидаемых значений для принятия решения имеет свои недостатки. Ожидаемое значение – это средневзвешенное значение исходов решения в долгосрочной перспективе, если бы это решение принималось много раз.
Таким образом, если мы принимаем однократное решение, то фактический результат

быть далек от ожидаемого значения, поэтому данный метод нельзя назвать очень точным. Кроме того, рассчитать точные вероятности довольно сложно, поскольку конкретная рассматриваемая ситуация могла никогда не случаться в прошлом.

Метод ожидаемого значения при принятии решений полезен тогда, когда инвестор имеет нейтральное отношение к риску. Такой инвестор не принимает на себя чрезмерные риски, но и не избегает их. Если отношение к риску лица, принимающего решение, неизвестно, то сложно сказать, стоит ли использовать метод ожидаемого значения. Может оказаться более полезным просто рассмотреть наихудший и наилучший сценарии, чтобы создать основу для принятия решения.

Я приведу простой пример использования дерева решений. В целях упрощения считайте, что все цифры являются чистой приведенной стоимостью соответствующего показателя.

Пример 1
Компания принимает решение, стоит ли разрабатывать и запускать новый продукт. Ожидается, что затраты на разработку составят $400,000, при этом вероятность того, продукт окажется успешным, составляет 70%, а вероятность неудачи, соответственно, 30%. Ниже приведена оценка прибыли от продажи продукта, в зависимости от уровня спроса – высокого, среднего или низкого, а также соответствующие каждому уровню вероятности:

Источник

3. Оценка риска с применением теории полезности. Построение дерева решений. Функции полезности. Измерение отношения к риску. Пример. Оценка риска с применением теории полезности.

Существует несомненная связь между хозяйственным риском конкретных предприятий и личностными характеристиками лиц из числа руководства и специалистов предприятия, принимающих решения. Кроме того, успех в деятельности конкретного предприятия, представляющего на рынок определенные товары или услуги, в значительной степени зависит от правильности учета психологических особенностей потребителей, их отношения к риску — рисковать, или всячески страховать себя от возможных финансовых потерь, например, при покупке новых неизвестных товаров или услуг. Поэтому целесообразно рассмотреть различия в отношении людей к риску, хотя бы в финансовом отношении.

Для принятия оптимальных решений в условиях неопределенности и вызванного его риска с учетом отношения людей к риску используют элементы теории полезности.

Полезность отражает степень удовлетворения конкретного субъекта определенным товаром (изделием или услугой), а также действием. Использование полезности позволяет соизмерять вещи, которые физически являются несоизмеримыми, ее часто используют для ранжирования приоритетов при выборе.

Используя различные функции полезности, можно описать процедуры оценки конкретных экономических ситуаций через нахождение ожидаемого значения функции.

1. Из всего множества Х, предложенных экспертом значений определенного экономического показателя выделяют два значения X_* и X*, таким образом, что X ≥ X* (означает, что Х не хуже, чем X*, однако эксперт не делает между ними особой разницы) и X ≤ X* (означает, что X* не хуже, чем X, но эксперт не делает между ними особой разницы) для всех х ∈ Х. Таким образом получают два крайних значения шкалы X_* и X*.

2. Эксперту предлагают сравнить между собой два показателя: Xi и лотерею — получить X_* с вероятностью Р или X* с вероятностью (1-Р). Меняя величину Р, добиваются того, что значения Xi и лотерея L (X_*, X*, Р) станут, по мнению эксперта эквивалентными.

Фиксируют значение Xi и Рi для этой ситуации. Процесс повторяют меняя X i в интервале от X_* до X*.

3. Минимальному и максимальному значениям X_* и X* присваивают произвольные числовые значения полезности Umin=U(X_*) и Umax=U(X*), при этом соблюдают, чтобы Umax> Umin.

4. Полезность варианта определяется вероятностью U(x)=P(x), при которой человеку безразлично, что выбирать: гарантированный вариант или лотерею, см. выше п.2.

Например, в качестве функций полезности можно брать:

или

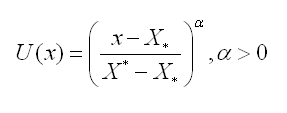
Первая, является растущей, вторая — убывающей.

Ожидаемое значение полезности ряда альтернативных результатов рассчитывается как средневзвешенное их полезностей по вероятностям.

Построение дерева решений.

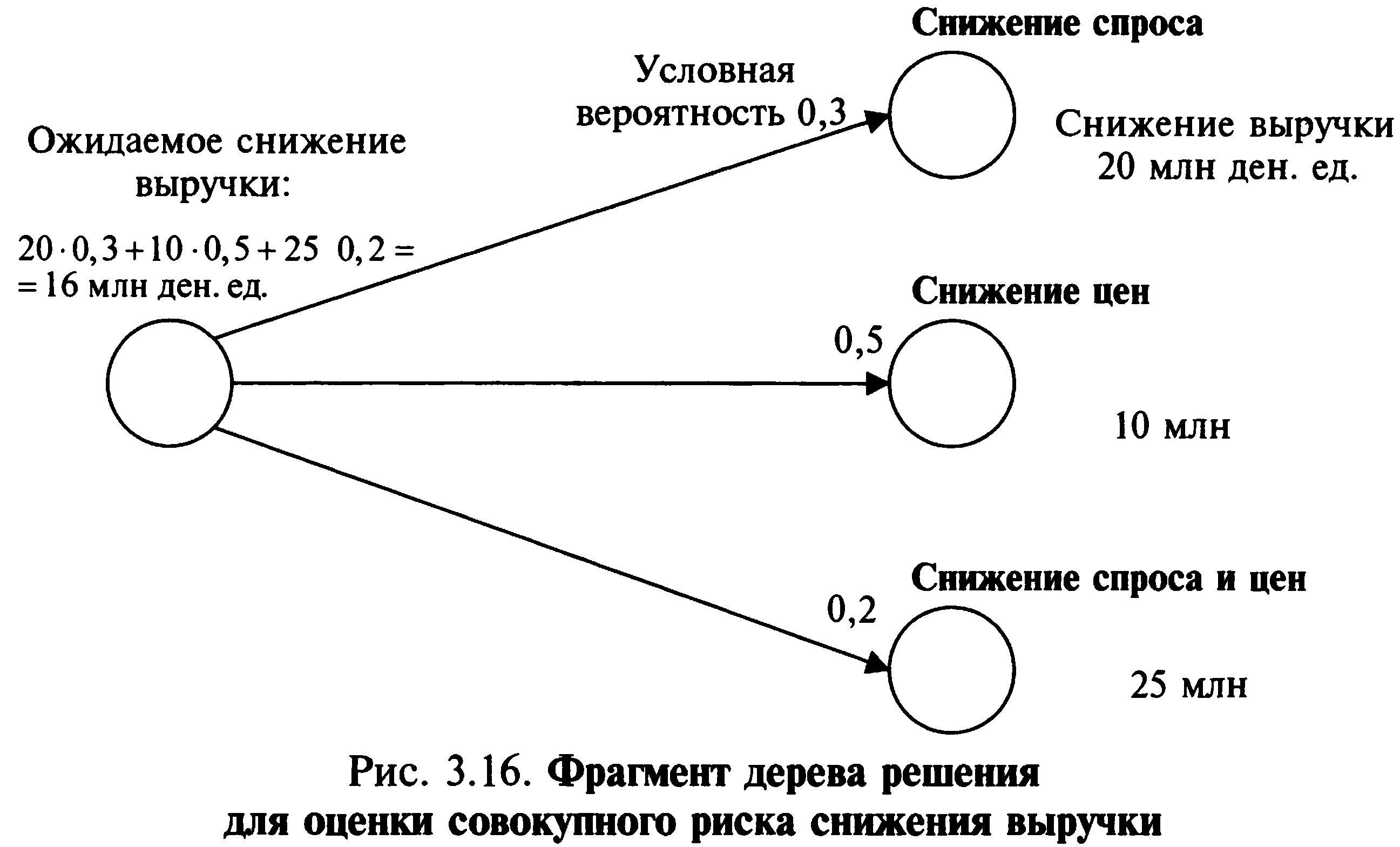
К важным инструментам исследования риска относится моделирование задачи выбора с помощью построения сложных распределений вероятностей (деревьев решений) — графического (сетевого) построения вариантов возможных решений. По ветвям дерева соотносят субъективные и объективные оценки возможных событий. Следуя вдоль построенных ветвей и используя специальные методики расчета вероятностей, оценивают каждый путь и выбирают менее рискованный. Последствия возникновения ситуации рассчитываются как произведение условной вероятности на оценку последствий. Пример построения дерева решений и оценка рисков на его основе представлены на рис. 3.16. Для непосредственного построения дерева решений часто используется метод сценариев («что, если. »). Дерево решений позволяет в графической форме изобразить причинно-следственную зависимость между рисковыми ситуациями и их последствиями, а затем по каждой группе альтернативных (взаимоисключающих и при этом одновременно возможных) событий определить условные вероятности и меры риска, что позволяет рассчитать усредненную оценку рисков. Таким образом формируется сценарий развития рисковых ситуаций (рис. 3.16).

Дерево решений позволяет провести анализ риска лишь в статике, что ограничивает применение этого метода.

Источник