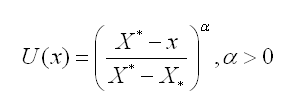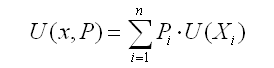Оценка рисков дерево решений примеры

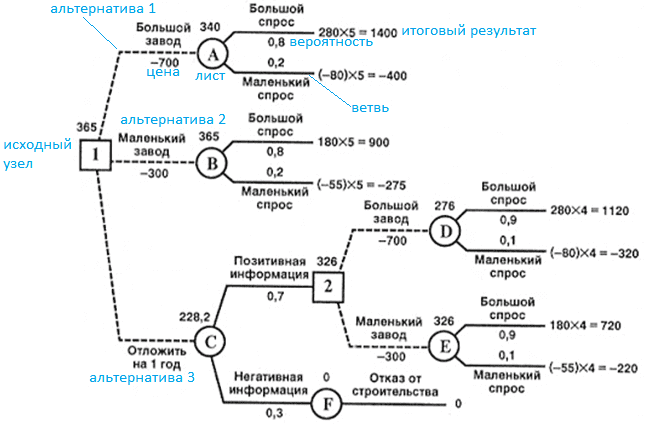
8.10. Метод «дерево решений»

Для анализа рисков инновационных проектов часто применяют метод дерева решений. Он предполагает, что у проекта существует несколько вариантов развития. Каждое решение, принимаемое по проекту, определяет один из сценариев его дальнейшего развития. При помощи дерева решений решаются задачи классификации и прогнозирования. Дерево решений – это схематическое представление проблемы принятия решений. Ветви дерева решений представляют собой различные события (решения), а его вершины – ключевые состояния, в которых возникает необходимость выбора. Чаще всего дерево решений является нисходящим, т. е. строится сверху вниз. Выделяют следующие этапы построения дерева решений:

1. Первоначально обозначают ключевую проблему. Это будет вершина дерева.
2. Для каждого момента определяют все возможные варианты дальнейших событий, которые могут оказать влияние на ключевую проблему. Это будут исходящие от вершины дуги дерева.
3. Обозначают время наступления событий.
4. Каждой дуге прописывают денежную и вероятностную характеристики.
5. Проводят анализ полученных результатов.

Основа наиболее простой структуры дерева решений – ответы на вопросы «да» и «нет». Пример 1. Рассмотрим пример дерева решений, задача которого – ответить на вопрос «Пойти ли гулять?». Чтобы решить эту задачу, необходимо ответить на ряд вопросов, которые находятся в узлах дерева (рис. 8.1). Вершина дерева «На улице солнечно» является узлом проверки. Если на этот вопрос получен положительный ответ, то переходим к левой ветви дерева, если отрицательный – то к правой. Движение продолжается до тех пор, пока не будет получен окончательный ответ. 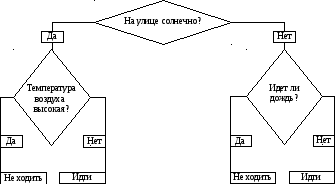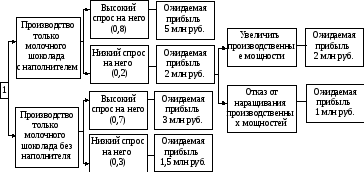Рис. 8.1. Дерево решений «пойти ли гулять» Для каждой дуги дерева могут быть определены числовые характеристики, например величина прибыли по проекту и вероятность ее получения. В этом случае оно помогает учесть все возможные варианты действия и соотнести с ними финансовые результаты. Для формулирования сценариев развития проекта необходимо располагать достоверной информацией с учетом вероятности и времени наступления событий. Затем переходят к сравнению альтернатив. Пример 2. Компания «Конфетти» в настоящее время выпускает плитки молочного шоколада. Директор по развитию считает, что на рынке повысился спрос на молочный шоколад с наполнителями. Перед компанией стоит вопрос: переходить ли на производство молочного шоколада с наполнителем или не стоит этого делать? Если производить шоколад обоих типов, то потребуется увеличить производственные мощности. Информация об ожидаемых выигрышах и вероятности событий в случае того или иного решения представлена на дереве решений (рис. 8.2). Используя дерево решений, руководитель находит наиболее предпочтительное решение – увеличить производственные мощности. Это обусловлено ожидаемой прибылью – 2 млн руб., которая превышает прибыль 1 млн руб. при отказе от такого наращивания, если в точке «а» будет низкий спрос. Руководитель, двигаясь к первой точке принятия решения, рассчитывает предполагаемую прибыль в случае альтернативных действий. Рис. 8.2. Дерево решений «какой шоколад производить» Для производства только молочного шоколада с наполнителем она составит 4,4 млн руб. (5 × 0,8 + 0,2 × 2). Аналогично рассчитывается ожидаемое значение для варианта выпуска только молочного шоколада без наполнителя, которое равно всего 2,55. Таким образом, наращивание производственных мощностей является наиболее желательным решением и приносит наибольший выигрыш. Пример 3. Руководителю отдела нужно принять решение относительно закупки станков. Второй станок более экономичный, но и в то же время более дорогой и требует больших накладных расходов (рис. 8.3). Руководителю нужно выбрать тот станок, который обеспечит максимизацию прибыли.

Оборудование	Постоянные расходы	Операционный расход на единицу техники
Станок 1	500 000	670
Станок 2	700 000	940

Рис. 8.3. Дерево решений Руководитель оценивает вероятность спроса на продукцию, производимую на станках:

• 2 000 ед. с вероятностью 0,4;
• 3 000 ед. с вероятностью 0,6.

Станок 1: 840 000 × 0,4 + 1 510 000 × 0,6 = 1 242 000. Станок 2: 1 180 000 × 0,4 + 2 120 000 × 0,6 = 1 744 000. Таким образом, приобретение второго станка более экономично. Недостатками дерева решений является ограниченное число вариантов решения проблемы. В процессе построения дерева решений необходимо обращать внимание на его размер. Оно не должно быть слишком перегруженным, т. к. это уменьшает способность к обобщению и способность давать верные ответы.

Источник

3. Оценка риска с применением теории полезности. Построение дерева решений. Функции полезности. Измерение отношения к риску. Пример. Оценка риска с применением теории полезности.

Существует несомненная связь между хозяйственным риском конкретных предприятий и личностными характеристиками лиц из числа руководства и специалистов предприятия, принимающих решения. Кроме того, успех в деятельности конкретного предприятия, представляющего на рынок определенные товары или услуги, в значительной степени зависит от правильности учета психологических особенностей потребителей, их отношения к риску — рисковать, или всячески страховать себя от возможных финансовых потерь, например, при покупке новых неизвестных товаров или услуг. Поэтому целесообразно рассмотреть различия в отношении людей к риску, хотя бы в финансовом отношении.

Для принятия оптимальных решений в условиях неопределенности и вызванного его риска с учетом отношения людей к риску используют элементы теории полезности.

Полезность отражает степень удовлетворения конкретного субъекта определенным товаром (изделием или услугой), а также действием. Использование полезности позволяет соизмерять вещи, которые физически являются несоизмеримыми, ее часто используют для ранжирования приоритетов при выборе.

Используя различные функции полезности, можно описать процедуры оценки конкретных экономических ситуаций через нахождение ожидаемого значения функции.

1. Из всего множества Х, предложенных экспертом значений определенного экономического показателя выделяют два значения X_* и X*, таким образом, что X ≥ X* (означает, что Х не хуже, чем X*, однако эксперт не делает между ними особой разницы) и X ≤ X* (означает, что X* не хуже, чем X, но эксперт не делает между ними особой разницы) для всех х ∈ Х. Таким образом получают два крайних значения шкалы X_* и X*.

2. Эксперту предлагают сравнить между собой два показателя: Xi и лотерею — получить X_* с вероятностью Р или X* с вероятностью (1-Р). Меняя величину Р, добиваются того, что значения Xi и лотерея L (X_*, X*, Р) станут, по мнению эксперта эквивалентными.

Фиксируют значение Xi и Рi для этой ситуации. Процесс повторяют меняя X i в интервале от X_* до X*.

3. Минимальному и максимальному значениям X_* и X* присваивают произвольные числовые значения полезности Umin=U(X_*) и Umax=U(X*), при этом соблюдают, чтобы Umax> Umin.

4. Полезность варианта определяется вероятностью U(x)=P(x), при которой человеку безразлично, что выбирать: гарантированный вариант или лотерею, см. выше п.2.

Например, в качестве функций полезности можно брать:

или

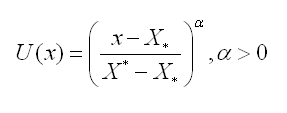
Первая, является растущей, вторая — убывающей.

Ожидаемое значение полезности ряда альтернативных результатов рассчитывается как средневзвешенное их полезностей по вероятностям.

Построение дерева решений.

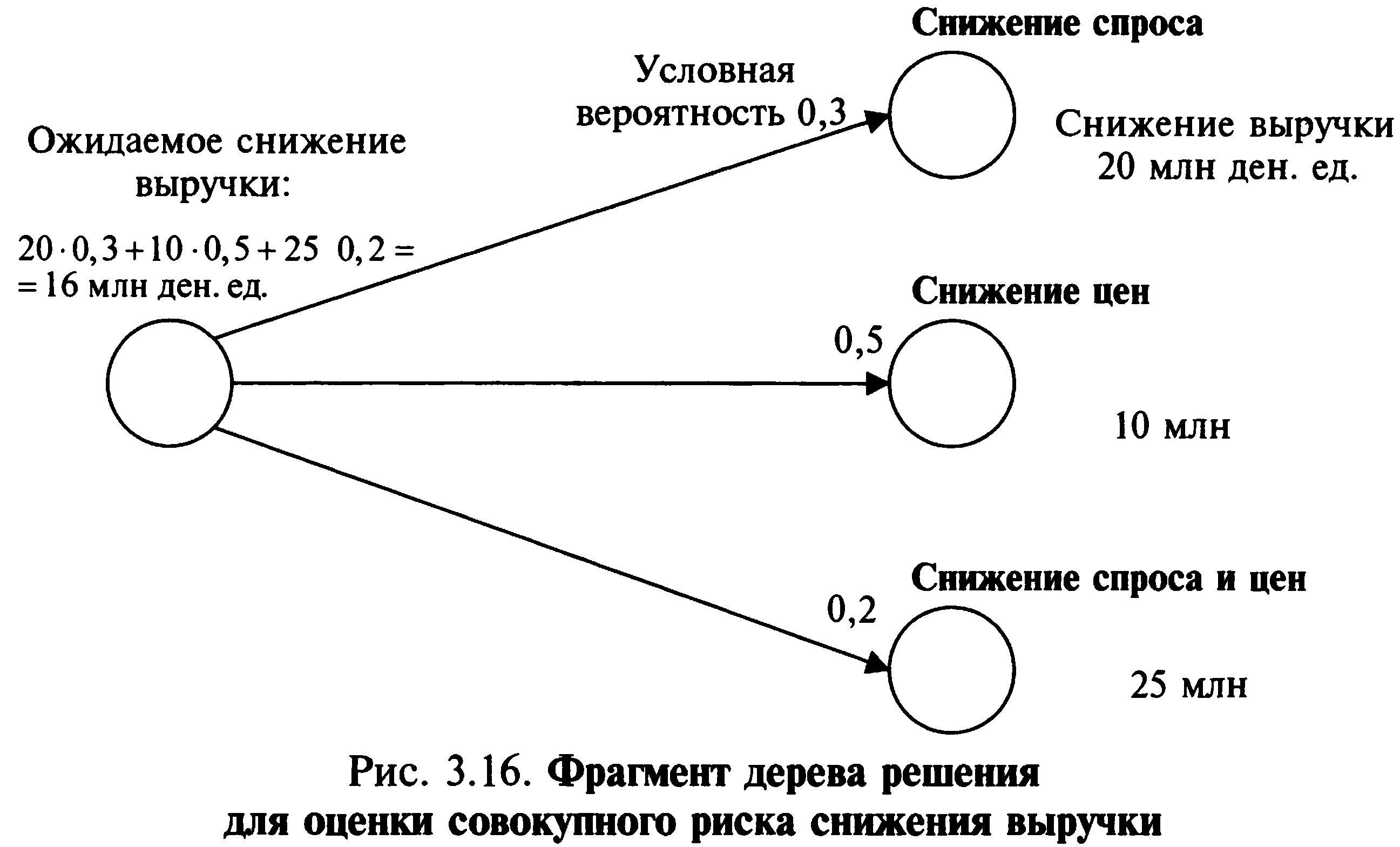
К важным инструментам исследования риска относится моделирование задачи выбора с помощью построения сложных распределений вероятностей (деревьев решений) — графического (сетевого) построения вариантов возможных решений. По ветвям дерева соотносят субъективные и объективные оценки возможных событий. Следуя вдоль построенных ветвей и используя специальные методики расчета вероятностей, оценивают каждый путь и выбирают менее рискованный. Последствия возникновения ситуации рассчитываются как произведение условной вероятности на оценку последствий. Пример построения дерева решений и оценка рисков на его основе представлены на рис. 3.16. Для непосредственного построения дерева решений часто используется метод сценариев («что, если. »). Дерево решений позволяет в графической форме изобразить причинно-следственную зависимость между рисковыми ситуациями и их последствиями, а затем по каждой группе альтернативных (взаимоисключающих и при этом одновременно возможных) событий определить условные вероятности и меры риска, что позволяет рассчитать усредненную оценку рисков. Таким образом формируется сценарий развития рисковых ситуаций (рис. 3.16).

Дерево решений позволяет провести анализ риска лишь в статике, что ограничивает применение этого метода.

Источник

Как увидеть лес за деревьями: что такое Decision Tree и зачем это нужно в Big Data

Продолжая насыщать курс Аналитика больших данных для руководителей важными понятиями системного анализа, сегодня мы рассмотрим, что такое дерево решений (Decision Tree). А также расскажем, как этот метод Data Mining и предиктивной аналитики используется в машинном обучении, экономике, менеджменте, бизнес-анализе и аналитике больших данных.

Как растут деревья решений: базовые основы

Начнем с определения: дерево решений – это математическая модель в виде графа, которая отображает точки принятия решений, предшествующие им события и последствия. Этот метод Data Mining широко используется в машинном обучении, позволяя решать задачи классификации и регрессии [1].

Аналитические модели в виде деревьев решений более вербализуемы, интерпретируемы и понятны человеку, чем другие методы Machine Learning, например, нейронные сети. Дополнительное достоинство Decision Tree – это быстрота за счет отсутствия этапа подготовки данных (Data Preparation), поскольку не нужно очищать и нормализовать датасет [2].

В бизнес-анализе, менеджменте и экономике Decision Tree – это отличный инструмент для наглядного отображения всех возможных альтернатив (сценариев), прогнозирования будущих событий, а также оценки их потенциальной выгоды и рисков. Для этого дерево решений представляют в виде графической схемы, чтобы его проще воспринимать и анализировать. Данный граф состоит из следующих элементов [3]:

• вершины, от которых возможно несколько вариантов, называют узлами. Они показывают возможные ситуации (точки принятия решений);
• конечные узлы (листья) представляют результат (значение целевой функции);
• ребра (ветви), соединяющие узлы, описывают вероятности развития событий по этому сценарию.

Обычно многоузловые деревья решений строятся с помощью специального программного обеспечения. Но граф с ограниченным числом вершин можно построить в табличном редакторе или даже вручную. Как это сделать самостоятельно, мы рассмотрим далее на простом примере из управленческой практики.

Строим дерево решений на примере обучения Big Data

Итак, проанализируем кейс построения дерева решений на примере расчета выгоды от обучения сотрудников новой Big Data технологии с целью быстрого выпуска продукта ценой X. При этом возможны следующие альтернативные сценарии:

• поручить каждому сотруднику самостоятельно освоить нужные подходы, фреймворки и языки программирования в свободное от работы время. Фактические затраты на реализацию такого решения равны нулю, а вероятность успешного освоения технологии для быстрого выпуска продукта оценивается на уровне 30%.
• выделить w рабочих дней на самостоятельное обучение каждого сотрудника на его рабочем месте. Фактические затраты на реализацию такого решения составляют стоимость рабочего дня каждого сотрудника в день (Z), умноженное на количество дней (w) и число сотрудников (k). Успех ожидается в 50% случаев.
• организовать корпоративное обучение всех сотрудников в специализированном учебном центре в течении n дней. Затраты на обучения составят совокупную стоимость курсов (Y), а также цену рабочего дня каждого сотрудника в день (Z)*количество дней (n)*число сотрудников (k). При этом сотрудники освоят технологию с вероятностью 98% за n дней (n

Затраты на реализацию решения

Вероятность успешного освоения технологии для быстрого выпуска продукта ценой X

Самостоятельное обучение каждого сотрудника вне работы

Самостоятельное обучение каждого сотрудника на работе

стоимость рабочего дня каждого сотрудника в день (Z)*количество дней (w)*число сотрудников (k)

Организованные курсы для всех сотрудников в учебном центре

цена обучения (Y) + стоимость рабочего дня каждого сотрудника в день (Z)*количество дней (n)*число сотрудников (k)

Сравнив в абсолютных числах выражения 0,3X, (X*0,5 – Z*w*k) и (X*0,98 – Y – Z*n*k), можно выбрать наиболее выгодный вариант. Таким образом, дерево решений позволяет количественно оценить риски, затраты и выгоды возможных альтернатив и выработать оптимальную управленческую стратегию. Не случайно профессиональный стандарт бизнес-аналитика, руководство BABOK, о котором мы рассказывали здесь, включило дерево решений в набор наиболее часто используемых техник [4]. В следующей статье мы расскажем, как деревья решений и другие методы интеллектуального анализа данных реализуются в новом тренде аналитики больших данных — Augmented Analytics.

Источник