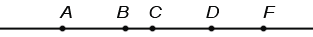Ответы дерево возможных вариантов
1 Методика изучения темы: « Элементы статистики, комбинаторики и теории вероятностей в школьном курсе математики 7- 9 классов»
Из опыта работы учителя математики МОУ – СОШ №5
Сливко Натальи Анатольевны
О необходимости изучения в школе элементов теории вероятностей и статистики речь идет очень давно. Приведу, например, цитату более чем столетней давности:
« Приходилось слышать, что теория сочетаний и бином Ньютона предлагаются иногда, как отделы, которые можно было сократить. Соглашусь на другие сокращения, выскажусь решительно против сокращения теории сочетаний. Теория эта по – особенному значению своему принадлежит к таким отделам, преподавание которых в гимназии следует непременно сохранить и поставить в лучшие условия. Теория сочетаний представляет средство для одной из важнейших способностей ума – способности представлять явления в разных комбинациях. Эта способность нужна в жизни всякому…». Так в 1899 году попечитель Московского учебного округа профессор П.А. Некрасов на совещании по вопросам средней школы описывал значение и место в школьном образовании того, что принято называть стохастической линией в преподавании математики.
По вопросам реформирования и модернизации нынешнего школьного математического образования существует множество весьма различных мнений. При этом среди вопросов о содержании школьной математики никто не подвергает сомнению необходимость включения стохастической линии в школьный курс, поскольку именно изучение и осмысление теории вероятностей и стохастических проблем развивает комбинаторное мышление, так нужное в нашем перенасыщенном информацией мире
Все мы довольно часто говорим «это невероятно», «более вероятно, что ..», « это мало вероятно», « можно утверждать со стопроцентной вероятностью, что …», когда пытаемся спрогнозировать наступление того или иного события. При этом мы опираемся на интуицию, жизненный опыт, здравый смысл и т. п. Но очень часто такие приблизительные оценки оказываются недостаточными: бывает важно знать, на сколько или во сколько раз совершение одного случайного события вероятнее другого. Иными словами, нужны точные количественные оценки, надо уметь численно характеризовать возможность наступления того или иного события. Раздел математики, посвященный исследованию количественных оценок случайных событий называется теорией вероятностей.
Её основателями считают Пьера Ферма и Блеза Паскаля. Эти французские ученые
17 века первыми нашли ключ к составлению количественной оценки вероятности события. Они использовали метод, который позже был назван комбинаторным анализом, или, проще, комбинаторикой.
Приведу пример, который иллюстрирует все вышесказанные слова.
Начальник написал 10 различных писем и поручил своему помощнику подписать 10 конвертов с нужными адресами. Тот так и сделал, но дальнейшее перепоручил секретарше. Она выполнила это ответственное задание формально, то есть разложила письма по конвертам, не обращая внимания на адреса. Какова вероятность
того, что ни одно письмо не попало в нужный конверт? Ответ оказывается на удивление большим: вероятность такой масштабной ошибки превышает 36%!
Раздел математики : «Элементы логики, комбинаторики, статистики и теории вероятностей» в школьный курс введен совсем недавно. Введение этих вопросов – веление времени. Для учителей этот раздел новый, все когда – то изучали эти вопросы в институте, но это было давно и учили нас, а теперь нам надо вспомнить
( можно сказать: выучить заново) и научить своих учеников.
Стохастическая линия в преподавании математики вводилась постепенно.
В 2002 — 2003 учебном году в курс алгебры 7 класса ввели тему «Элементы статистики», которая была рассчитана на 4 часа, и предлагалось ее изучать в конце учебного года за счет уроков повторения. В дальнейшем в 2003 – 2004 учебном году уже в 7 – 8 классах, а с 2004 – 2005 учебного года в 7 – 9 классах изучается тема
« Элементы статистики, комбинаторики и теории вероятностей». Рассмотрение этих вопросов также планировалось в конце учебного года, что было не очень удачным. Каждый учитель знает как трудно воспринимают дети новые темы в мае месяце.
В декабре 2007 года впервые в краевые диагностические работы были включены задачи по комбинаторике.( у меня не было тогда 9 класса).
В 2010 в апрельскую краевую диагностическую работу также включили задачи по комбинаторике ( 38% учащихся 9 «А» класса справились с решением этих задач). При проведении ГИА по алгебре в 9классах в 2010 году были включены задания по статистике и теории вероятностей. ( 84% учащихся 9 «А» верно выполнили эти задания)
В демоверсию ГИА по математике 9 класса 2011 года также входят такие задачи.
В 2010 – 2011 учебном году вопросы стохастической линии распределены следующим образом:
Источник
Комбинаторные задачи
Комбинаторика (от латинского слова combinare, означающего №соединять», «сочетать») — это область математики, которая изучает способы выбора, расположения, сочетания различных объектов. Решение задач в данном разделе математики требует рассмотрения и подсчёта всех возможных комбинаций (отсюда название комбинаторные задачи). Решая эти задачи, обычно надо отвечать на вопрос «Сколькими способами. » или «Сколько вариантов. «
Задача: Нам даны фигуры: треугольник, овал и прямоугольник . Необходимо построить пирамидку, состоящую из трех разных фигур. Сколькими способами это можно сделать?
Метод перебора
Данный метод удобен при небольшом числе вариантов. Решение в данном случае происходит путём перебора всех возможных вариантов. При этом очень важно выбрать правильный вариант перебора — логику перебора.
Воспользуемся методом перебора: Пусть в основании пирамидки находится прямоугольник, тогда возможны варианты построения: прямоугольник — овал — треугольник и прямоугольник — треугольник — овал.
Теперь в основании положим овал, тогда возможны варианты построения: овал — прямоугольник — треугольник и овал — треугольник — прямоугольник.
Теперь в основании положим треугольник, тогда возможны варианты построения: треугольник — прямоугольник — овал и треугольник — овал — прямоугольник.
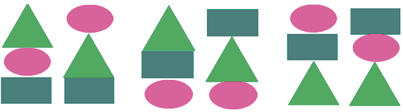
Итак, мы получили шесть возможных вариантов:
Ответ: 6 способов.
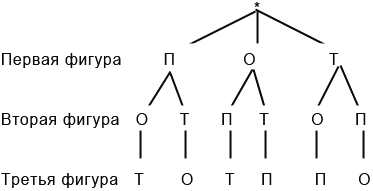
При решении данной задачи мы изображали фигуры, но для упрощения решения можно использовать кодирование. Данный прием позволяет заметить фигуры, например, первыми буквами их названия, то есть овал обозначаем буквой О, треугольник — Т, прямоугольник — П. Тогда решение будет выглядеть так:
Дерево возможных вариантов
Данный метод заключается в построении схемы, которая и называется деревом возможных вариантов. Данная схема действительно похожа на перевернутое дерево, «корень» которого обозначается «*». Построим данную схему для нашей задачи: Для этого от «корня» проведем три «ветки» — отрезки, на концах которых подпишем варианты фигур, которые мы можем взять за основание. Далее от каждой фигуры проводим такое количество «веток», которое будет соответствовать числу вариантов фигур на втором месте, в нашем случае по две «ветки» от каждой фигуры. Затем от каждой фигуры, стоящей на втором месте, проводим такое число «веток», которое будет соответствовать числу вариантов фигур на третьем месте, в нашем случае по одной «ветке» от каждой фигуры. Тогда имеем следующее дерево возможных вариантов:
Метод отрезков
Данный метод используется только для составления всевозможных пар. Например, рассмотрим прямую, на которой обозначены точки A, B, C, D, F:
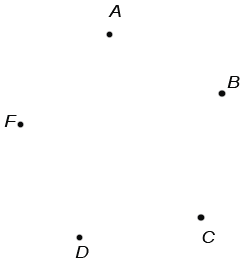
Необходимо ответить на вопрос: » Сколько отрезков изображено на рисунке?». Мы знаем, что отрезок обозначается двумя буквами, значит, для ответа на вопрос необходимо перебрать всевозможные пары букв. Это можно сделать при помощи следующей схемы: Отметим точки так, чтобы никакие 3 не лежали на одной прямой:
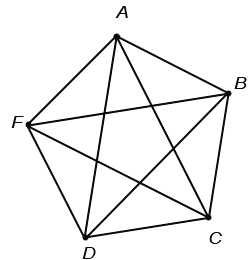
Соединим данные точки отрезками между собой. Число отрезков будет числом вариантов, то есть числом отрезков, изображенных на рисунке:
Итак, мы получили 10 отрезков, соединяющих точки.
Ответ: На рисунке 10 отрезков.
Источник
Комбинаторные задачи
методическая разработка по алгебре (8 класс) по теме
Размещения, сочетания, перестановки. Примеры и задачи с решениями.
Скачать:
| Вложение | Размер |
|---|---|
| | 312.5 КБ |
Предварительный просмотр:
Цель урока : познакомить учащихся с разделом математики – комбинаторикой. Показать решение некоторых комбинаторных задач.
Ход урока: объяснение материала; закрепление материала, решение задач.
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитать число комбинаций.
Такие задачи называются комбинаторными задачами, а раздел математики, в котором рассматриваются эти задачи, называется комбинаторикой.
Слово «комбинаторика» происходит от латинского слова combinate, которое означает «соединять», «сочетать».
На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром. Из скольких вариантов завтрака Вова может выбирать?
Всего вариантов столько же, сколько клеток в таблице.
Однако составлять такие таблицы для каждой задачи, занимает время.
А чтобы решить такую задачу быстрее, можно воспользоваться правилом умножения.
Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В , следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный.
Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?
Решение будем искать с помощью «дерева возможных вариантов».
Посмотрим на левую «веточку», идущую от «флага», пусть верхняя полоса – белого цвета, тогда средняя полоса может быть синей или красной, а нижняя – соответственно, красной или синей. Получилось два варианта цветов полос флага: белая, синяя, красная и белая, красная, синяя.
Пусть теперь верхняя полоса – синего цвета, это вторая «веточка».
Тогда средняя полоса может быть белой или красной, а нижняя — соответственно, красной или белой. Получилось еще два варианта цветов полос : синяя, белая, красная и синяя, красная, белая.
Аналогично рассматривается случай для верхней полосы красного цвета.
Получается еще два варианта: красная, белая, синяя и красная, синяя, белая.
Построенная схема действительно напоминает дерево, только перевернутое. Поэтому ее называют «деревом возможных вариантов» .
А вот так выглядит «дерево возможных вариантов» для такого примера 3 :
Сколько трехзначных чисел можно составить из цифр 1, 3, 5 и 7, используя в записи числа каждую из них не более одного раза?
Однако многие задачи можно решить быстрее и легче. Для этого надо знать простейшие комбинации, которые можно составлять из элементов конечного множества.
И одна из первых таких комбинаций — перестановки.
Имеются три книги. Обозначим их буквами a ,b и c.Эти книги нужно расставить на полке по-разному:
а b с, а с b, b а с, b с а, с а b, с b а .
Каждое из этих расположений и называют перестановкой из трех элементов.
Перестановкой из n элементов называют каждое расположение этих элементов в определенном порядке.
Обозначают : Р n = n! (эн факториал).
Поэтому задачу с книгами можно решить так:
Сколькими способами 4 человека могут разместиться на четырехместной скамейке?
Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из чисел 0,2, 4.6?
Решение: из цифр 0,2.4.6 можно составить Р 4 перестановок. Из этого числа нужно исключить те перестановки, которые начинаются с 0.
Число таких перестановок Р 3 . Значит искомое число четырехзначных чисел, которые можно составить из цифр 0,2,4,6 равно:
Р 4 – Р 3 = 4!-3!=
Имеются 9 различных книг, четыре из которых учебники. Сколькими способами можно расставить книги на полке так, чтобы все учебники стояли рядом?
Решение: сначала будем рассматривать учебники как одну книгу. Тогда на полке надо расставить не 9, а 6 книг. Это можно сделать Р 6 способами.
И в каждой из полученных комбинаций можно выполнить Р 4 перестановок учебников. Значит, искомое число способов расположения книг равно произведению: Р 6 *Р 4 =
В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно расставить расписание уроков на этот день так, чтобы два урока математики стояли рядом?
Вторым видом комбинаций являются размещения.
Пусть имеются 4 шара и 3 пустых ячейки. Обозначим шары буквами a, b, c, d. В пустые ячейки можно по-разному разместить три шара из этого набора .
Источник